基于混合包围盒与三角形相交的碰撞检测优化算法

孙敬荣，卢新明

1.山东科技大学，山东 青岛 266590

2.山东科技大学 山东省智慧矿山信息技术省级重点实验室，山东 青岛 266590

1 引言

碰撞检测（Collision Detection，CD）是虚拟网络游戏、物理仿真[1]、虚拟仿真技术[2]、机器人技术[3]、数控加工等的关键技术。现阶段在碰撞检测领域的研究方法主要有：基于物体空间的碰撞检测算法和图像空间的碰撞检测算法[4]。层次包围盒是一类经典的碰撞检测算法，同时三角形相交检测也是一类在碰撞检测中应用广泛的算法。随着虚拟现实应用内容的复杂化以及应用领域的日益扩大，应用环境的实时性以及复杂性对碰撞干涉检测的要求越来越高，单一的基于层次包围盒或传统三角形相交已经很难满足人们对碰撞检测准确性与速度的需求。并且，近几年国内外对三角形相交测试的研究十分的活跃，但基本都过度重视了算法的速度，而忽视了稳定性。该研究旨在通过结合并优化包围盒算法与三角形相交算法以保证碰撞检测的速度与准确性。

2 算法原理

基于对碰撞检测的研究，将碰撞干涉检测分为预处理检测和详细检测两阶段，在预处理阶段，将待测空间均匀划分，然后算法基于混合层次包围盒树，对处在同一网格区域内的相邻对象构造混合层次包围盒树。当两个待测物体的AABB-OBB混合层次包围盒树建成后，通过遍历两棵混合包围盒树，进行包围盒之间的相交测试：当两个包围盒未相交时，该节点停止检测；当包围盒相交时，对该节点的子节点进行检测；当叶节点包围盒相交时，则转入详细检测，在详细检测阶段，针对传统三角形相交算法过度追求速度而稳定性不足的特点，对算法进行了优化改进，其流程图如图1所示。

图1 碰撞检测流程图

2.1 预处理检测阶段

预处理阶段经过对空间的均分确定了相邻对象，然后只对相邻的对象构造AABB-OBB混合层次包围盒，常用的包围盒有以下几种：轴向包围盒（Axis-Aligned Bounding Box，AABB）[5]、方向包围盒（Oriented Bounding Box，OBB）[6]、k-DOPs和Sphere-OBB[7]等，其中AABB的优势在于构造简单，相交测试的更加简单速度，它直接将三维的相交运算转化为一维上的6次比较运算，只要在3个坐标轴上的投影均相交，则判定两个物体发生碰撞。但其紧密性不足，需要构造的层数较多，增加了计算量。而OBB紧密性更好，甚至一度视为碰撞检测算法的重要标准，它优势在于包围盒方向，可以根据待测物体的形状尽可能包围该物体，但这使得OBB的构造过程更为复杂，所以采用了AABB-OBB混合包围层次盒，其总体性能优于其他包围盒。

2.1.1 AABB-OBB混合包围盒构造的优化

针对OBB包围盒，构造算法进行了优化，在此之前Gottschalk等人已经提出了一种通过计算三角形网格的方法来构建几何多面体的OBB包围盒。他将三角形的顶点集合看成3个变量的概率分布函数，再通过计算均值和协方差矩阵的特征向量来计算OBB包围盒的位置与方向[8]。其中设包围盒中三角形个数为n，xi、yi、zi为第i个三角形的3个顶点。则有：

三角形各个顶点的均值为：

协方差为：

通过计算可以得出矩阵C的特征向量并将其单位化，同时，由于C的特征向量是相互垂直的，即方向轴，然后将各点投影到方向轴上，确定包围盒的大小，但这种构造方法当三角形基本元不均匀时，包围盒整体会偏向基本元尺寸较小且密集的部分，可能会造成包围盒与待测物体偏差过大，使得包围紧密性变差。为了提高检查的效率与准确性，对原有算法进行优化，选择三角面片的面积为权值，给各个三角形进行加权，即设三角形面积为S，则：

物体的表面积为：

各个三角面片的中心为：

则协方差矩阵为：

通过这种方法可以看作两个包围盒中的一个是否完全在另一个的外边，除去第一层AABB外，下层的OBB包围盒的检测利用了Gottschalk等基于分离轴定理提出的检测方法，如果它们之间存在着一条分离轴，则判定它们未相交的。

2.1.2 AABB-OBB混合层次包围盒树的优化

预处理检测的核心在于遍历两个待测对象的混合层次包围盒树，将遍历过程定义一个任务树，各项任务为各个节点间的碰撞检测，所以只需要对任务树进行单重遍历即可完成对两棵树的同步深度优先遍历，同层的子任务之间为或的关系，若其中一个子任务检测结果为相交，则两个包围盒碰撞。

基于二叉树的思想，第一层采用AABB，下层都采用了OBB，因为AABB的结构相较于其他包围盒是最简单，通过第一层的检测，快速排除大量的无关信息，接下来通过下层的OBB进一步检测处理，采用OBB可以更加紧密的包围待测物体，减少相交检测的层数，同时对任务树结构进行优化，只对每一层相交的数据进行存储，然后下边的每一层对上一层存储信息构造包围盒进行碰撞检测，形成如图2所示的结构。预处理检测具体步骤如下：

步骤1通过空间剖分，对空间内相邻的两个对象的根节点A和B进行碰撞检测。检测根节点的两个AABB是否相交，若未发生相交，则直接判定未发生碰撞，否则进入步骤2。

步骤2若A和B均为枝节点，同时并行进行4个子任务，即A、B同时向左，A向左B向右，A向右B向左，AB同时向右的4种并行的相交测试，如果以上4种都未发生相交，则判定未发生碰撞，否则进入步骤3；

若A为叶节点、B为枝节点，或者A为枝节点、B为叶节点，并行进行AB同时向左和向右相交测试两个子任务，如果以上两种都未发生相交，则直接判定未发生碰撞，否则进入步骤3；

若A和B均为叶节点，则转入详细检测，即对三角形基本元进行相交测试，如果相交，则判定发生了碰撞并返回碰撞的详细信息，否则判定两个对象之间并未发生碰撞。

步骤3把之前相交的节点重新标记为A和B，然后返回步骤2。

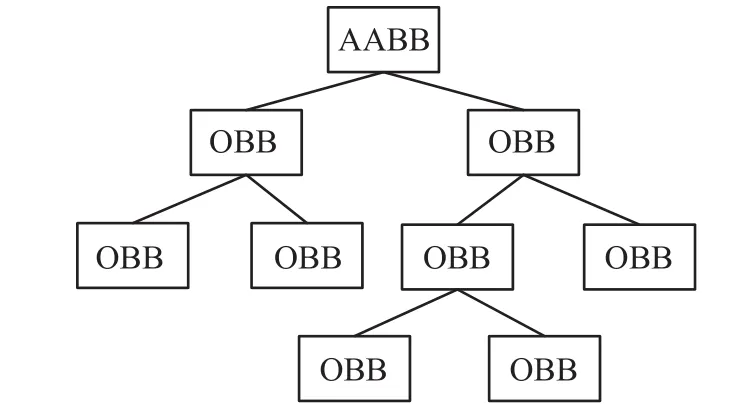
图2 AABB-OBB结构图

2.2 碰撞检测的详细检测

碰撞检测的根本即简单几何形状之间的关系测试。高效的三角形对相交测试对于提高碰撞检测算法速度和准确性以及增强虚拟场景的展现起至关重要的作用[9]。目前，矢量判别型算法和标量判别型算法是针对三角形快速相交检测的两种主要算法。其中矢量判别法主要是通过三角形各个顶点构成的行列式，然后行列式的正负几何意义来判断两个三角形的点、线、面之间的相对位置关系，进而判断两个三角形是否相交[10]；而标量判别算法核心思想是通过准确向量计算来判断两个三角形之间相交关系，标量判别算法典型的有Möller[11]、Trop[12]算法。本文提出的详细检测是在Möller算法基础上，加入坐标系变换而提出了一种优化算法，通过坐标变换求得新的计算坐标系，在新的计算坐标系下进行向量之间的运算，在保证检测准确性的前提下，提高了检测速度。

2.2.1构建计算坐标系

针对待测三角形，需要构造新的计算坐标系，使得其中的一个待测三角形在新的坐标系平面上。设三角形A的P0、P1、P2顶点已经给出，构建基于这个三角形的计算坐标系O*，如图3所示，然后通过以下三步形成以P0为原点，以及n0、n1、n2为单位向量的计算坐标系O*。

图3 构造计算坐标系

P0P1的单位向量为：

新旧两个坐标系之间的坐标变换矩阵为：

其中根据计算坐标系原点P0求出参数d0、d1、d2的值：

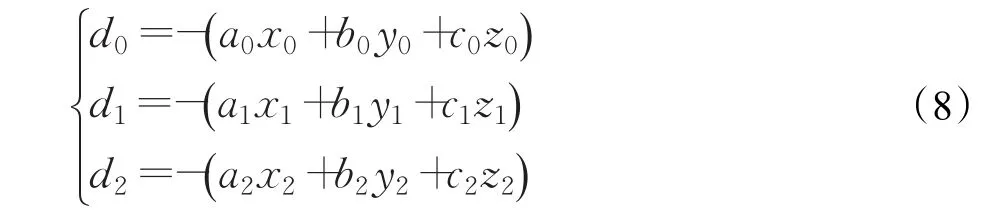
2.2.2 计算坐标系下的优化检测算法

根据Möller算法原理，设两个三角形A和B所在的平面分别为ΠA、ΠB。如果三角形A、B分别与平面ΠA、ΠB平面相交于LA、LB，则LA、LB必定在两平面ΠA、ΠB的交线L上；若LA、LB有重叠部分，则两三角形相交，否则判定为相离。通过求出B的顶点与A所在平面ΠA之间的距离以及A的顶点与B所在平面ΠB之间的距离，通过距离关系快速的排除基本元集合中不相交的三角形。但Möller算法需要建立各个三角形所在的平面，计算时需要2次“求交”，这样无法保证检测的速度。

在算法相交判断原理的基础上进行优化，基于投影降低纬度的方式，通过引入新的计算坐标系，在新坐标系下简化了运算，原本空间中三角形的运算转化为二维平面问题，这样能更容易判定两个三角形的“相交”或者“不相交”的状态。通过投影，在新计算坐标系的xy以及xz面，求取三角形A、B顶点的正投影，然后在判断两个三角形投影关系时将三角形相交检测分为共面与异面两种情况，在新坐标系下进行边向量之间的运算，通过向量运算的结果判断三角形基本元之间的相交情况。

（1）判断A与ΠB的是否存在交线段LA

从图4可知，三角形A与ΠB的交线LA(P0P1)在H面上(z=0)。空间直线可以通过两个点用参数式表示为：由A与Av所形成的梯形A0'A1'A1A0可以得到，P′0在A0'A1'上的参数t0'跟P0在A0A1上的参数t0相等；同理P0'在A0'A2'上的参数t1'跟P1在A0A2上的参数t1相等。而且P0'与P1'都有z=0，y=0，那么只需要判断x即可。

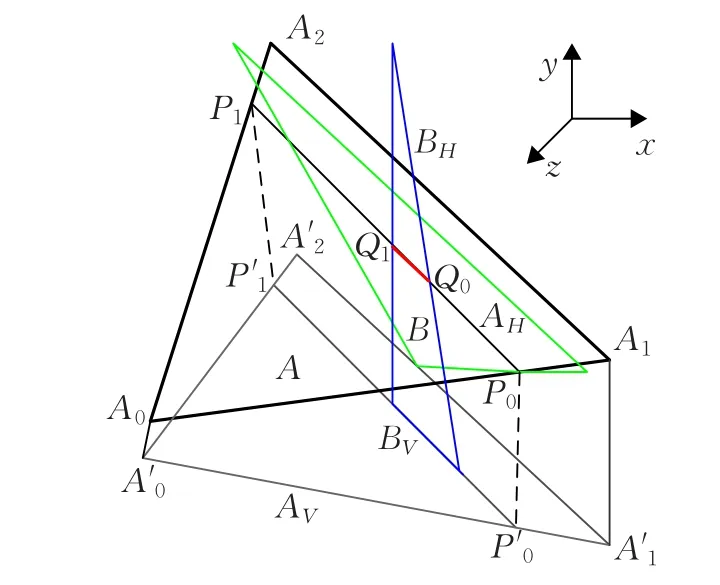
图4 坐标系下两三角形相交计算

（2）判断LA在B内的部分是否存在交线

在V面上求直线 Av与Bv交点与及其对应的参数t，然后在H面上判断0，如果或者 Q0=Q1，则两个三角形碰撞。

算法伪代码判断流程描述如下：

输入：第k层中A，B两物体所包含的三角形Ai和Bj。

输出：0未碰撞；1碰撞。

if（三角形B与平面H平行）

{

判定 A与 B是共面，goto（1）；

判定A与B是异面的，即A与B未相交，返回0；

}

else

{

if（AVandBV存在交点）

{

if(Q0Q1=φ)

A与B未相交，返回0；

if（Q0=Q1）

A与B相交，返回1；

if（Q0Q1与BH的某条边重叠）

A与B相交，返回1；

}

else

A与B未相交，返回0；

}

当A与B共面时，则判断AH与BH两个三角形位置关系的伪代码如下：

if（AH与BH是相离的）

A与B未相交，返回0；

if（AH与BH是重叠的）

A与B相交，返回1；

if（AH与BH存在一个相交点）A与B相交，返回1；

if（AH与BH存在一条相交线）

A与B未相交，返回0；

详细检测阶段算法除坐标系的转换外，其他算法均为二维平面上的运算，为了加速运算，在算法中加入拒绝判定，达到快速判断Av与Bv是否相离目的。即在新的计算坐标系的z方向，如果在Av上的3个z坐标的符号相同，那么表明Av在Bv的上方或下方，则两者是分离的，即两个三角形未发生碰撞。

3 算法测试与分析

实验是在CPU I5-2450M 2.50 GHz，内存4 GB，独立显卡1 GB环境，应用VB6.0的笔记本上实现。实验完成2个对象相互碰撞的情况，对象由3dt格式（山东蓝光软件有限公司）的三角形基本元组成。在测试时插入2个定时计算器，记录碰撞检测时间，然后在相同的环境下分别应用文献[5-6，13]中的算法进行了碰撞检测，对比这几种算法在相同的情况下得到相同正确的检测结果所需的时间。提高及实验场景的复杂度，三角形对数随着场景复杂度的增加而增加，重复的进行上述实验，总共10组实验，实验结果如表1所示，算法效率对比如图5所示。

通过表1与图5可以发现，在三角形重叠数目相同时，在预处理阶段提出的算法相比文献[6]、[7]、[8]中提出的算法，碰撞检测的时间明显缩短。

在详细检测时，算法计算量的多少决定了算法运行的速度，算法中包括加减、乘除、比较以及绝对值等运算，将以上几种运算所需要运行的时间看作是相同，则算法的计算量可以看作是几种运算相加的总和。通过与经典的Möller、Tropp算法以及文献[14]、[15]、[16]等提出的算法对比，各算法计算量的对比如表2所示。

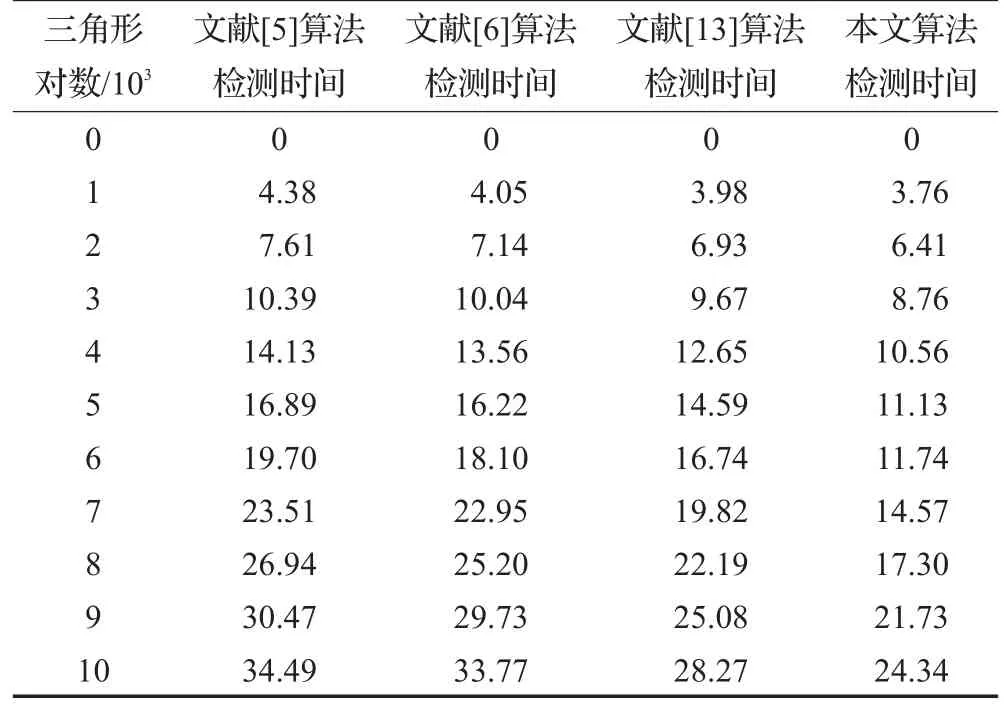
表1 算法检测时间对比表 ms

图5 算法检测时间对比图

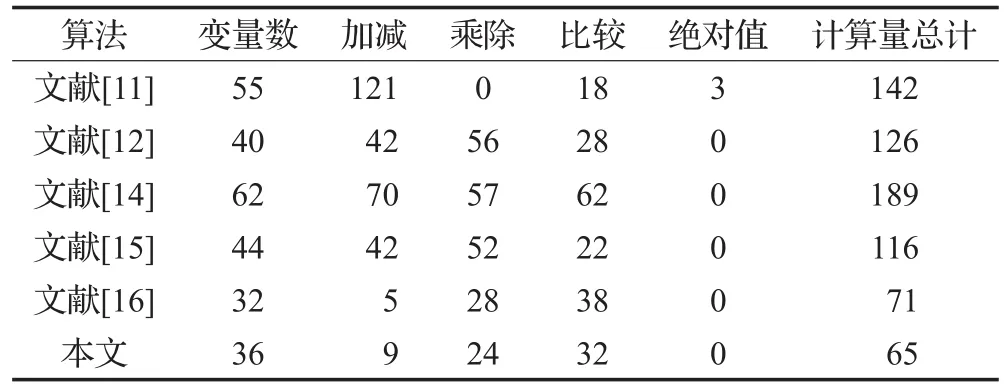
表2 不同算法间计算量的比较

尽管计算坐标系的变换在本算法中占用了一定的时间份额，但经过综合的测试分析后，本算法坐标系变换的开销利大于弊，通过表2可以发现该算法的计算量要小于其他算法，即改进算法检测效率优于其他算法。最后进行算法的实际性能检测：

测试内容为待测物体分别应用本文算法以及文献[11]和[15]提出的算法进行检测，进行时间与准确性进行对比，其中每次测试的预处理检测阶段均采用了该文提出的算法；测试是在lionking平台（山东蓝光软件有限公司）进行，图6为测试场景，圆圈内为相交区域。测试在相同的条件下进行，每组重复测试5次求取平均值。

实验结果如表3所示，详细检测阶段的三角形相交检测保证了检测的准确性，而且通过整体的时间对比可以发现，相比较其他两个算法，本文提出的算法在保证碰撞检测准确性的前提下检测速度大幅提高。

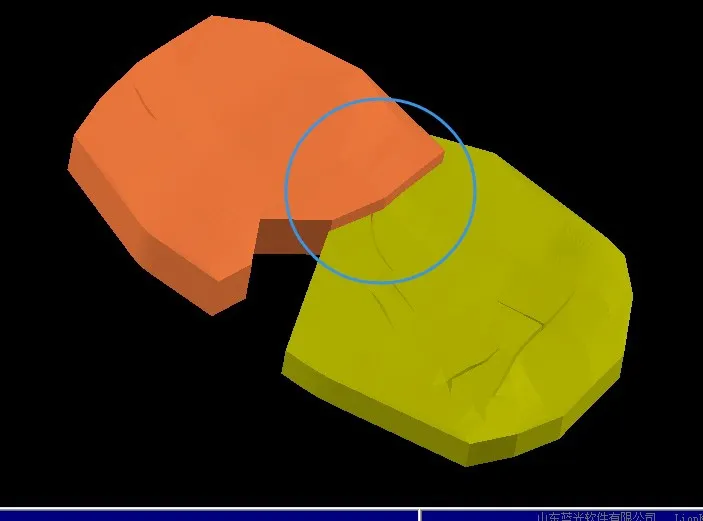
图6 待测物体测试场景

表3 不同算法的时间与准确性对比

4 结束语

现阶段，快速、准确的碰撞干涉检测是虚拟现实领域的研究热点，本文提出一种基于混合层次包围盒与三角形相交相结合的混合碰撞检测算法。混合层次包围盒结合了AABB和OBB各自的优势，同时优化任务树，提高了遍历的速度。然后在新坐标系下的向量计算的算法相比其他算法，在保证了检测的准确性的前提下提高了碰撞检测的速度。然而任何碰撞检测算法都不可能适用于各种各样的场景，在应对包含对象较少的场景时，该算法没有显著的优势，而更适合用于较为复杂且包含对象较多的场景。下一步，将研究涉及奇异性三角形基本元的相交检测。