基于云存储的隐式加密算法改进

崔 蕾,邵天会

(烟台职业学院,山东 烟台 264670)

随着数据的重要性日益增强,数据安全越发得到人们的重视,大数据云存储安全的重要性不言而喻,在针对云存储数据加密方式中,隐式加密因为不需要秘钥,并且在保证安全性同时提高了加密解密效率,从而得到广泛应用,目前比较好的隐式加密算法(K,K)和(K,N)数据存储方式,这两种加密方式的改进不乏优秀的算法,但是往往保证了安全性却损失了加密效率,改进分割数据的处理方式是提高效率和保证数据安全性的关键环节。

1 基于隐式加密算法的问题

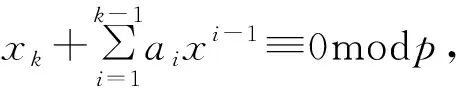
2 改进的隐式加密算法

改进的加密方案主要在数据分割阶段,首先将数据分割为等长度的N部分ri,将每个ri分割为K块,再进行(K,N)操作，把K块进行映射为N,其中K<=N,即(r1,r2,…rk)映射到集合(d1,d2,…dk),如图1所示。

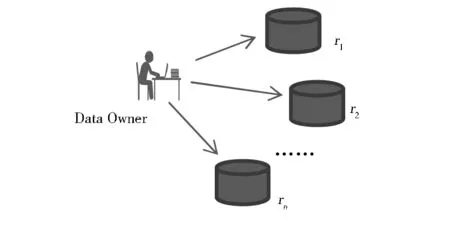
图1 数据平均分割模块图

因此对每个ri进行二次分割后构成(r11,r12,…r1k),(r21,r22,…r2k),…(rn1,rn2,…rnk),如图2所示。

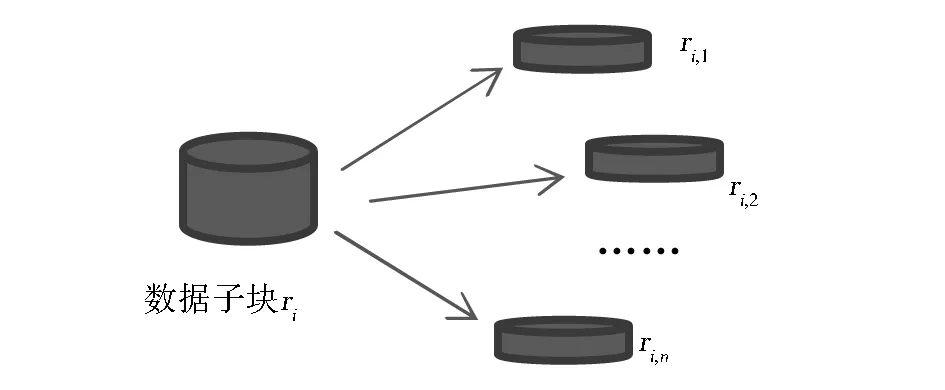
图2 数据子块分割模型图

因为每个ri为等长的N,因此每个rik可以构成N个线性方程:

b11r11+b12r12+…+b1kr1k=e11

b21r11+b22r12+…+b2kr1k=e12

…

bn1r11+bn2r12+…+bnkr1k=e1n

其中bij是数域P中任意值,并且生成N个数据。

同理：

b11ri1+b12ri2+…+b1krik=ei1

b21ri1+b22ri2+…+b2krik=ei2

…

bn1ri1+bn2ri2+…+bnkrik=ein

存储数据时对数据N冗余存储操作,线性方程组表示为矩阵形式b*r=e:

我们从矩阵b中任意选取k*k方阵,不难得出系数b(k*k)矩阵是可逆的,令b系数不全为0,目前b和r中一列相关,为了加强关联性,b*r*b=e′(e′为新生成的矩阵),保证e和b,r中的每个行列值都相关,因此增强了数据的关联性,增加数据的安全性。因为b(k*k)是可逆的,恢复数据r我们需要把其中的任意的k个数据进行如下操作r=b-1*e′*b-1:

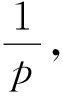
3 算法部分案例化

在分割数据阶段可以借鉴MapReduce原理,构造map函数[4],对数据进行中间值的提取,对中间值进行算法的二次分割,也就是进行2次map操作,得到的数据结果我们终止reduce操作,提取Map数据结果进行改进的算法的运算,这样提高了数据分割的效率,并且适应于大数据的操作,但是对于小数据来说,开销没有减少。

利用5个服务器进行操作,其中4个用于存储数据,1个用来算法的执行,四份数据被分成x1,x2,x3,x4,y1,y2,y3,y4,z1,z2,z3,z4,d1,d2,d3,d4,同时把四份数据定为x=x1x2x3x4,y=y1y2y3y4,z=z1z2z3z4,d=d1d2d3d4,数据x,y,z,d分别存放在4个服务器中,负责计算的服务器进行m=x*y*z*dmodp,n=(x+y+z+d)modp,k=(xy+xz+xd+yz+yd+zd)modp,j=(xyz+xyd+yzd+xzd)modp操作,其中p为大素数。

计算过程中每个服务器都进行四个方程的模运算,例如计算j=(xyz+xyd+yzd+xzd)modp操作:

第一步:

1)server1计算w1=x1y1z1+x1y1d1+y1z1d1+x1z1d1,得到随机数n1,将n1*w1,得到结果s1=n1*w1,n1x1y1z1,n1x1y1d1,n1y1z1d1,n1x1z1d1发到server5;

2)server2计算w2=x2y2z2+x2y2d2+y2z2d2+x2z2d2,得到随机数n2,将n2*w2,得到结果s2=n2*w2,n2x2y2z2,n2x2y2d2,n2y2z2d2,n2x2z2d2发到server5;

3)同理分别在server3、server4计算w3,w4,得到随机数n3,将n3*w3,n4*w4,得到s3,s4,发送到server5。

第二步:服务器server5进行计算操作

1)s1*s2*s3*s4=n1w1n2w2n3w3n4w4相乘运算;

2)将server1、server2、server3、server4发送到server5的数据进行乘积运算;

3)用1)减2)各项的和,得到s;

4)server5把结果s分成4份,r1,r2,r3,r4,并且满足s=r1*r2*r3*r4,然后将r1发到server1,r2发到server2,r3发到server3,r4发到server4。

第三步:server1、server2、server3、server4分别计算r1/n1,r2/n2,r3/n3,r4/n4r4/n4,然后计算四个数的乘积,显然得出(r1/n1)(r2/n2)(r3/n3)(r4/n4)=(r1*r2*r3*r4)/(n1*n2*n3*n4)=s/(n1*n2*n3*n4)=xyz+xyd+yzd+xzd。

同理进行其他的运算。

4 算法仿真实验分析

本实验硬件环境采用4台主机作为存储服务器,4台主机配置相同,CPU为i7-7740X,主频4.3Ghz,内存16G,内核数为4,线程为8,1台主机作为计算机服务器, CPU为i7-7800X,主频3.5Ghz(最高为4.0Ghz),内存16G,内核数为6,线程为12,1台主机作为攻击服务器,配置和计算机服务器相同。软件环境操作系统采用win10、JDK1.8环境配置,开发工具Eclipse4.7.0,使用JAVA语言开发,根据MapReduce原理构造新的map函数,应用在4台存储服务器上,在计算服务器上对改进的隐式加密算法进行数据的计算。

从数据库中抽取记录数为870的记录集,对记录集进行不同k,n值(2,3),(3,3),(2,4)的数据分块,并对分块后的数据进行改进的隐式加密算法运算,p取值3,攻击服务器对其中的2、3、4台存储服务器进行数据窃取还原,不同的k,n取值进行足够多次数的数据窃取还原操作,通过结果分析得出折线图3。

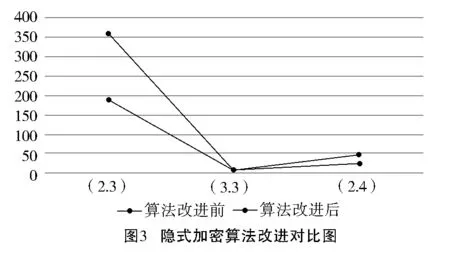
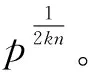
安全性分析,只要负责存储的四个服务器不同时进行合谋,其他的任何服务器之间合谋都不能够产生数据的泄露,即使负责运算的服务器和其中的3个负责存储的服务器进行合谋也无法获得正确的数据。计算量分析,运算在简单的加法和乘法中进行,没有对数、乘方等复杂运算,运算的时间得到了保证。算法没有进行加密操作,因此没有密钥的产生,无需保存密钥,同时也没有产生加密字典,各个数据在不同的服务器存储,数据进行二次分割后并且进行了N冗余数据处理,每个数据的获取难度增加到P的指数级,同时我们在进行计算中没有复杂的乘方等运算，从而提高了运算的速度,我们引进了MapReduce思想进行分割数据,使整个算法的效率得到提高。