基于二叉树存储结构的LZW改进算法

崔方送

(安徽黄梅戏艺术职业学院,安徽 安庆 246052)

引言

随着大数据时代的到来,面对海量的数据信息,为了进行传输和存储,必须对其进行压缩。在数据压缩过程中,我们通常接收的是一些未知统计特性的信息,为了对这些数据信息进行压缩,自适应的普适编码方法就应运而生,其中LZ系列算法是其中一个重要分支。在1977年,以色列科学家Ziv和Lempel提出了该算法[1],并在1978年提出了一种改进算法,这两种算法也就是后来所称的LZ77算法和LZ78算法[2]。在这之后,一些专家学者提出了很多改进算法,其中最有影响的是Terry Welch在1984年提出的Lempel-Ziv-Welch算法,即LZW算法[3]。

1 LZW算法

1.1 LZW算法简介

LZW算法是一种基于字典的编码方法,它继承了LZ77和LZ78算法的优点,容易被人们所接受[4]。所谓基于字典的方法就是将字典中的词条的编码代替被压缩数据中的相应的字符串。很显然,被压缩信息中各词条出现的频率越高压缩效果越好。

1.2 LZW算法基本原理

在LZW算法编码过程中[5-6],编码器逐个读入字符,并累积成一个字符串C,每输入一个字符就被串接在C后面,然后在字典中查找C,若在字典中能找到C,就重复此过程,直到在某一点,添加下一个字符x使搜索不成功,即字符串C在字典中,而Cx不在字典中,此时就输出字符串C在字典中的编码,并将Cx作为新的词条存储到字典的相应位置,同时将字符串C预置为x。

在LZW译码过程中,需要根据码字,逐步重新建立字典,其过程与编码相同,这是译码算法的关键。

1.3 LZW算法存在的问题

LZW算法是一种自适应算法,字典的词条是在编码过程中逐渐建立的,在压缩开始时,字典的词条数目和每个词条的长度是无法量化的,而且该算法会受内存容量、算法复杂度和计算速度等因素的限制,所以在编码过程中,当字典的条目很多、词条的长度较长时,即存储字典所需的内存空间超过了计算机的内存,编码效率明显下降以及计算机运行缓慢。因此,本文提出了改进算法。

2 LZW算法改进

2.1 改进思想和原理

针对LZW算法的不足,在编码译码过程中,我们应尽量减少字典对内存的开销,本文采取以下方法以优化存储过程。首先编写文件转换算法,将待压缩文件按每个字符8位二进制数转换成二进制文件，即‘0’、‘1’字符串,然后只需对该二进制文件进行LZW编码,编码过程中字典的存储方式采用二叉树结构进行存储,二进制文件中‘0’和‘1’分别和二叉树节点的左右孩子域相对应。二叉树节点结构如图1所示。

图1 二叉树节点结构

为了查找方便,本文采用二叉树的一种主要存储结构,即采用三叉链表节点结构,图1中,Index表示该节点编码,Parent指向该节点的父母节点。对该结构进行初始化如图2所示。

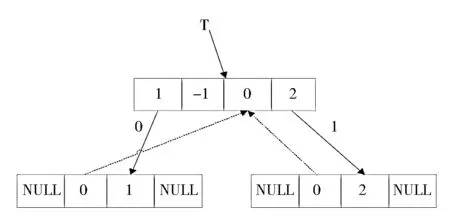
图2 初始化二叉树

图2中,T为二叉树指针,指向二叉树的首节点,首节点中Parent域赋值为-1,表示不指向任何节点,Index域赋值为0,表示首节点的编码为0,Lchild域指向编码为1的节点,Rchild域指向编码为2的节点,同时,节点1和节点2的Parent域指向首节点,表示节点1和节点2的父母节点都是首节点。在该结构中,‘0’和‘1’表示编码过程中读入的二进制字符,当读入的是‘0’且需要将新词条存储到字典中时,就将该词条插入到相应节点的Lchild域,当读入的是‘1’且需要将新词条存储到字典中时,就将该词条插入到相应节点的Rchild域。

2.2 改进算法的具体实现

2.2.1编码算法[7]

步骤1:将待压缩文件按每个字符8位二进制的形式转换成二进制文件，即‘0’、‘1’字符串;

步骤2:初始化二叉树T,树中包含所有的根，即包含词条‘0’和‘1’,且将当前前缀赋值为空即C=NULL;

步骤3:从二进制文件读入字符x,并C=C+x;

步骤4:若所读文件为空转步骤6,否则读入下一字符x;

步骤5: 查找C+x是否在二叉树中,若在,就将字符x连接到字符串C尾部，即C=Cx,转步骤4,若不在,输出字符串C的编码,并将字符x插到字符串C编码节点的左孩子域或右孩子域,并置C为x,转步骤4;

步骤6:结束。

编码算法流程图如图3所示。

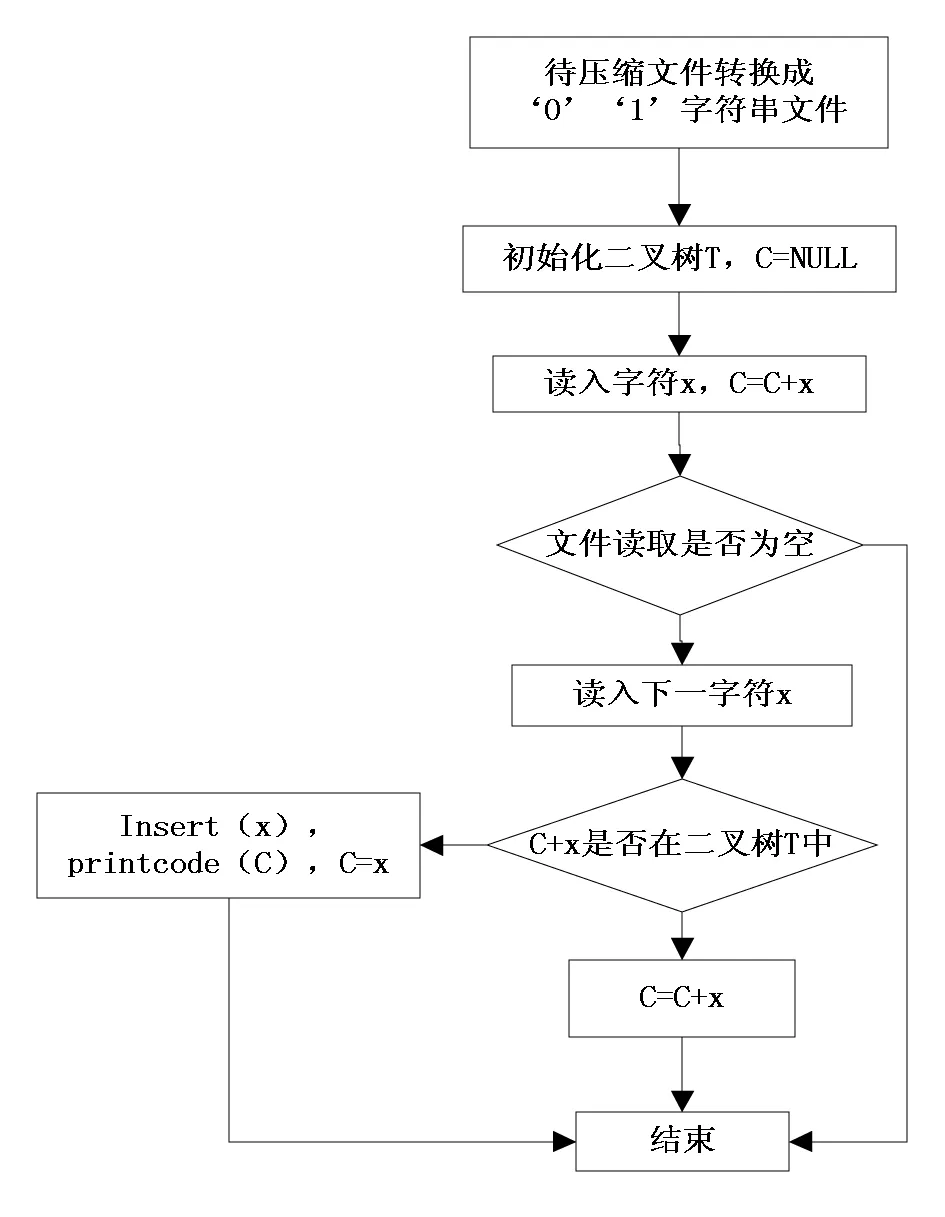
图3 编码算法流程图

2.2.2译码算法

步骤1:初始化二叉树T,树中包含所有的根，即包含词条‘0’和‘1’;

步骤2:读取码字cw,并输出cw在T中对应的字符串 Findstr(cw);

步骤3:前缀码字pw=cw;

步骤4:继续读下一码字cw,;

步骤5:判断Findstr(cw)是否在树T中

若在,输出Findstr(cw),P=Findstr(pw),C为Findstr(cw)的首字符,Insert(P+C);

若不在,P=Findstr(pw),C为Findstr(pw)的首字符,输出P+C,Insert(P+C);

步骤6:判断译码文件是否为空,若是转步骤3;

步骤7:将所得二进制文件转换成相应的字符文件;

步骤8:结束。

2.3 算法字典存储空间分析

此处以二进制字符串“1110010110010101”为例进行编码、译码分析[8]。图4是编码过程中二叉树字典结构。

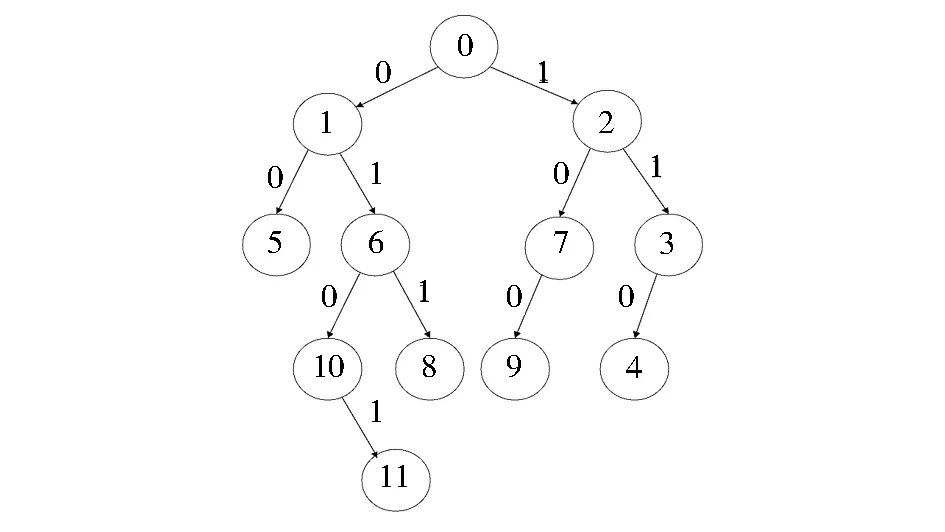
图4 编码过程中字典结构

对字符串“1110010110010101”编码后输出的码子为2,3,1,1,2,6,7,6,10,2。图3中,节点中的数字代表相应字符串的编码,节点间的二进制代表从二进制文件中读入的二进制字符串。如果读入的是‘0’且需要插入词条,就插在相应节点的左孩子域；若读入的是字符‘1’且需要插入词条,就插在相应节点的右孩子域。

该二叉树字典中存储空间分析:节点1代表的是字符串“0”,节点6代表的是字符串“01”,节点10代表的是字符串“010”,节点11代表的是字符串“0101”,显然,在插入节点6时,只需在节点1的右孩子域插入即可;在插入节点10时,只需在节点6的左孩子域插入即可;在插入节点11时,只需在节点10的右孩子域插入即可。可以看出,词条“0”“01”“010”“0101”只用了4个节点就可以存储,这里的“0”“01”“010”都没有重复存储,当二叉树的深度越深时,节点代表的字符串越长,此时可节省大量的存储空间,从而有效克服原LZW算法字典存储的不足。

3 算法测试

根据改进算法,对不同大小的文本文件做了仿真测试,结果如表1所示。

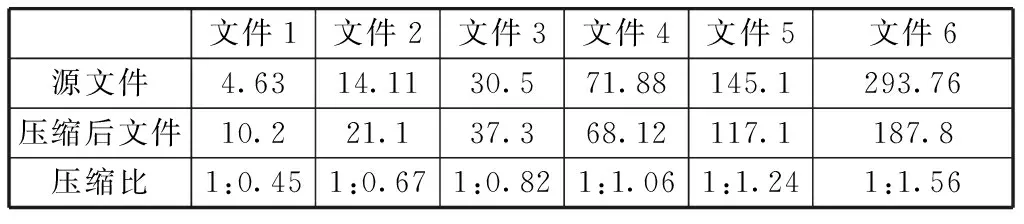
表1 改进算法和原算法压缩效果比较(单位:KB)

从表1中可以看出,随着文件大小的增大,压缩效果越来越明显。当文件比较小时,该压缩算法起不到压缩效果,如文件1、文件2和文件3,这是因为当文件比较小时,文件中重复的词条较少,字典中的词条相对较多且词条不长,同时转换成二进制字符串文件后,文件增大,压缩率大于1。随着文件的增大,文件中重复的词条较多,字典中词条比较长,尽管一个字符被转换成8位二进制字符串后,压缩率仍然小于1。

4 总结

LZW算法是一种有效的自适应数据压缩算法,本文在此基础上,主要从如下两方面做了一些改进:一方面,将待压缩文件转换成二进制文件再进行LZW压缩,这样实现该算法简单方便;另一方面,采取二叉树结构来存储编码过程中字典的词条,以便减少字典中词条内容的重复存储,从而减轻算法运行中内存的压力。本文改进算法对LZW算法的字典存储提供了新的研究思路,对数据压缩算法的研究有一定参考价值和现实意义,但还存在一些有待解决的问题。