装配式混凝土楼板在人群荷载下的激励研究

张谊平

(河南质量工程职业学院,河南 平顶山 467000)

引言

随着建筑技术和计算分析的发展,传统建筑结构工业化水平较低、周期长、高投入、高消耗、高污染等已经明显不适应社会的发展。然而目前发展的装配式建筑能够满足低碳、绿色环保,可以很好地缩短施工周期,生产效率高、施工周期短,在推进建筑产业化的转型中而被大力推广[1-2]。但是针对于装配式混凝土的大跨度结构楼盖系统更轻、更柔,频率和阻尼都比较低,人群行走、跳跃、有节奏运动及机器运行时频率比较接近结构的自振频率,从而使结构更容易在这些作用下产生共振,楼盖竖向加速度和速度加大。过大的动力响应会导致使用者的不舒适,产生心理恐慌;生产厂房楼盖振动过大,则会影响产品的加工精度和工艺系统的正常运行。

舒适度问题是基于满足结构正常使用极限状态功能要求的一部分,楼盖系统的振动,一般不会对结构安全造成影响,但是却会让居住者感到烦恼和不安,给人的身心健康造成不良影响。因此,结构设计之初就必须对舒适度问题给予充分的考虑,否则一旦结构建成以后再进行处理就会非常困难,造价也会大大增加。近年来,大量新建建筑物中过大的楼盖振动问题已经引起了广泛的关注。装配式楼板应用于大跨度结构其可以做到施工速度快,但是相比于传统的楼板较轻柔,所以还需要对该种装配式楼板进行舒适度研究。

1 人群激励曲线

导致楼板振动的因素主要是行走激励源,一般由单人连续行走、跑动、跳跃,或者由多人共同活动引起的。行走激励影响结构响应的因素主要有人行走速度、人数、体重、行走步距及相位等。选取适当的行走激励荷载模型来模拟行走激励是楼板振动舒适度性能研究的基础。因此本文只是研究了单人行走和5人行走以及定向激励跳跃工况下的楼板舒适度。

1.1 单人落足激励模型

行走激励是一个比较复杂的随机过程。首先要研究单足落步的荷载曲线,继而研究连续行走、竖向跳跃的激励模型。Bishop[3]和Ellingwood[4]研究了人在楼板和楼梯上走动引起的振动,通过大量的试验得到了人行走时竖向力与时间的典型的名义单步落足曲线如图1所示。图中纵坐标代表竖向接触力与人体重的比值。单步落足曲线呈M形,中点O表示由于足跟逐渐接触地面,由于人体重心的转移而对地面的接触力逐渐增大,曲线高度达到1.2时,出现峰值点A,随后反力开始减小,直至点B(约为0.67),接着人的脚掌蹬地,随着屈膝、摆动另一只脚和重心的转移,使得曲线再次升高至点C(约1.15),过点C以后,曲线迅速下降至点D,此时人的足尖完全脱离地面。这条曲线是目前应用最广泛的时程曲线,本文采用单足落步曲线来模拟不同行走路线对楼板的激励。

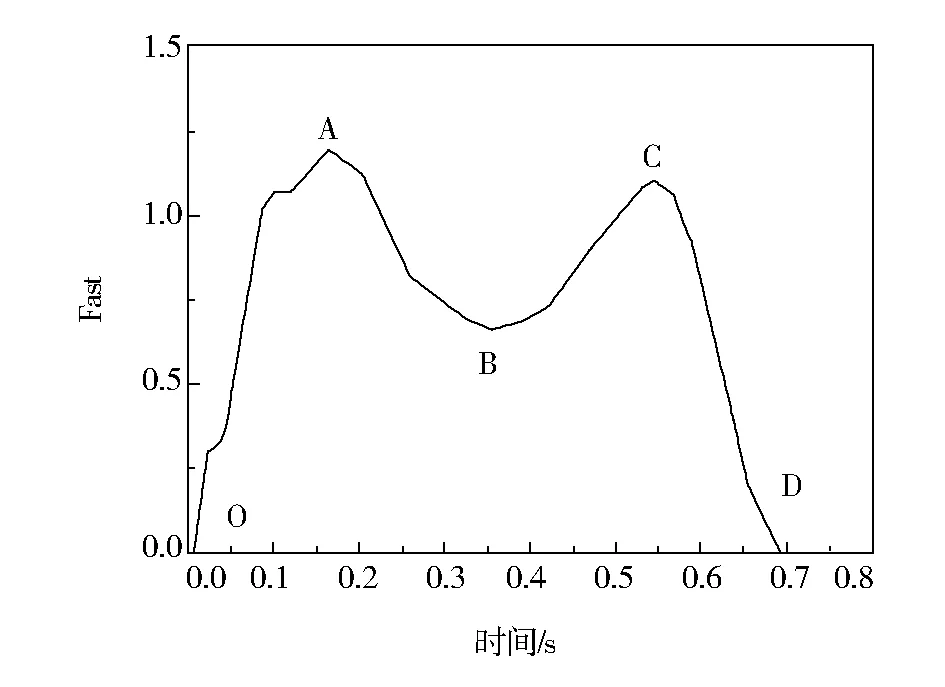
图1 单足落步曲线

1.2 连续行走激励模型

假定人的左右足单足落步曲线完全一致,就可以得出连续的行走激励时程曲线如图2所示。行走频率和行走速度对连续行走时程曲线有很大的影响,人的行走频率一般在1.4 Hz-2.5 Hz之间,行走速度为0.9 m/s-1.8 m/s。美国钢结构学会推荐采用的常规步频为1.8Hz-2.2Hz。

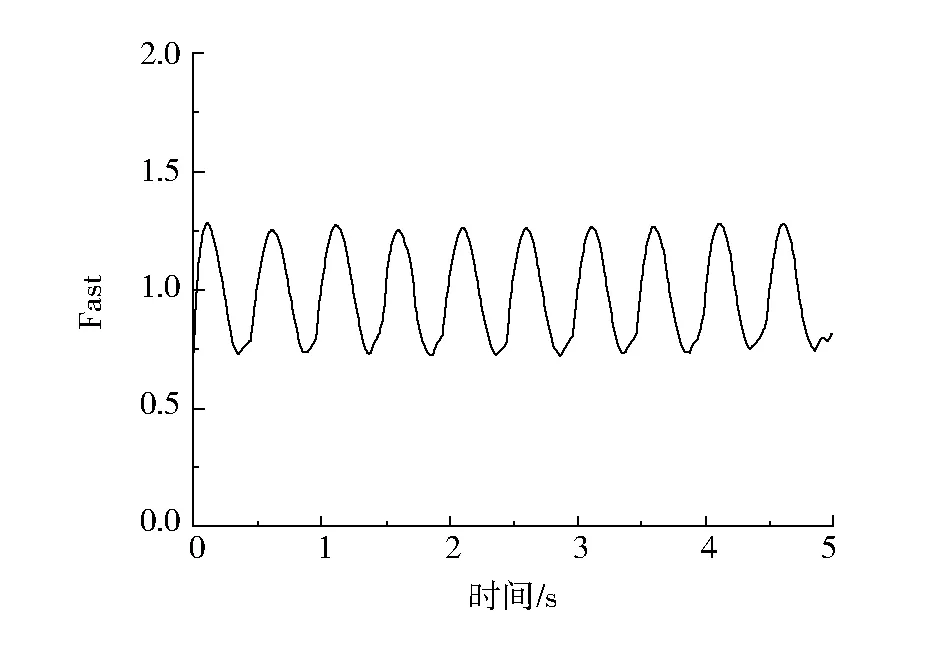
图2 连续行走时程曲线

1.3 竖向跳跃激励模型

人在楼盖上进行跳跃活动的时候,对楼盖的作用力是不连续的,如果我们要采用一个函数来模拟这种作用力时,这个函数需要有两个阶段:一是人的脚底面与楼盖接触的时间段,这个阶段是人对楼盖施加荷载的时间段;二是人跳离楼盖,由于人体与楼盖没有接触,故对其作用力为零。天津大学于敬海等对此做了一定的研究[5],得出下面的函数表达式:

F(t)=0tp≤t≤T

(1)

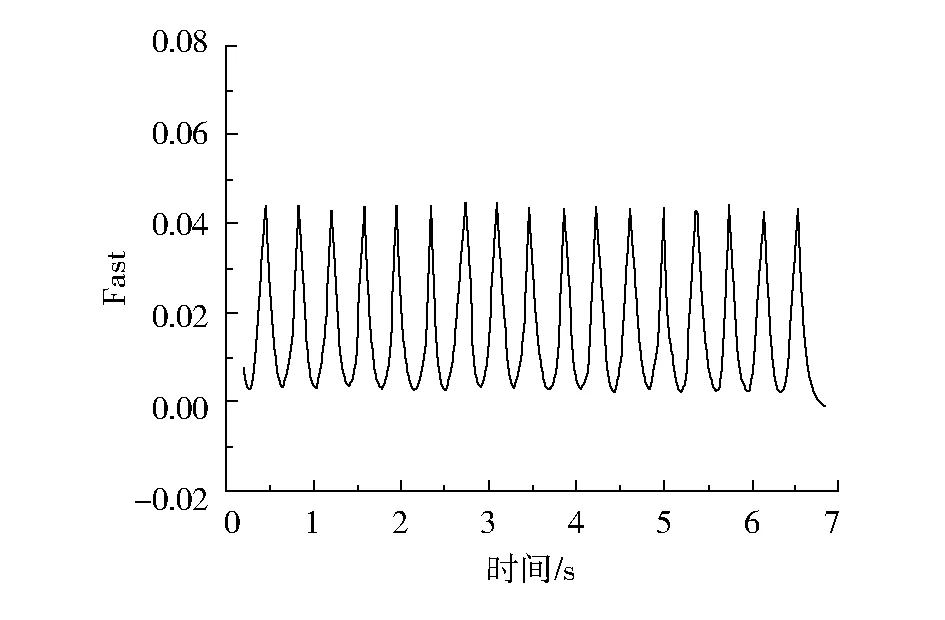
图3 3.0 Hz跳跃激励曲线

2 测点布置与分析工况

本次舒适度试验采用的楼盖为2层楼盖,平面尺寸为24 m×24 m。将拾振器底部用防水胶带包裹,用橡皮泥粘在混凝土楼板上。根据模态分析情况,测点选择对振动敏感的区域,为研究楼盖竖向振动加速度衰减情况,选取三条路线,采用5个测点,编号为1、2、3、4、5,分布如图4所示。

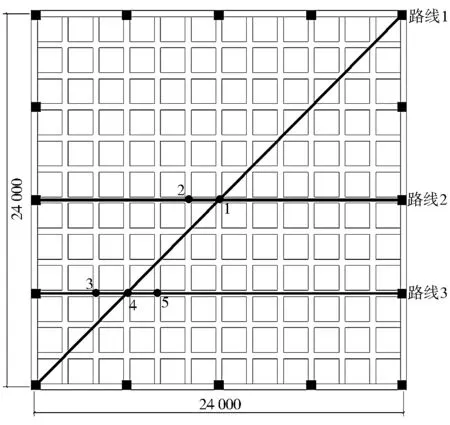
图4 行走路线以及测点布置图

试验开始前,在混凝土楼板上根据步距用粉笔画若干道横线作为标记,要求测试者根据既定频率按固定步距行走,本次参加测试五人体重P1-P5分别为80 kg、75 kg、75 kg、69 kg、67 kg。分析工况分为人行激励类工况和定点激励类工况:

2.1 人行激励类工况

工况一～三:考虑单人行走路线。如图4中路线1、路线2、路线3分别为沿跨度方向、沿纵向及沿斜向行走。步行频率为2 Hz,步距0.75 m,P2体重75 kg,通行时间分别为42 s、15 s、20 s。工况四～五:考虑五人行走路线,五人齐步行走,步行频率为2 Hz,步距0.75 m,通行时间分别为42 s、14 s。工况六～七:单人跑动路线,纵向跑动。跑动速度4.5 m/s,步距1.4 m,通行时间分别为14 s、7.8 s。工况八～九:五人跑动路线,考虑五人跑动路线,工况八为五人齐步沿着路线2和3跑动,工况九为五人齐步沿着路线1跑动,跑动速度4.5 m/s,步距1.4 m,通行时间分别为14 s、7.8 s。

2.2 定点激励类工况

工况十:单人P2体重75 kg,在测点1处原地踏步,持续时间10 s。工况十一:单人体重70 kg,在测点1处跳跃,持续时间10 s。工况十二:五人在测点1附近同时跳跃。

3 结果分析

3.1 自振振型

自振特性分析时,质量源取来自1倍恒载+0.5倍活载,楼盖的自振振型选取前六阶进行分析,由于计算模型对称,理论上第二、三阶振型应该相等,第四、五阶振型也应该相等,但是由于在划分网格的时候,网格和节点并不对称,因此有一定的差距,但是相差不大。装配式楼盖的前六阶振型如图5所示。由图5可以看出，该种楼盖的低阶振型主要以竖向振动为主,类似于相同支承条件下的实心平板,而在进行定点激励时候选取的激励点(低阶振型中心)即是楼盖的几何中心,该点的竖向振动响应最大,最容易发生共振。

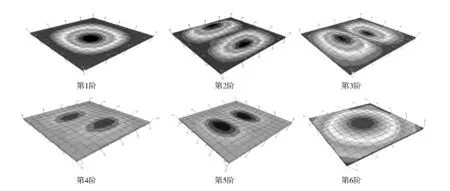
图5 装配式楼盖前六阶振型

3.2 十二种工况作用下各测点加速度峰值

利用布置在楼盖上的拾振器记录下在人行荷载和跳跃激励工况下加速度反应,楼盖实测竖向振动加速度峰值如表1所示。

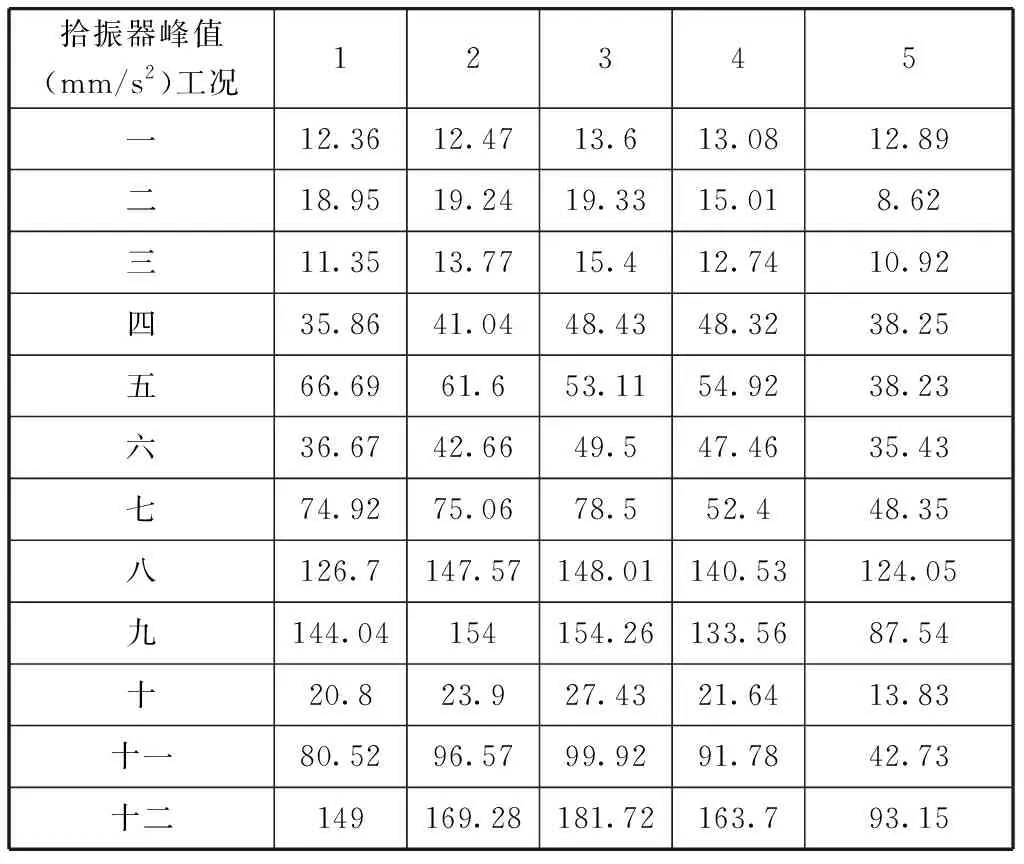
表1 楼盖实测加速度峰值

由表1可知,总体上测点1、2、3的加速度峰值大于测点4、5的峰值,其中以测点3的峰值最大。根据有限元分析,测点3位于一阶振型最大点处,因此其峰值加速度也最大。根据行走路线和上表可知,当行走路线经过测点中心时,峰值加速度较大,当行走路线偏离行走中心时,其峰值加速度较小,并且行走路线偏离测点的距离越远,其峰值加速度越小。

大跨度钢结构玻璃采光顶造型美观、施工进度快、周期短、现场焊接量减少近一半；可以减少施工现场阶段对构件的测控工作，减少对焊缝的检测量，在加工厂焊接，可提高焊接质量及精度，在一些大型商业区、医院、车站等公共建筑中具有广泛的推广空间。

3.3 人行激励类

人行激励类采用行走路线法对楼盖进行加速度时程分析,考虑行人在装配式楼盖上直线行走,根据行走的频率和步距,计算出不同点处到达的时间,然后在行走路线上各点施加单步落足激励曲线作为节点动力荷载进行时程分析,得出各测点在人行激励下竖向加速度时程曲线与试验结果进行比较,以验证试验结果的正确性,由于限于本文的篇幅只列出工况一、工况四、工况六、工况八的分析结果。

3.3.1工况一

工况一作用下1点-5点加速度时程曲线如图6所示。

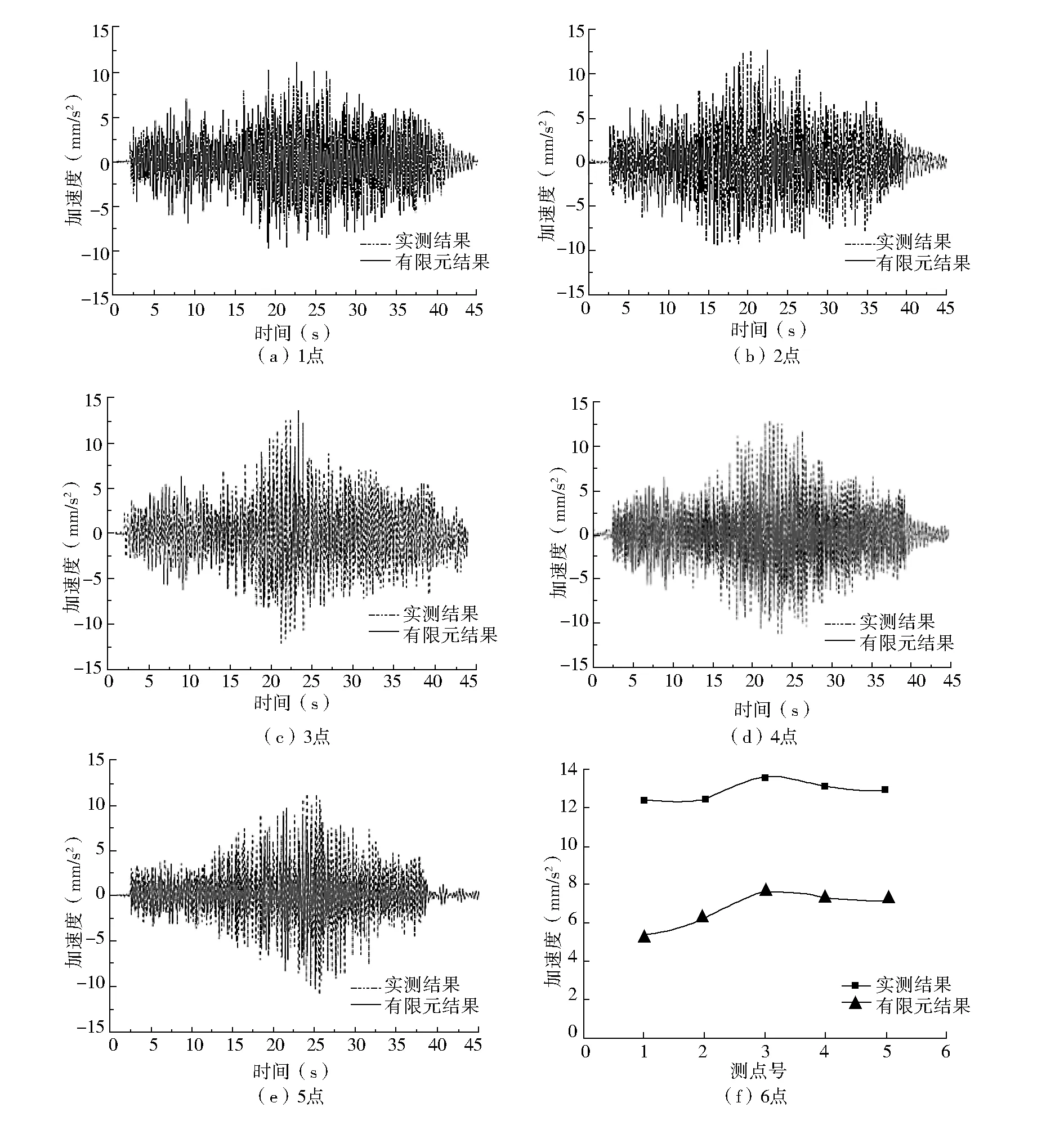
图6 工况一各测点加速度时程曲线及峰值曲线

由图6可以看出,测点3为一阶振幅最大点,其加速度峰值出现在总行走持时的一半左右,即装配式楼盖一阶振幅最大点峰值加速度响应与单人行走路线无关。不同的行走路线引起的加速度峰值不同。由各测点峰值加速度曲线可知,沿纵向行走引起的加速度峰值最大,其次是沿斜向和跨度方向。行走路线一(以工况一为例)通过第3、4、5点,其引起的测点峰值加速度3点最大,但与第4、5点相差不大。有限元计算时程曲线与实测时程曲线趋势吻合较好,但最大加速度略小于实测结果,这是由于环境振动与人行激励叠加从而使峰值加速度增大。

3.3.2工况四

工况四作用下1点-5点加速度时程曲线如图7所示。

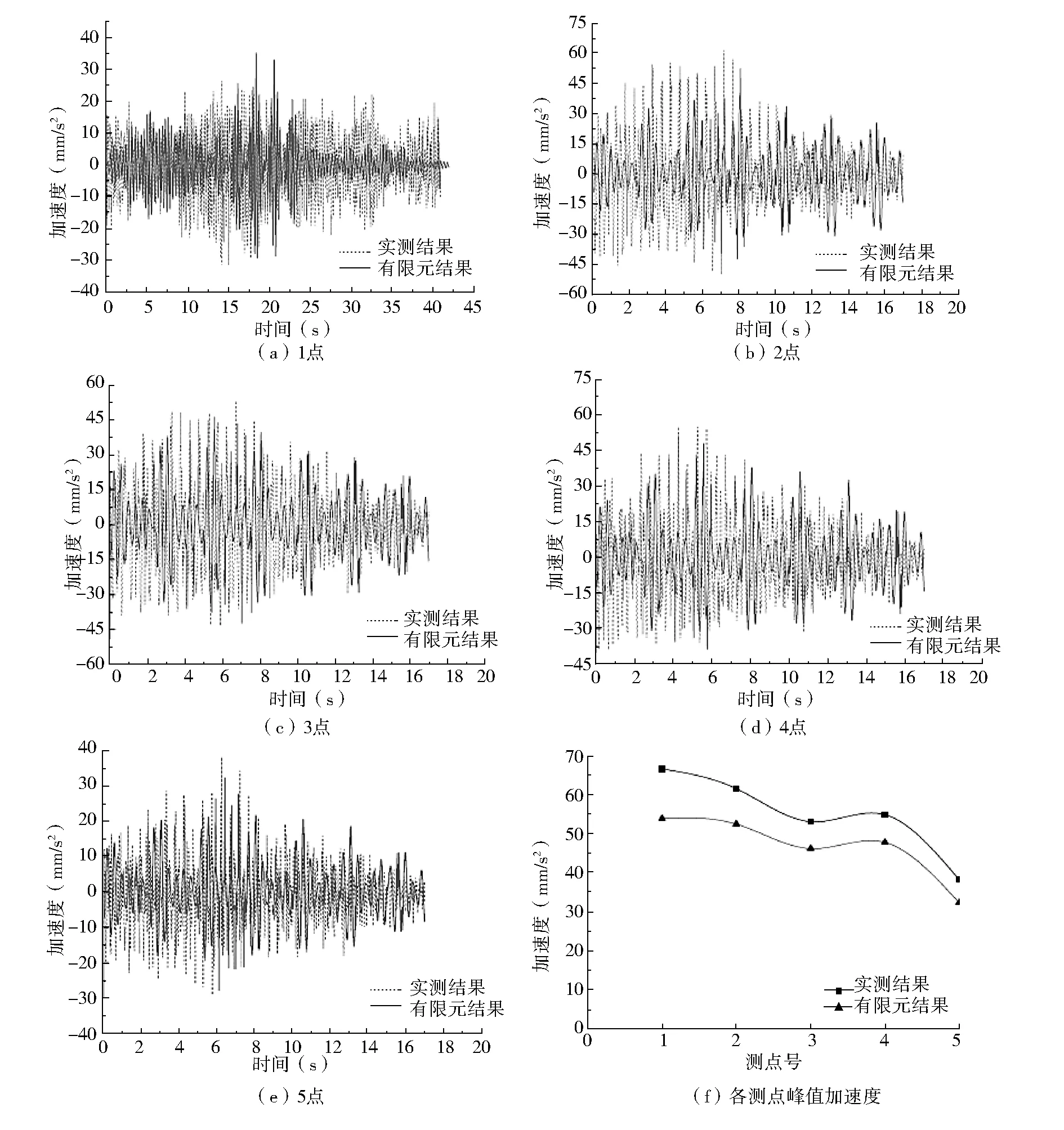
图7 工况四各测点加速度时程曲线及峰值曲线

图7为工况四各测点加速度时程曲线及峰值曲线,其五人行走路线为沿跨度方向,其实测加速度时程曲线与有限元分析加速度时程曲线吻合较好,加速度峰值基本处于行走时间中间处,行走路线上各测点加速度峰值明显大于偏离行走路线各测点加速度峰值。实测结果大于有限元计算结果,但其峰值为66.69 mm/s2,远小于美国ATC指南(227 mm/s2)及《高规》(203 mm/s2)规定的限值。

3.3.3工况六

工况六作用下1点-5点加速度时程曲线如图8所示。

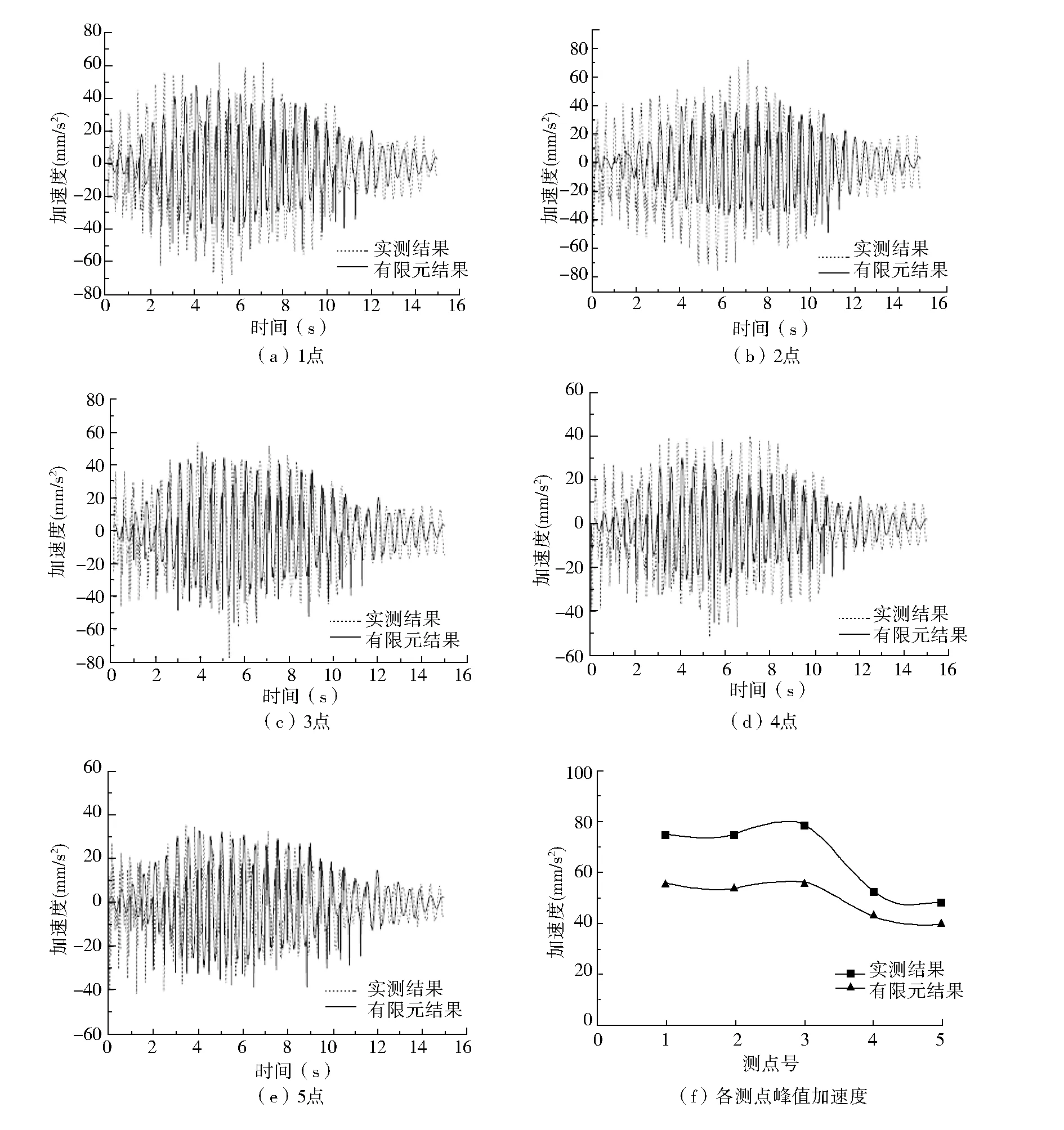
图8 工况六各测点加速度时程曲线及峰值曲线

图8为工况六(沿跨度方向单人跑动)各测点加速度时程曲线及峰值曲线。实测加速度时程曲线与有限元分析加速度时程曲线吻合较好,加速度峰值基本处于行走时间1/2处,跑动路线上各测点加速度峰值明显大于偏离行走路线各测点加速度峰值实测结果,大于有限元计算结果,其峰值为78.46 mm/s2,约为单人行走加速度峰值的四倍,但仍远小于美国ATC指南(227 mm/s2)及《高规(203 mm/s2)规定的限值。

3.3.4工况八

工况八作用下1点-5点加速度时程曲线如图9所示。

图9为工况八(五人沿跨度方向单人跑动)各测点加速度时程曲线及峰值曲线。实测加速度时程曲线与有限元分析加速度时程曲线吻合较好,加速度峰值基本处于行走时间1/2处,除测点5外,沿纵向跑动产生的峰值加速度大于沿跨度方向跑动产生的峰值加速度,测点五由于靠近中柱,附近楼盖刚度较大,峰值加速度明显小于其他测点加速度。实测结果大于有限元计算结果,其峰值为148.6 mm/s2,约为单人行走加速度峰值的1.9倍,也明显大于单人、多人行走及单人跑动等工况,仍小于美国ATC指南(227 mm/s2)及《高规》(203 mm/s2)规定的限值。

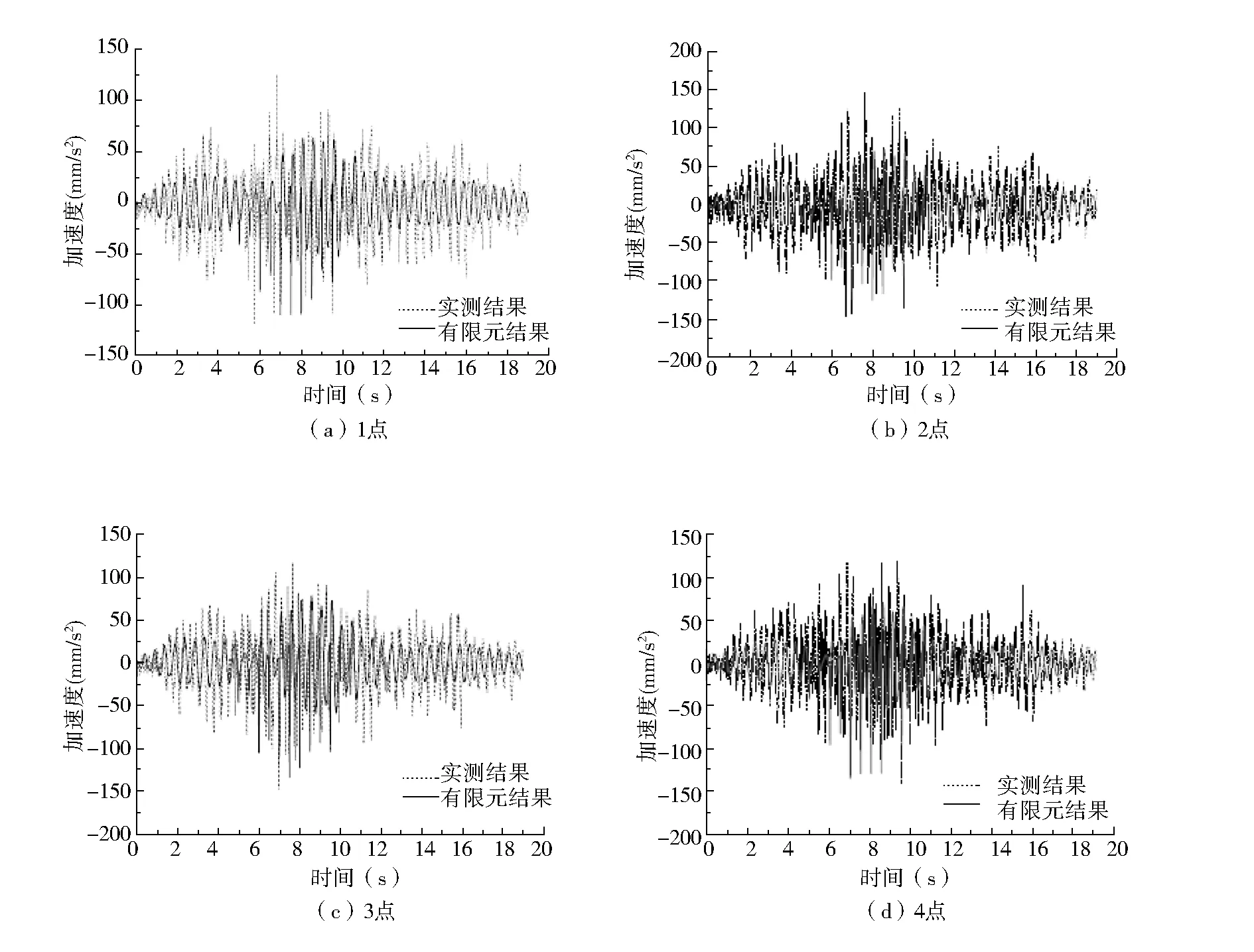
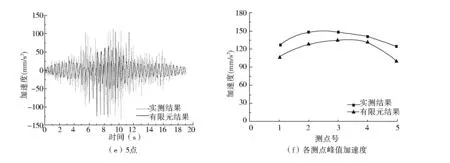
图9 工况八各测点加速度时程曲线及峰值曲线

3.4 定点激励类

定点激励采用在固定点加载法进行计算。定点激励也是国内外学者进行舒适度评价的加载方式之一。激励点的选择一般选在一阶振型振幅最大处,定点激励方式为连续行走或跳跃激励,计算完成后提取五个测点的竖向加速度时程曲线与实测结果进行比较。本小节仅仅是分析工况十和工况十二两种工况。

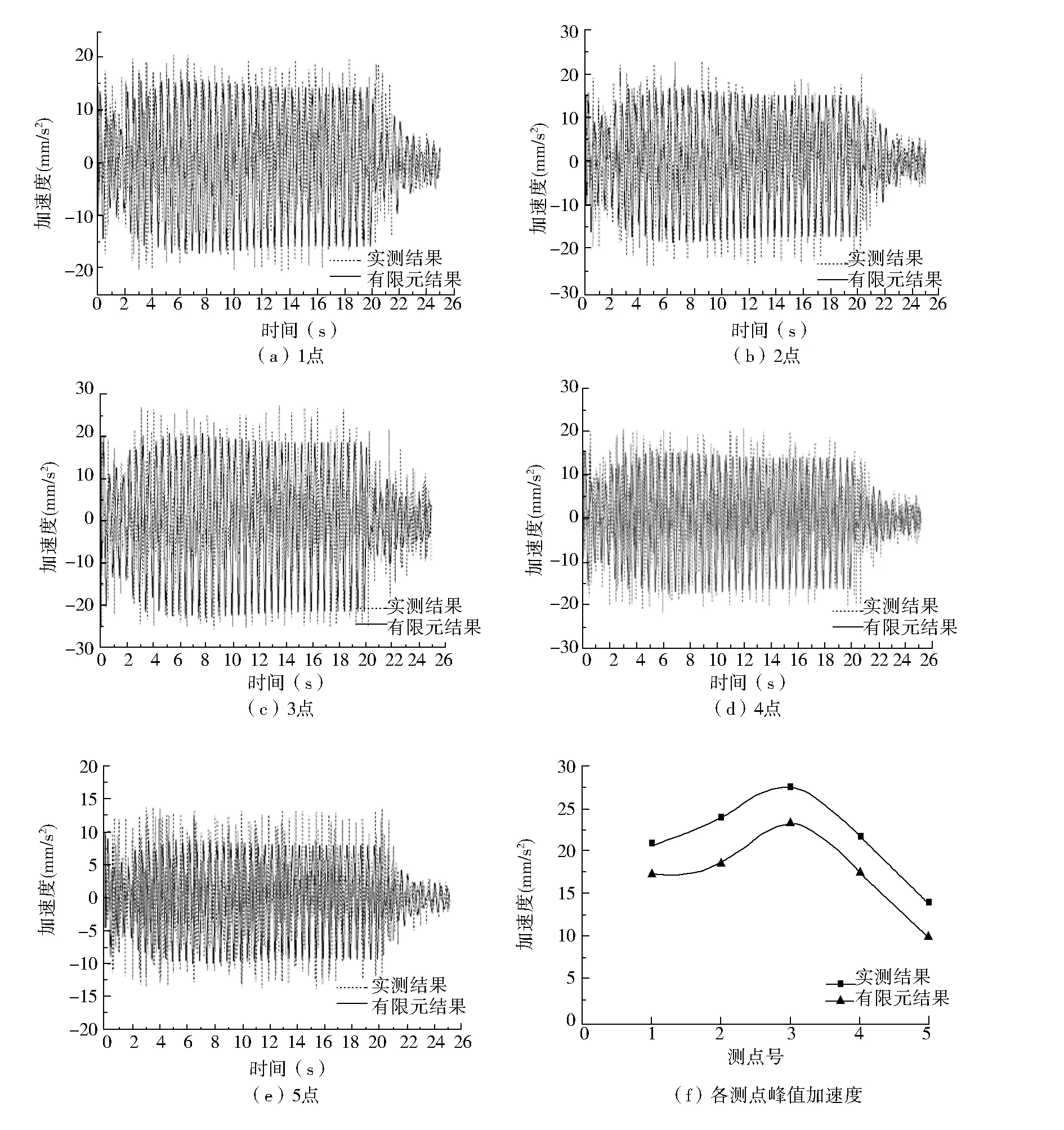
图10 工况十各测点加速度时程曲线及峰值曲线

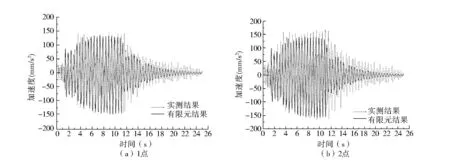
图11 工况十二各测点加速度时程曲线及峰值曲线

图10和图11分别为第十、十二工况下各测点加速度时程曲线及峰值曲线,分别对应在测点3处单人原地踏步20 s、在测点3处单人跳跃10 s、在测点3处五人跳跃10 s等定点激励工况。各测点加速度时程曲线较为平稳、饱满,停止激励后加速度衰减较快,实测时程曲线与有限元分析得到的时程曲线吻合较好,单人原地踏步产生的各测点加速度最小,最大仅为28.62 mm/s2,五人同时跳跃产生的加速度最大,其峰值加速度为181.722 mm/s2,接近于《高规》(203 mm/s2)规定的限值,因此应尽量避免在楼盖上出现多人同时跳跃等工况。

4 结论

本文通过一实际工程对第二跨楼盖进行了环境激励法模态试验,并与有限元结果进行比较,得出以下结论:

1)该种楼盖的低阶振型主要以竖向振动为主,类似于相同支承条件下的实心平板。

2)对装配式楼盖在十二种工况下竖向加速度响应进行了试验和有限元分析,试验结果和有限元结果吻合较好,所有工况均小于美国ATC指南及《高层建筑混凝土结构技术规程》(JGJ3-2010)规定的限值。

3)加速度最大点出现在行走路线1/2处,跑动路线上各测点加速度峰值明显大于偏离行走路线各测点加速度峰值,沿跨度方向各测点加速度衰减较快,沿纵向衰减较慢。

4)五人跑动和五人跳跃定点激励产生的加速度响应明显大于其他工况产生的加速响应,因此应尽量避免多人跑动及多人同时跳跃等工况的发生。