Probabilistic Automatic Outlier Detection for Surface Air Quality Measurements from the China National Environmental Monitoring Network
2018-10-16HuangjianWUXiaoTANGZifaWANGLinWUMiaomiaoLULianfangWEIandJiangZHU
Huangjian WU,Xiao TANG,Zifa WANG,Lin WU,Miaomiao LU,Lianfang WEI,and Jiang ZHU
1State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry,Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China
2International Center for Climate and Environment Sciences,Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China
3University of Chinese Academy of Science,Beijing 100049,China
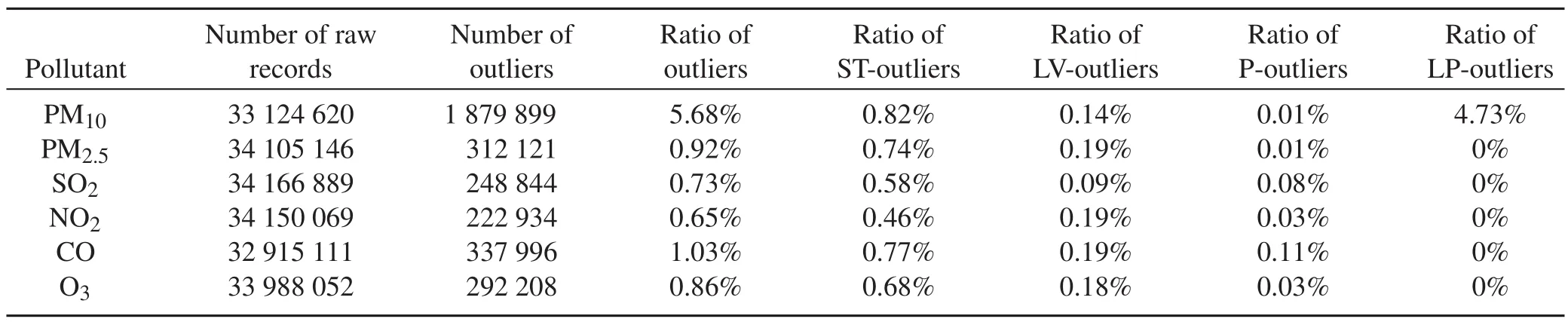
ABSTRACT Although quality assurance and quality control procedures are routinely applied in most air quality networks,outliers can still occur due to instrument malfunctions,the influence of harsh environments and the limitation of measuring methods.Such outliers pose challenges for data-powered applications such as data assimilation, statistical analysis of pollution characteristics and ensemble forecasting.Here,a fully automatic outlier detection method was developed based on the probability of residuals,which are the discrepancies between the observed and the estimated concentration values.The estimation can be conducted using filtering—or regressions when appropriate—to discriminate four types of outliers characterized by temporal and spatial inconsistency,instrument-induced low variances,periodic calibration exceptions,and less PM10than PM2.5in concentration observations,respectively.This probabilistic method was applied to detect all four types of outliers in hourly surface measurements of six pollutants(PM2.5,PM10,SO2,NO2,CO and O3)from 1436 stations of the China National Environmental Monitoring Network during 2014–16.Among the measurements,0.65%–5.68%are marked as outliers,with PM10and CO more prone to outliers.Our method successfully identifies a trend of decreasing outliers from 2014 to 2016,which corresponds to known improvements in the quality assurance and quality control procedures of the China National Environmental Monitoring Network.The outliers can have a significant impact on the annual mean concentrations of PM2.5,with differences exceeding 10 µg m−3at 66 sites.
Key words:probabilistic automatic outlier detection,air quality observation,low pass filter,spatial regression,bivariate normal distribution
1.Introduction
Surface pollutant measurements are fundamental in air quality as they provide crucial information for validating theoretical concepts,testing numerical models,and enabling applications such as data assimilation and ensemble forecasting.However,outliers can occur despite the quality assurance and quality control procedures applied by most air quality networks,consequently posing a considerable challenge for the various uses of surface pollutant measurements.Manual inspection(Fiebrich et al.,2010)is an effective choice to identify these outliers.However,this becomes cumbersome when facing large amounts of data,which makes it inapplicable to near real-time applications.Another limitation lies in the fact that data quality after manual inspection varies from operator to operator.Here,a probabilistic automatic method is proposed to detect outliers from China National Environmental Monitoring Center(CNEMC)surface pollutant measurements.
The CNEMC started to monitor the concentrations of six air pollutants(PM2.5,PM10,SO2,NO2,CO and O3)from 2012.By March 2017,the China National Environmental Monitoring Network(CNEMN)had included 1436 monitoring sites from 369 cities.Real-time hourly observations of the six pollutants at every monitoring site are uploaded to the CNEMC and released to the public(http://www.cnemc.cn/).These real-time observations are being assimilated into the chemical transport model at the CNEMC to improve air quality forecasts.They are also an important data source for the Ministry of Environmental Protection of the People’s Republic of China to assess urban air quality and establish air quality control strategies.The observations are widely used in many research fields,such as data assimilation(Tang et al.,2016),model verification(Wang et al.,2016),health impact(Li et al.,2017),satellite product verification(Gu et al.,2017),and analyzing the formation processes of pollution episodes(Shan et al.,2009;Zheng et al.,2015).
The quality of ambient air quality datasets is vital for interpreting results in related research fields.However,instrument malfunctions,the influence of harsh environments and the limitation of measuring methods can cause outliers in the observed datasets.For example,wearing,insufficient air tightness and excess axial resistance of the pump of the monitoring instrument will interfere with the measured values(Luo,2016).A blockage of the filter core or a breakage or running out of filter tapes can lead to significant errors in the monitoring of particulate matter.After rainstorms,observed concentrations of particulate matter might be negative if the mass of particulate matter accumulated is less than the water evaporated.Malfunction of the cooling system or the photomultiplier tube will cause NO2outliers,while instable infrared sources will cause CO outliers(Guan,2016).
Outlier detection involves separating inconsistent observations from regular ones,based on statistical or physical criteria that characterize the regular or inconsistent observations(Aggarwal,2016).Outlier detection has been widely applied to a diverse range of environmental data.In meteorology,outliers can be detected for those observations that are inconsistent in space and time(You et al.,2008;Steinacker et al.,2011;Liao et al.,2014),or against the characteristics of observed variables such as surface wind,precipitation and snowfall(Golz et al.,2005;Durre et al.,2010;Jiménez et al.,2010).There are also some detailed studies about outlier detection for variables in oceanography(e.g.,temperature and salinity profiles)and soil science(e.g.,temperature and moisture)(Ingleby and Huddleston,2007;Fiebrich et al.,2010;Dorigo et al.,2013).
Outliers in air quality are difficult to detect,because pollutants show particularly rich patterns of variations in space and time on multiple scales.These variations are driven by complex processes of chemical reactions,atmospheric transport,emissions and depositions,and thus cannot be easily represented by either statistical models or chemistry transport models.Recent outlier detection studies in air quality mainly probe the inconsistency in space and time in pollutant concentration observations from clusters of stations.For instance,Kracht et al.(2014)identified outliers as daily PM10measurements that manifest extreme values compared with the smoothed values—the weighted averages from neighboring background stations in the European air quality database AirBase;whereas,Bobbia et al.(2015)compared hourly PM10measurements with the weighted median from nearestneighbor stations or with geostatistical spatial predictions using classical kriging techniques.Araki et al.(2017)performed leave-one-out predictions of daily mean PM2.5and NO2in Japan using ordinary kriging of residuals from a land use regression model,and identified observations with large kriging errors as outliers.Interestingly,Čampulová et al.(2015)proposed an automatic procedure to mark out potential outliers from two urban stations measuring hourly PM10concentrations by checking whether observations lie in a plausible interval obtained by analyzing residuals of data smoothing.
The main challenge for outlier detection in air quality is that the true spatiotemporal variations of pollutants can only be estimated to serve as detection criteria to separate outliers from signals,while all estimations have limitations.For instance,in kriging estimation,a more detailed diurnal covariance structure can be introduced(Wu et al.,2010),but covariance modelling in high dimensional space is a very difficult issue(Bickel and Levina,2008).In practice,manual inspection(Fiebrich et al.,2010)is still an effective choice to identify outliers.A majority(80%)of outliers were identified by manual inspection at four sites in Shanghai in China from 2014 to 2016(Guan,2016).In this paper,outliers are classified into four types based on their characteristics.Then,an automatic outlier detection framework is proposed based on the probability of residuals between the observations and their estimation discriminating the known characteristics of different types of outliers.Our hope is that this probabilistic outlier detection method will help in routinely identifying outliers in pollutant observations from the CNMEC in an automatic manner such that cumbersome real-time manual inspections can be avoided.Subsequently,better datasets could be constructed to support various research aims related to the severe air pollution problem that is currently a national concern in China.
2.Methods
2.1. Outlier classification
Complex sources of errors in observational datasets make it difficult to identify the cause of errors based on the observed data itself(Sciuto et al.,2013).Therefore,outliers are classified into four types based on their characteristics:
(1)Spatially and temporally inconsistent outliers(ST-outliers).Similar to meteorological parameters(Steinacker et al.,2011),the scale of pollution phenomena exceeds that resolved by the observational network,and one can expect the measured concentrations to be smooth both in time and space.Observations that differ greatly from values observed at the adjacent time or in neighboring areas are defined as ST-outliers.
(2)Low variance outliers(LV-outliers).This type of outlier has a very low variance in time series compared to neighboring sites.Some LV-outliers do not change over time and can be observed when the pump of the instruments is stuck or the filter tape is depleted.Most outliers that change very slowly come from CO observations measured by the pressure difference between two chambers.These outliers can be observed when the aging of the light sources in the two chambers is not synchronized(Luo,2016).
(3)Periodic outliers(P-outliers).This type of outlier usually appears every 24 h,as shown in Fig.1e.For some in-struments,the accuracy may decrease with time due to the ageing of light sources and the changing of the ambient environment.Regular calibration is required for such instruments.However,the calibration processes may interfere with the observations,thus inserting abnormal values into the online measurement datasets.
(4)Lower PM10than PM2.5outliers(LP-outliers).This type of out lier involves PM2.5concentrations being higher than PM10concentrations observed at the same hour and same site.Most PM2.5monitors in the CNEMN network were installed around a decade after the PM10monitors,with more advanced instruments used for PM2.5monitoring,and the loss of semi-volatile components of particulate matter is better handled(see section 2.7 for details).Therefore,PM2.5data are more reliable than PM10data,and PM10data are marked as LP-outliers if the observed concentration of PM2.5is higher than that of PM10.
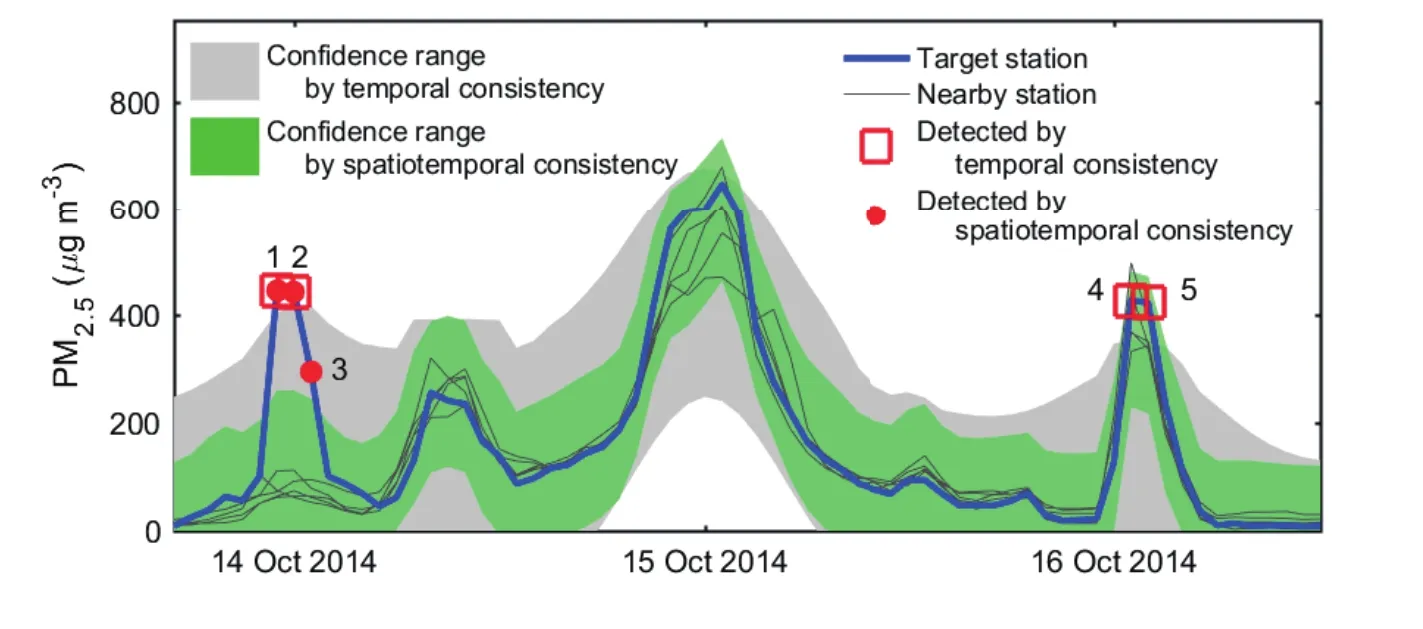
Figure 1 shows examples of classified outliers.It is importantto note that the four types of outliers are not exclusive.Some P-outliers are also ST-outliers,and some LP-outliers are also LV-outliers.
2.2.Probabilistic automatic outlier detection
The most common technique for identifying outliers in meteorological data is thez-score method(Lanzante,1996;Feng et al.,2004;Durre et al.,2010).This method normalizes the observed values using their mean and standard deviation,then removes those values whosez-score exceeds a specified threshold.Thez-score is calculated as follows:
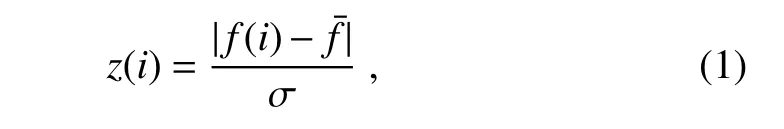
wheref(i)andz(i)are the observed value andz-score at timei;¯fand σ are the mean and standard deviation of the observed values.
Thez-score method can identify outliers that are considerably deviated from most observations. The limitation of this method is the normal distribution assumption made for observations(Durre et al.,2010),when in fact pollutant concentrations are always positive and their distributions are known to be closer to lognormal(Leiva et al.,2008).To deal with this limitation and combine detection methods by probability theory,three modifications are made to thez-score method:
(1)Instead of directly assessing the pollutant concentration observations,the residuals between the observed and the estimated concentration values are evaluated:

Here,F(i)is the estimated concentration at timei.Such an estimation can be conducted using either filters or regression models.Observations with large residuals are more prone to be marked as outlier candidates.

Fig.1.Samples of outliers.(a,b)Spatiotemporal outliers have large differences with neighboring observations in time and space.(c,d)Low variance outliers either stay the same or change abnormally slowly in time and differ significantly with observations from nearby sites.(e)Periodic outliers appear periodically,usually every 24 h.(f)PM10 (2)The standard deviation of the residuals is computed within a sliding window and updated constantly so that the outlier detection method will be more sensitive to local outliers.The standard deviationSof the residuals is calculated by wherei−nandi+nare the start and end of the sliding window. Substituting the observed valuesfand the standard deviation σ in Eq.(1)by the residualRand its standard deviationsS,it becomes: Generally,the mean of residuals¯Rshould be zero,and the calculation of probability is not affected by the sign ofZ.The numerator|R(i)−¯R|can then be simplified toR(i);therefore, (3)Instead of thez-score values,the probability ofZis introduced as a criterion to determine whether or not an observation is abnormal.Thez-values in Eq.(5)are set to be normally distributed,and its probability is calculated by The normal distribution is chosen because it is a central distribution appropriate for residuals;plus,among all distributions with a given mean and a given variance,the normal distribution maximizes the entropy and is thus least informative.The introduction of the probability provides a framework based on which multiple rules for identifying abnormal observations can be combined(see sections 2.4.3 and 2.5).Next,we provide further details on how to use this probabilistic automatic outlier detection(PAOD)method to identify different types of outliers in surface observations of air pollutants. The first detection involves identifying and removing outliers with large observational errors.These outliers might increase the residuals of normal observations and decrease the residuals of outliers.They make it more difficult to identify outliers with small observational errors,and should be removed before other detections.The detection and removal of outliers with large errors consists of the following two steps: (1)Firstly,outliers exceeding the measurable range of the instrument are removed.The measurable range of the instrument for the six pollutants are specified by China National Standards(HJ653-2013,HJ654-2013),as listed in Table 1. (2)In the second step,the PAOD method described in section 2.2 is applied to further identify outliers with largeobservational errors.Here,the estimated values are calculated by a median filter[Eq.(7)],which is less likely to be affected by the outliers: Table 1.Measurement ranges of the monitors used in the CNEMC’s air quality monitoring network. whereFmis the value estimated by the median filter at timei;M is the median function;i−nandi+nrepresent the start and end of the sliding window.The length of the sliding window,2n+1,is set to one month. The residualRmis obtained by substitutingFminto Eq.(2).The standard deviation of the residualSmis calculated using the median absolute deviation(MAD),as follows: Compared with the conventional method described by Eq.(3),obtaining the standard deviation by MAD is more robust to outliers(Dunn et al.,2012).The probabilityPmcan be calculated through using the regression residualRm,its standard deviationSmand Eqs.(5)and(6).The probability threshold is set to 10−15after several sensitivity tests,and the data with probabilityPmless than the threshold value are marked as outliers and removed from the datasets. After removing the outliers with large observational errors,spatiotemporal outlier detection is implemented to remove the ST-outliers described in section 2.1.To better identify these outliers,both the observed data of the target site at adjacent times and the data at neighboring sites are simultaneously used.The spatial and temporal residuals are assumed to follow the bivariate normal distribution,which makes it convenient to combine the estimations from both temporal and spatial estimation models. 2.4.1.Temporal consistency estimation The estimation of pollutant series of temporal consistency is carried out using a low-pass filter: Table 2.Filter coefficients and the time shift for the low-pass filter used in the temporal consistency estimation. whereFt(i)is the estimated value at timei,fis the observed value at the target site,andh(k)represents the low-pass filter coefficient(listed in Table 2).The filter coefficients are calculated following the algorithm designed by Karam and McClellan(1995),and the passband and stopband frequency is set to 1/8 and 1/24 h,respectively.The low-pass filter tends to preserve the low-frequency signals of normal variations from atmospheric chemistry and restrain the abnormal high frequency signals accompanied by outliers.Compared with a moving average,it makes the residuals of normal observations smaller through giving higher weights to the data closer to the checkpoint. 2.4.2.Spatial consistency estimation The pollutant series of spatial consistency is estimated by spatial regression: whereFs(i)is the estimated value at the checkpointi;fris the observed value from neighboring siter;arandcrare the index of agreement and localization coefficient between the target and a neighboring site. Following the method of Legates and McCabe(1999),the index of agreement is defined as wherefris the observed value at neighboring sites,andis the time-average offrwithin the sliding window.The length of the sliding window,2n+1,is also set to one month. The index of agreement is often employed to evaluate the simulated results of models,and has been used in quality assurance as well(Durre et al.,2010).It provides a measure for both the covariation and the absolute difference between the data of two time-series.Compared with the correlation coefficient,it is less affected by outliers,but still affected by sampling errors.To deal with this problem,this paper borrows the idea of localization from data assimilation and adopts a localization method introduced by Gaspari and Cohn(1999).The method reduces the influence from remote sites,and the localization coefficient is calculated as follows: wheredis the distance between the target and a neighboring site,anddcis the characteristic length of localization. 2.4.3.Combining temporal and spatial consistency estimations After obtaining the estimated valuesFtin Eq.(9)andFsin Eq.(10)using the observed data at adjacent times and the data at neighboring sites respectively,the corresponding residuals at the checkpoints can be calculated using Eq.(2).Then,the residuals are normalized toZtandZsusing Eqs.(3)and(5).The spatial and temporal consistency are evaluated simultaneously under our PAOD framework, and compute the probability ofZtandZsby a bivariate normal distribution: wherePst(i)is the joint probability at timei,and ρ is the correlation coefficient betweenZtandZs: Here,ZtandZsare the means ofZtandZs,respectively,within the sliding window;i−nandi+nare the start and end of the sliding window.Observations with low probability at the checkpoint are identified as outliers. Figure 2 displays the outliers detected in two ways.One uses the joint probability ofZtandZs,and the other only employs the probability ofZt(only considering the temporal consistency).When only the temporal consistency is considered,the method identifies the outliers at checkpoint Nos.1 and 2,but misses the outlier at No.3 and misrecognizes the normal observations at Nos.4 and 5 as outliers.After using the joint probability,the method deals with the above defects properly.This suggests that the detection method using the joint probability of the residuals improves the accuracy of the detection method.The two detection methods are applied to the raw data described in section 3.For PM2.5,PM10,SO2,NO2,CO and O3observations,37%–83%of the data marked with spatiotemporal inconsistency are also marked with temporal inconsistency.For some outliers with moderate temporal inconsistency but strong spatial inconsistency(such as observation 3 in Fig.2),it can only be identified by the detection using spatiotemporal consistency.Among the data marked with spatiotemporal inconsistency,46%of them are not marked by the detection using temporal inconsistency.For normal observations with strong spatial consistency but week temporal consistency(such as observations 1 and 2 in Fig.2),it might be misidentified by the detection using temporal inconsistency.Among the data marked with temporal inconsistency,54%of the them are not marked by the detection using spatiotemporal consistency. To deal with the LV-outliers that stay the same or change slowly,the low variance periods are first detected by checking the first and second derivatives of the observed values over time.As some low variance observations will be normal observations when the ambient air is clean or stable,the spatial consistency is combined to decide whether the data in those periods should be mark as outliers.The residual of a low variance period is an average of the residuals of the spatial consistency estimation in this period: whereRs(i)is the residual of the spatial consistency estimation,as in section 2.4.2,andbandeare the beginning and end of this period.The standard deviation ofRvis calculated according to the standard error of the mean for samples that are normally distributed: whereSs(i)is the standard deviation of the residuals of the spatial consistency estimation in section 2.4.2.Using Eqs.(5)and(6),the normalized residualZvand its probabilityPvfor the whole period can be obtained.IfPvis smaller than a predefined value(10−6in this study),the data within the whole period are identified as LV-outliers. P-outliers are mainly caused by the daily self-calibration of the instrument and appear every 24 h.According to this characteristic,the time series of the observed data within 11 days are firstly processed into diurnal-variation data: wherefis the hourly observed concentrations andfpis the data after processing.Then,a median filter is applied: whereFp(i)is the estimated value and M is the median function. Instead of Eq.(3),the standard deviationSp(i)of the residuals is calculated using the following method: Fig.2.Comparison of outlier detections based on temporal consistency and spatiotemporal consistency. The detection based on spatiotemporal consistency can detect outliers 1,2 and 3 while preserving valid observations 4 and 5. whereRpis the residual andgis a function that finds the 93.75th percentiles.The advantage of using the 93.75th percentiles of the residuals is that the obtained standard deviation is the second largest residual in one day,and only the observation with the largest residual in a day might be identified as the P-outliers.Using Eqs.(5)and(6),the probabilityPpof the residual can be obtained.IfPpis smaller than a predefined value(10−4in our check),the corresponding observation will be identified as the P-outliers.Figure 3 gives an example of the P-outliers that shows a peak concentration of ozone at 0400 LST(LST=UTC+8)every day.It should be noted that most of the P-outliers present large differences from their neighboring observations and can be identified by the detection of ST-outliers in section 2.4.However,there are also some P-outliers that have a relatively small difference from the neighboring observations and need to be identified by the P-outlier detection. The last detection is to mark the outliers with an observed concentration of PM2.5higher than that of PM10at the same hour and same site.This step is very simple but very important for the observed datasets from the China Nationwide Air Quality Monitoring Network.The PM2.5and PM10are mainly measured by the beta attenuation monitoring method(BAM)or tapered element oscillating microbalance method(TEOM).Both methods use heaters to reduce the humidity of the sampled air to prevent fogging and inhibit particle growth under high humidity.However,the heating process may lead to the volatilization of semi-volatile organic compounds of particulate matter.To deal with this problem,most new monitors adopt a filter dynamic measurement system to measure the volatile portion of the sample air when the concentrations are measured by TEOM.Also,a smart heater is implemented when the concentrations are measured by BAM,to keep the relative humidity at around 35%instead of keeping the temperature at around 50°C.The PM2.5monitoring started from 2013,about a decade later than the PM10monitoring.A filter dynamic measurement system or a smart heater is mandatory for the PM2.5measuring instruments,while they are optional for the PM10measuring instruments.Also,neither of them is implemented for most PM10measuring instruments that were established before 2013(Pan et al.,2014).As a result,the PM2.5data are more reliable than the PM10data,and the LP-outliers are more likely to occur at nighttime and on foggy days when the relative humidity is higher(Niu,2017). Most outliers or“bad data”in the observed PM10data are LP-outliers before 2016.The percentage of“bad data”can be higher than 7%(Fig.4).However,as measuring instruments and management have been upgraded,the percentage of“bad data”had reduced to about 1%in 2016,and will hopefully continue to decrease in the future. The PAOD method was applied to detect outliers in the raw data of the hourly observations of six pollutants(PM2.5,PM10,SO2,NO2,CO and O3)during 2014–16.The raw data were monitored by the CNEMN network.The network contains 1436 monitoring stations across China,and the monitored data are directly transmitted to the data center at the CNEMC.The raw data in this paper are hourly observations directly acquired from the data center at the CNEMC.The number of outliers identified by the method and their proportions are shown in Table 3.Among the raw data,0.65%–5.68%are identified as outliers. There are more outliers in the PM10and CO observations than other pollutants,accounting for 5.68%and 1.03%respectively.The NO2and SO2observations have fewer outliers than the other pollutants,accounting for only 0.65%and 0.73%respectively.For PM2.5,SO2,NO2,CO and O3observations,the ST-outliers are the most frequent among the four types of outliers,accounting for 0.46%–0.77%of the raw data.The LV-outliers rank second,accounting for 0.09%–0.19%.The P-outliers are an important type of outlier for gaseous pollutants,especially CO and SO2.For PM10observations,the LP-outliers account for 4.73%of the raw data and are the main source of abnormal observations(see section 2.7 for why the PM2.5data are more reliable than the PM10data). Fig.3.Periodic outliers of O3observations detected for a site in Wuhan,China,between 22 and 30 August 2014.Some periodic outliers can be detected by spatiotemporal consistency,while others have relatively small measurement error compared to the variation of neighboring observations and can only be identified in the detection of periodic outliers. Table 3.Number of hourly observations in China from 2014 to 2016,as well as number and ratio of outliers detected. Fig.4.Outlier ratio of all sites in China From 2014 to 2016.Outlier ratios decrease more or less for all the six pollutants from 2014 to 2016.Most of the reduction in the ratio of PM10outliers comes from the decrease in PM10 Figure 4 shows the removal ratios of the six pollutants during the three years.The removal ratio is the fraction of raw data being labeled as outliers.During 2014–15,the PM10observations have a high removal ratio(more than 7%).Most of the removed data are LP-outliers.However,in 2016,the removed ratio decreases sharply to about 1%.This might be related to the implementation of a compensation algorithm for the loss of semi-volatile materials in the PM10measurements.Interestingly,the removal ratios of the PM2.5,SO2,NO2,CO and O3observations also decrease.This indicates that the data quality of the CNEMN has been improved from 2014 to 2016. To evaluate the impact of the outlier detections on the observed concentrations,Fig.5a compares the observed annual PM2.5concentrations before and after quality assurance in Shijiazhuang City during 2014–16.The results show a big difference of more than 150 µg m−3for estimating the annual mean concentration in 2014,which is mainly caused by some outliers that exceed the measurement range.Figure 5b presents the diurnal variations of the observed O3concentrations before and after quality assurance at a site in Wuhan in 2015.Due to the P-outliers that occurred at 0400 LST,the raw data display a false peak at that time.The quality assurance reduces this false peak,and the data after quality assurance show more reasonable daily variations of O3concentrations. Figure 6 displays the differences in annual concentrations caused by outliers in 2015.For PM2.5,the differences are lower than 1µg m−3at most sites.However,there are 66 sites and 17 sites whose differences are greater than10µg m−3and 50 µg m−3respectively.For PM10,the differences at most sites are within 1–10 µg m−3,while there are 92 sites and 23 sites with differences greater than 10 µg m−3and 50 µg m−3respectively.For CO,big differences of more than 1 mg m−3can be observed at 80 sites.For O3and NO2,the differences are relatively small,and only a few stations(<20)have differences of more than 10µg m−3.For SO2,there are 38 sites with differences of more than 10 µg m−3.The above results suggest that outliers might lead to significant biases in the estimation of annual mean concentrations of these six pollutants.Identifying and removing outliers is a necessary step before using the online dataset. A POAD method is proposed to detect outliers for hourly surface concentration observations of six pollutants(PM2.5,PM10,SO2,NO2,CO and O3)from the 1436 stations of the CNEMN during 2014–16.This outlier detection method takes advantage of the known characteristics of outliers[temporal and spatial inconsistency(ST-outliers),instrument induced low variances(LV-outliers),periodic calibration exceptions(P-outliers),and less PM10than PM2.5in concentration observations(LP-outliers)]by computing the probability of residuals between the observations and the estimations that discriminate these known characteristics of outliers.The outlier detection process is fully automatic;hence,it will help in avoiding the cumbersome manual inspection of outliers when seeking to achieve reliable air quality data in the CNEMN network. Fig.5.(a)Annual PM2.5concentration in Shijiazhuang city before and after quality assurance.(b)Diurnal cycle of O3before and after quality assurance for a site in Wuhan,China,2015. The outliers detected account for 0.65%to 5.68%of the observations for the six pollutants.PM10observations have the most outliers,among which LP-outliers contribute the most(see section 2.7 for why the PM2.5data are more reliable than the PM10data).The proportions of outliers in the six pollutants all decrease from 2014 to 2016,which suggests an improvement in the data quality of the CNEMN network.The impact of outliers is estimated by the difference in annual mean concentrations of PM2.5between the raw data and the data after outlier detection.The differences are less than 1µg m−3at most sites,but there are 66 sites whose differences are greater than 10µg m−3.This suggests that outlier detection is essential before using the monitoring datasets,even for evaluation of the annual mean concentrations. The outlier detection method was developed with the help of the CNEMC,which is also the institute responsible for releasing the real-time air quality data.The method has been used in the assimilation system of the CNEMC,and is going to be integrated into the data management system.Hopefully,outliers in the real-time air quality data will be removed by our method in the near future. Although the application of the PAOD method has brought some positive and interesting results,improvements can still be made for better performance in further in-depth studies.First,the outlier detection method is performed separately for each species;however,these different pollutants are closely linked to one another by atmospheric chemistry.Further developments of the outlier detection method could take into consideration information from multiple pollutants at the same time to account for chemical transformations.Second,the method does not take into account the specific locations of the stations in the urban environment.Stations in the proximity of heavy traffic highways will have much stronger variations in observations than those in urban green spaces.Developing different parameters sets for different types of stations might improve the performance.Third,the outlier detection method assumes that outliers account for a small proportion of the raw data.However,at some stations,most of the raw data on a weekly basis can be bad data,providing little or no information on reals concentrations.Examination of the distributions within the raw data might help in such cases.Finally,this method uses the normal distribution to compute the probability of residuals.However,when more information is available,new distribution types should be tested to better adapt to the CNEMN dataset. Acknowledgements. The authors express their sincere gratitude to the CNEMC for providing the air quality observations for the period 2014–16.This study was supported by the National Natural Science Foundation(Grant Nos.91644216 and 41575128),the CAS Information Technology Program(Grant No.XXH13506-302)and Guangdong Provincial Science and Technology Development Special Fund(No.2017B020216007).


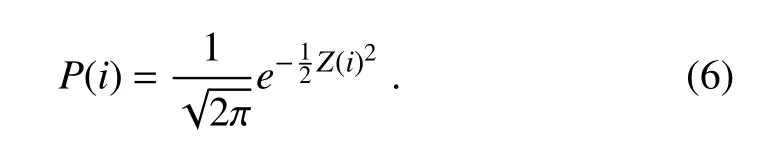
2.3.Detection of outliers with large errors

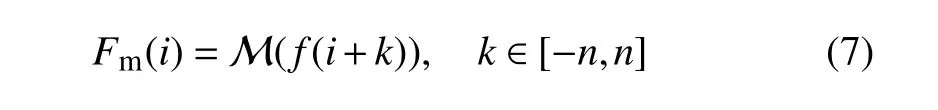

2.4.Detection of ST-outliers
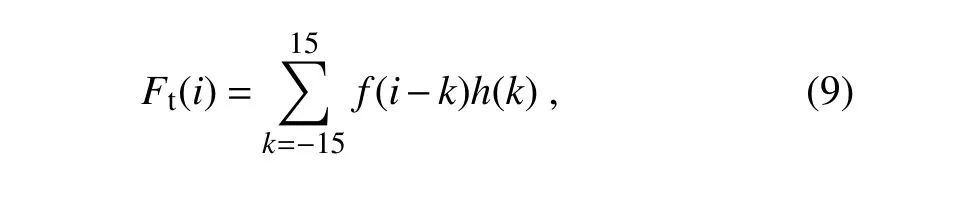




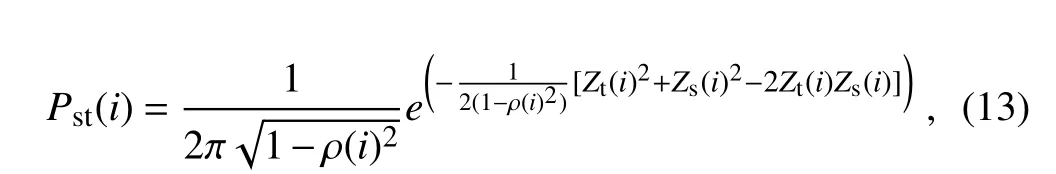
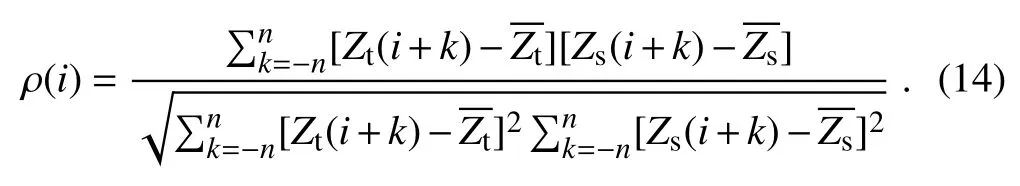
2.5.Detection of LV-outliers


2.6. Detection of P-outliers
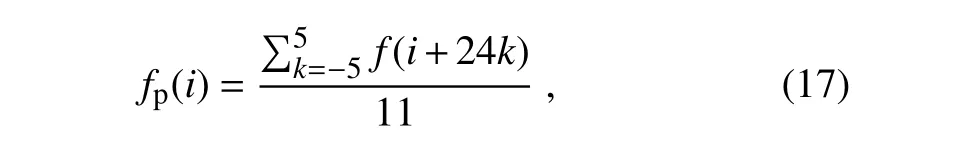

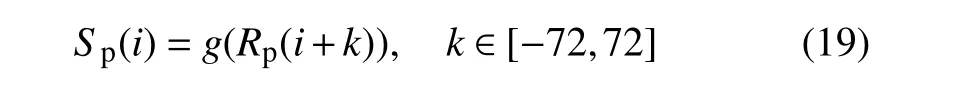
2.7.Detection of LP-outliers
3.Results


4.Conclusions and future work

杂志排行
Advances in Atmospheric Sciences的其它文章
- A 31-year Global Diurnal Sea Surface Temperature Dataset Created by an Ocean Mixed-Layer Model
- Nocturnal Low-level Winds and Their Impacts on Particulate Matter over the Beijing Area
- Impact of Interannual Variation of Synoptic Disturbances on the Tracks and Landfalls of Tropical Cyclones over the Western North Pacific
- Two Types of Flash Drought and Their Connections with Seasonal Drought
- Electronic Supplementary Material to:Two Types of Flash Drought and Their Connections with Seasonal Drought∗
- Estimating the Predictability Limit of Tropical Cyclone Tracks over the Western North Pacific Using Observational Data
