基于层次聚类和极限学习机的母线短期负荷预测

颜宏文，盛成功

(长沙理工大学 计算机与通信工程学院，长沙 410114)(*通信作者电子邮箱yan_hongwen@126.com)

0 引言

母线负荷可以定义为由变电站的主变压器供给一个相对较小的供电区域的终端负荷的总和[1]，是系统负荷的细化。对母线负荷的精确预测是改善电网安全性、稳定性和经济性，提高用电质量的重要保证。母线负荷不同于系统负荷，它具有以下特点：母线负荷易受气象因素变化影响，如气温的突然升高和降低，将引起居民用电特别是空调负荷的剧烈变化，大面积降雨后会引起排渍负荷的突然增加[2]；电网系统中母线数目众多、量大面广、负荷基数小，波动性大，不同母线之间负荷差异较大，难以人工逐一深入分析。因此，对母线负荷进行精准的预测具有较高的难度。

国内外众多学者对母线负荷预测进行了大量研究。文献[3]采用的是模糊系统和人工神经网络的方法；文献[4]提出了辅助预测状态估计和多层感知器神经网络组成的混合预测方法；文献[5]引入预测模型有效度概念，提出基于关联度的组合模型集确定方法和模型有效度灰色预测方法；文献[6]针对正常日的母线负荷，提出基于最小二乘支持向量机和马尔可夫链的预测方法；文献[7]提出小波分解的支持向量机预测母线负荷的方法；文献[8]根据母线负荷源荷属性进行分类，将地区有源网的电源成分和负荷成分分开考虑，改进母线负荷的预测方法等。但以上方法笼统地用待测日之前一段时间作为相似日，没有考虑到影响母线负荷波动的因素而造成的特殊性,如季节、气候、星期及节假日规律等多重因素对负荷变化的影响一直制约着预测精度的提高[9]。对于节假特殊日来说，例如，春节假期与春节假期之前虽然日期相邻，但是负荷一般会相差非常大；同理，对于天气特殊日来说，在季节交替之时，天气会出现骤变的情况，导致相邻日期的负荷相差较大。如果使用这些特殊日之前的母线负荷作为训练样本，特殊日的负荷预测会存在较大偏差。

本文提出一种基于层次聚类(Hierarchical Clustering， HC)和极限学习机(Extreme Learning Machine， ELM)的母线短期负荷预测方法。该方法先用层次聚类法对历史负荷进行聚类，结合历史日的气象信息和日期类型建立决策树，得到分类规则；然后将待测日属性根据分类规则查询到该日的负荷分类类型，用该类的历史母线负荷数据训练极限学习机并对待测日母线负荷进行预测。该方法充分考虑天气因素和日期类型对母线负荷的影响，不仅能提高对普通日的母线负荷预测精度，而且对特殊日期的负荷预测也有较好的效果。

1 基于HC和ELM的母线短期负荷预测模型

1.1 ELM

为了克服前馈神经网络学习速度较慢的缺点，Huang等[10]提出一种名为ELM的新型单隐含层式前馈神经网络。ELM基于经验风险最小化理论，其训练过程只需要一次迭代，与其他神经网络相比具有更加优越的泛化能力、鲁棒性和更快的学习速率。目前ELM被广泛用于分类、预测和回归问题，因此本文也采用ELM预测母线负荷。ELM的核心是随机设置输入权值和偏差，通过最小化训练误差来优化输出层的权值。

设有N个训练样本{(ξi,τi)|ξi∈Rn,τi∈R,i=1,2,…,N}，其中ξi=[ξi1,ξi2,…,ξin]为输入向量，τi是对应的期望输出值。含有M个隐层节点和激活函数为f(x)的ELM数学模型可以表示为：

(1)

其中：ωi=[ωi1,ωi2,…,ωin]T表示连接第i个隐层节点和输入节点权值；βi=[βi1,βi2,…,βin]T表示连接第i个隐层节点和输出节点的权值；εi=[εi1,εi2,…,εiM]T表示第i个隐层节点的偏差。式(1)可以用矩阵的形式简写：

Y=Tβ

(2)

其中：

T=

(3)

其中，T为隐层节点的输出矩阵。输出权值的求解是保证损失函数(4)取得最小值：

(4)

可由解以下方程组(5)的最小二乘解求得:

(5)

其中T+是矩阵T的Moore-Penrose广义逆矩阵[11]。

1.2 历史母线日负荷聚类

(6)

先将历史母线日负荷的96点数据作为一个原子簇，计算邻近度矩阵，簇之间的邻近度采用组平均规则计算，相继合并两个最接近的簇，直到只剩下一个簇[12]，或者满足某个最终条件。

如果聚类数目太小，差异较大的样本数据就会划分到同一类中，这样得到历史相似日的母线负荷特征相差较大，从而导致ELM预测模型预测不准确；然而如果聚类数目太大，个别类中的样本数据过少，本属于同一个聚类的样本数据就会划分到不同的聚类中，也会增大ELM预测模型的预测误差。因此，母线负荷预测的一个关键问题就是选择合适的聚类数目，针对不同的母线负荷特征，选择的聚类数目也会有所差异。

本文研究了湖南省某两类220 kV母线日负荷数据，为了预测的准确性，经作者实验选取的聚类数目为20，不仅能保证类中有足够的数据样本数，而且能保证高相似度的数据样本聚为一类。

1.3 决策树

决策树是功能强大的分类和预测算法，它是一种有监督的学习算法，以树状图为基础，其输出结果为一系列简单使用的规则[13]。决策树生成算法中，经典的ID3算法用信息增益选择属性，存在倾向于选择取值多的属性的不足[14]，在此基础上提出的改进算法C4.5则采用信息增益比率作为在增长树的每一步中选取最佳属性特征的度量标准[15]。在树构造过程中进行剪枝，不仅能够完成对连续属性的离散化处理，而且能够对不完整数据进行处理，产生的分类规则易于理解，准确率更高，故本文采用的决策树算法为C4.5算法。

母线日负荷以及其聚类结果都由每日的天气情况和日期类型直接决定，因此，可以用决策树将此关系以树状图的方式呈现出来，历史母线负荷的聚类结果和影响因素分别作为决策树的结果节点和决策值。针对影响母线负荷的因素，本文选取每日24点实际天气信息数据的日最高气温、日平均气温、日平均相对湿度作为衡量影响母线负荷的天气因素；星期类型分为星期一至星期日；节假日类型分为国家法定节假日、节假日的后一日和普通日。

1.4 母线负荷短期预测算法设计

传统的母线负荷预测模型更多使用待测日前一段时间的历史负荷数据训练预测模型，但天气、星期类型和节假类型的不同会导致前一段时间与待测日的特征相差很大，导致预测精度欠佳。为了充分考虑天气因素和日期类型对母线负荷的影响，提高对普通日的母线负荷预测精度，更好地预测特殊日期的母线负荷，本文采用层次聚类法先对历史母线负荷进行聚类，结合历史日的气象信息和日期类型建立决策树，得到分类规则，将待测日属性根据分类规则查询到该日的负荷分类类型，用该类的历史母线负荷数据训练极限学习机并对待测日母线负荷进行预测。

基于HC和ELM的母线负荷短期预测模型输入为220 kV母线96点的历史负荷数据、历史天气数据和日期类型以及待测日的天气数据和日期类型；输出为预测日96点的负荷值。

基于HC和ELM的母线负荷短期预测算法步骤为：

1)输入历史母线日负荷96点数据，采用层次聚类法对其进行聚类。

2)选取以下日属性作为决策树的决策值：

①天气因素：日最高气温、日平均气温和日平均相对湿度；

②日期类型：星期类型和节假日类型。

3)数据数量化和归一化。星期类型数量化为D={1,2,3,4,5,6,7},其中1至7依次代表星期一至星期日。将节假日类型数量化为H={0,1,2},其中0表示该日是国家法定假日，1表示该日为国家法定节假日之后的第一天，2表示其他日期。本文采用线性变换的方法进行数据归一化处理，公式如下：

yi=(xi-xmin)/(xmax-xmin)

(7)

其中:xi是样本数据需要转换的数值，yi是样本数据转换后的数值，xmax是该样本数据中的最大值，xmin是该样本数据的最小值。

4)历史母线日负荷经层次聚类得到的分类结果作为决策树的结果节点，并建立决策树。

5)经天气预报得到待预测日的日最高气温、日平均气温和日平均湿度，另外查询得到其星期类型和节假日类型的日属性，根据建立的决策树的内部节点自顶向下得到分类规则，在叶节点得到待预测日的分类。

6)极限学习机参数设置。本文极限学习机的输入层和输出层节点数设置为1，隐层节点数为80。

7)在聚类结果中得到该类历史母线负荷，用其训练极限学习机，输出最终预测值。

以上算法预测流程如图1所示。

图1 母线负荷预测流程

2 实验分析

本文实验硬件环境为Intel Core i5 2.53 GHz的CPU，内存为2 GB RAM，软件环境为Windows 7操作系统、Matlab R2010a和Python 3.4开发环境，所使用的程序语言为Matlab和Python。本文提出的基于HC和ELM的预测算法简记为HC-ELM。母线历史负荷、日最高气温、日平均气温、日平均湿度、星期类型以及节假日类型使用预测日前一年内的历史数据。以平均绝对百分比误差(Mean Absolute Percentage Error，MAPE)作为误差评价标准，其计算公式为：

(8)

实验对象采用湖南省某两类不同的220 kV母线的历史数据，两条母线分别称之为母线1和母线2。对母线1的2016年2月7日进行母线负荷预测，该日为春节的第一天；对母线2的2015年12月24日进行母线负荷预测，该日为普通日。分别对以上两个预测日前一年365日的历史负荷数据进行层次聚类，两条母线的聚类结果分别如表1、2所示。

由表1和表2可知，母线1、2均各自有365个样本数据，分别有94.5%和93.4%的样本被分在样本数大于10的类别中，这样就有足够的样本数据来训练预测模型。值得注意的是，层次聚类能够筛选出异常的母线负荷，有的类别中样本很少，比如表1、2中有许多类只有1个样本，这种异常的原因通常是数据采集存在错误、极端的天气影响、用户检修设备或者断路器跳闸等，本文暂不考虑这些异常。

表1 母线1全年负荷数据聚类结果

表2 母线2全年负荷数据聚类结果

根据母线1和母线2全年负荷数据聚类结果，结合历史天气和日期类型数据建立决策树如图2、3所示。

图2 母线1全年负荷分类决策树

图3 母线2全年负荷分类决策树

图2、3中，X[0]～X[4]依次代表日最高气温、日平均气温、日平均湿度、星期类型以及节假日类型。母线1中，预测日是2016年2月7日，星期日，春节的第一天，最高气温16.7度，平均气温8.4度，平均相对湿度45.4%，根据决策树查询分类规则如图2，该日为第18类，则该日母线负荷也属于第18类。母线2中，预测日是2015年12月24日，星期五，普通日，最高气温8.8度，平均气温7.3度，平均相对湿度83.7%，根据决策树查询分类规则如图3，该日为第17类，则该日母线负荷也属于第17类。选取母线1全年负荷数据聚类结果中第18类的样本数据和母线2全年负荷数据聚类结果中第17类的样本数据分别训练ELM预测模型并对两个预测日的母线负荷进行预测；传统ELM预测方法则分别选取两个预测日前30天的负荷数据来训练ELM预测模型并对两个预测日的母线负荷进行预测。预测结果对比如图4和图5。

图4 2月7日母线1负荷预测结果比较

从图6和图7中可知，HC-ELM的预测误差小于ELM，经计算可得：母线1中，HC-ELM的MAPE为2.89%，ELM的MAPE为4.33%；母线2中，HC-ELM的MAPE为4.21%，ELM的MAPE为5.73%。可见采用的新方法可以提高预测精度。

图5 12月24日母线2负荷预测结果比较

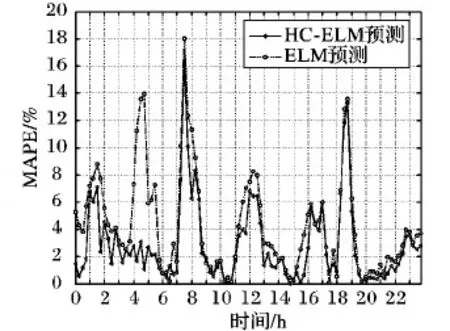
图6 2月7日母线1的MAPE值比较

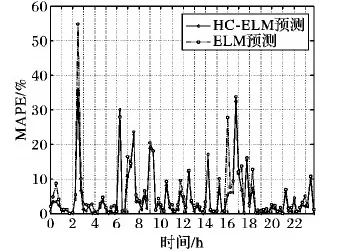
图7 12月24日母线2的MAPE值比较

为了进一步验证HC-ELM的有效性，对于母线1，预测了从2016年2月8日至2月14日连续一周的母线负荷，其中2月8日至13日为春节，14日为工作日，母线负荷预测结果比较如图8；对于母线2，预测了从2015年25日至31日连续一周普通日的母线负荷，母线负荷预测结果比较如图9。母线1、2的MAPE的计算结果如表3所示，可以看出，利用HC-ELM计算母线1和母线的MAPE的平均值比ELM分别降低了1.4个百分点和0.8个百分点。

3 结语

为了提高对母线短期预测的效果，提出一种基于层次聚类和极限学习机的母线短期负荷预测算法。本文使用层次聚类法选取了与待测日相似度更高的训练样本，弥补了传统预测算法选取的相似日与待测日特征相似度欠佳的不足。根据实验分析可知，本文提出的HC-ELM与传统算法相比，不仅提高了普通日母线负荷预测的效果，特别地，针对特殊日的母线负荷预测同样具有更高的预测精度。下一步工作要考虑负荷类型对母线负荷的影响，以及将该模型应用到Hadoop或Spark等大数据平台上。

图8 2月8日—2月14日母线1负荷预测结果比较

图9 12月25日—12月31日母线2负荷预测结果比较

%