基于改进迭代收缩阈值算法的微观3D重建方法

伍秋玉，张明新，刘永俊，郑金龙

(1.中国矿业大学 计算机科学与技术学院，江苏 徐州 221116； 2.常熟理工学院 计算机科学与工程学院，江苏 常熟 215500；3.东北大学 计算机科学与工程学院，沈阳 110819)(*通信作者电子邮箱zmxcslg@163.com)

0 引言

在微纳米计算机视觉中，基于视觉的微纳米尺度3D形貌重建，对于较全面地理解样品特性和对操作过程进行评估具有重要意义。比较常用的微观3D重建方法[1]主要有体积恢复方法、立体视觉深度恢复方法、聚焦深度恢复方法以及离焦深度恢复方法。与其他的3D重建方法相比，离焦深度恢复方法由于所需图片少、设备简单、操作便利等优点，近些年得到广泛关注与深入研究[2]。离焦深度恢复最早由Pentland[3]提出，该方法利用二维图像的离焦程度特征与景物深度之间的映射关系，反解出景物的三维深度信息[4-5]。

在景物的离焦深度恢复方法中，首先必须获取景物不同程度的离焦图像，这就导致要改变摄像机参数。但是，在微纳米图像观测中，观测空间非常有限，而且使用的是具有高放大倍数的相机，所以相机的成像模型会随着摄像机参数的改变而改变[6]。受限于微纳米观测中的条件，魏阳杰等[7]提出了一种新的基于参数固定的单目视觉摄像机的三维离焦形貌恢复方法。该方法利用相对模糊度[7-8]及热辐射方程[7,9]来求解景物的深度信息，并将深度信息的求解转化成动态优化问题来求解。

在求解离焦深度恢复动态优化问题时，文献[7]采用经典的迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm， ISTA)[10]来求解，但ISTA是梯度下降法的延伸，迭代过程仅考虑当前点的信息进行梯度估计更新迭代点，优化过程呈“之”字形[10-12]向极小值点靠近，收敛速度比较慢；而且该算法在迭代过程中采用固定步长，在靠近极小值点时，此时的固定步长可能大于实际的迭代步长，导致算法迭代效率不佳，从而使得重建的微观3D形貌精度不高。

针对ISTA求解离焦深度恢复动态优化问题的不足，本文提出了一种基于加速算子梯度估计和割线线性搜索的方法优化ISTA——FL-ISTA(Fast Linear ISTA)。该算法在ISTA的基础上加入一个加速算子，该加速算子由当前点和前一个点的线性组合构成，利用加速算子重新进行梯度估计，更新迭代点，以加快算法的迭代速度；而且为了改变ISTA迭代步长固定的限制，结合割线线性搜索寻找最优迭代步长，以提高算法的迭代效率。将FL-ISTA应用于标准500 nm尺度栅格的深度信息重建，实验结果表明，与ISTA、快速迭代收缩阈值算法(Fast ISTA, FISTA)和单调快速迭代收缩阈值算法(Monotohy FISTA, MFISTA)相比，FL-ISTA收敛速度更快，重建的深度信息值下降更快，更接近标准500 nm栅格尺度，并且相对误差、平均误差、均方差更小，有效地提高了求解离焦深度恢复动态优化问题的效率和重建的微观3D形貌的精度。

1 全局离焦深度恢复

1.1 离焦成像模型

在图像处理中，图像的模糊化通常可以用卷积的形式表示如下：

I2(x,y)=I1(x,y)*H(x,y)

(1)

其中:I1(x,y)、I2(x,y)和H(x,y)分别代表清晰图像与模糊图像以及点扩散函数，*表示卷积。根据点扩散原理，点扩散函数可由二维高斯函数来近似表示，并且其中的模糊扩散参数σ表示图像的模糊程度值。由于热辐射方程具有各向同性，所以式(1)又可以表示为：

(2)

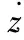
并且:

σ2=2tc

(3)

如果深度图是理想平面，那么c是一个常数，否则可以表示为如下形式:

(4)

其中▽和▽·分别代表梯度算子和微分算子：

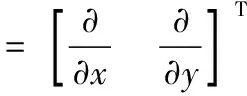
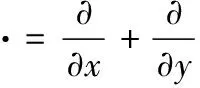
由上式可知，首先需要已知清晰图像g(x,y)来求解热辐射方程，但这是一个复杂的过程，因此，Favaro等[8]提出了相对模糊的概念。

假设有两张不同程度的模糊图像I1(x,y)和I2(x,y)，模糊扩散系数分别为σ1和σ2，并且σ1<σ2，那么I2(x,y)可以写成如下形式:

(5)

(6)

而式(4)又可以写成如下形式:

(7)

并且在Δt时刻，u(x,y,t)=I2(x,y)，Δt可被定义为:

Δσ2=2(t2-t1)c≐2Δtc

(8)

而且：

(9)

其中:ηi(i=1,2)表示模糊圆半径，而λ则表示模糊度与模糊圆半径之间的常数。

(10)

其中:v、f、s分别为摄像机的像距、焦距和物距，D为凸透镜半径。

1.2 深度信息重建

假设图像I1(x,y)是物距变化之前的离焦图像，它的深度信息为S1(x,y)，而图像I2(x,y)是物距变化之后的离焦图像，它的深度信息为S2(x,y)，已知理想焦距为s0，在这一部分，图像I2(x,y)的深度信息是由物距变化ΔS来获得，原理示意图如图1所示。

首先由以上条件建立热辐射方程:

(11)

其中相对模糊度又可以表示为:

(12)

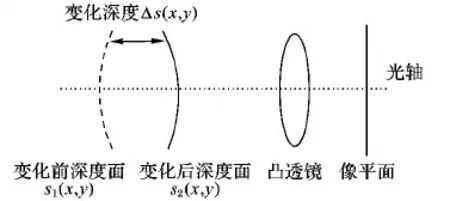
图1 深度信息原理图

本文定义:

(13)

因此，最终的深度信息为:

(14)

为了更好地解决离焦深度恢复动态优化问题，建立如下目标函数来计算热辐射方程:

(15)

由于上述的求解过程可能是病态的，所以在目标函数最后加上一个Tikhonov正则项，表示为:

ρ‖▽s2(x,y)‖2+ρl‖s2(x,y)‖2

(16)

上式第三项是关于深度图的平滑约束，第四项是保证深度图的有界性，实际上能量系数ρ>0，l>0。损失的能量表示为:

E(s)=∬(z(x,y,Δt)-I2(x,y))2dxdy+

ρ‖▽s‖2+ρl‖s‖2

(17)

因此，可以通过求解如下优化问题来求解景物深度信息:

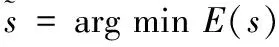
(18)

s.t. (11)和(14)

2 FL-ISTA

2.1 ISTA求解离焦深度恢复动态优化问题

对于1.2节中的离焦深度恢复动态优化问题，采用ISTA进行求解，令

E1(s)=∬(z(x,y,Δt)-I2(x,y))2dxdy

(19)

于是，对于无约束最优化问题:

E1(s)=∬(z(x,y,Δt)-I2(x,y))2dxdy

解决上式的梯度算法为:

sj=sj-1-tj▽E1(sj-1)

(20)

其中tj表示迭代步长，而上式的二阶估计模型可以表示为:

sj=arg min{E1(sj-1)+▽E1(sj-1)(s-sj-1)+

(21)

当式(19)加入Tikhonov正则项，即:

E(s)=E1(s)+ρ‖▽s‖2+ρl‖s‖2

可以得到以下迭代公式:

sj=arg min{E1(sj-1)+▽E1(sj-1)(s-sj-1)+

(22)

忽略常数项，可以得到:

(23)

由于Tikhonov正则项是可分的，因此sj的计算可以变成解决每个元素的一维问题，它的迭代公式为:

sj=Tρtj(sj-1-tj▽E1(sj-1))

(24)

其中Tρ:Rn→Rn是收缩算子，定义为:

(25)

2.2 利用加速算子进行梯度估计

ISTA是梯度下降法的一种延伸，每次迭代只是利用当前点的信息进行梯度估计，更新迭代点，算法迭代速度一般。基于此，在ISTA的基础上引入加速算子，首先加速算子由当前点和前一个点的线性组合构成，然后利用加速算子重新进行梯度估计求出下一个迭代点，加速算子表示为：

yj+1=sj+aj(sj-sj-1)

(26)

其中:sj、sj-1分别代表当前深度信息值和前一次深度信息值；sj-sj-1表示搜索方向；aj表示由当前深度信息sj开始，沿着sj-sj-1所构成的搜索方向进行迭代所需要的步长因子；而yj+1表示由当前深度信息sj开始，沿着sj-sj-1所构成的搜索方向进行步长为aj所得到的深度信息。利用加速算子重新进行梯度估计的示意图如图2所示。

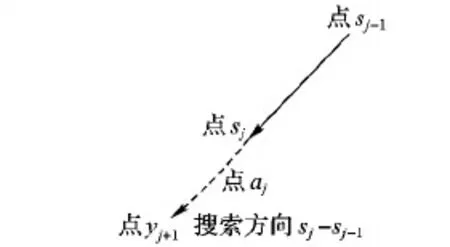
图2 加速算子梯度估计示意图

在ISTA的基础上，引入加速算子重新进行梯度估计求出下一个迭代点，因此式(24)可以写成以下形式：

sj+1=Tρtj(yj+1-tj▽E1(yj+1))

(27)

2.3 割线线性搜索寻找最优迭代步长

由于ISTA在迭代过程采用固定步长，优化过程在靠近极小值点时，此时固定步长可能大于实际迭代步长，导致算法效率不佳；因此，采用线性搜索改变固定步长的限制。线性搜索主要有牛顿法、黄金分割法、割线法等，其中牛顿法收敛的条件是初始点充分靠近某一极值点，黄金分割法在求极值时需要事先确定搜索区间，而割线法能很快求出初始点附近的极值点，所以，采用割线线性搜索寻找最优迭代步长，提高算法效率。

2.3.1 割线线性搜索

割线法的迭代公式表示如下：

(28)

其中:x(k)、x(k-1)是两个初始点，x(k+1)是迭代后求出的点;f′(x(k-1))、f′(x(k))是x(k)、x(k-1)的导数值，其迭代过程如图3所示。

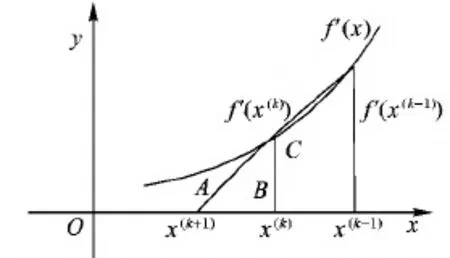
图3 割线线性搜索示意图

2.3.2 寻找最优迭代步长

为了求解最优迭代步长，建立以下关于步长的一元函数：

t*=arg minψ(t)

(29)

其中：

ψ(t)=∬(z(x,y,Δt)-I2(x,y))2dxdy+

ρ‖▽(s+td)‖2+ρl‖s+td‖2

(30)

其中：ψ(t)是关于t的一元函数，t是迭代步长，d是迭代方向，t*是最优迭代步长，因此可以采用一维线性搜索方法来求极小值。

对于式(30)采用割线迭代格式表示为：

(31)

将利用割线线性搜索计算得到的最优迭代步长t*代入式(27)，此时可以写成以下形式：

(32)

FL-ISTA针对ISTA迭代步长固定的限制，引入割线线性搜索寻找最优迭代步长，动态确定每次最优迭代步长，该方法首先以大步长快速收敛到理想解附近，然后再以小步长逼近最优解，从而提高算法效率。

3 算法流程

FL-ISTA步骤如下所示，算法流程如图4所示。

步骤1 给出摄像机参数：焦距f,相距v,理想物距s0，凸透镜半径D,模糊度与模糊圆之间的常数λ，两幅模糊图像I1、I2，能量阈值ε，能量系数ρ，迭代步长t0，y1=s0,j=1，n1=α1=1, 0<αk<1。

步骤2 初始化深度信息为s0。

步骤3 计算式(12)，得到相对模糊度Δσ2。

步骤4 计算式(11)，得到扩散方程的解z(x,y,Δt)。

步骤5 用步骤4所得的解来计算能量式，如果能量小于阈值ε，则停止，此时的深度信息即为所求；否则，转入步骤6。

步骤8 将步骤7所得到的yj+1代入式(27)。

步骤9 利用割线线性搜索求出最优迭代步长t*，代入式(32)，求出此时的sj+1。

步骤10 将计算所得的sj+1代入式(14)，更新深度，回到步骤3，继续迭代。

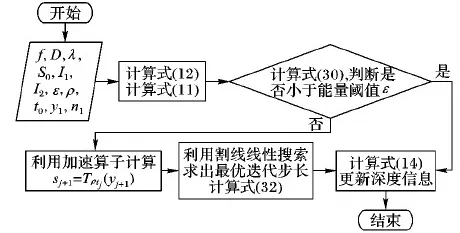
图4 FL-ISTA流程

4 实验结果及分析

为了验证本文所提算法在求解离焦深度恢复动态优化问题的正确性和有效性，分别采用ISTA、FISTA和MFISTA以及本文提出的FL-ISTA对标准500 nm尺度栅格进行深度信息重建实验。标准纳米尺度栅格高500 nm、宽1 500 nm。实验中使用的是HIROX-7700显微镜，放大倍数为7 000，其余的摄像机参数为：焦距0.357 mm，理想物距3.4 mm，光圈大小为2。在配置为Intel i5-4900酷瑞双核，主频为3.3 GHz，内存为8 GB的计算机上用Matlab 2012a对标准500 nm栅格进行实验。

对标准500 nm尺度栅格的处理结果如图5～8所示。其中：图5是栅格的两幅离焦图像，图5(a)是深度信息变化前的离焦图像，图5(b)是深度变化后的离焦图像；图6为标准500 nm尺度栅格的真实形貌；图7是深度信息值收敛曲线；图8(a)～(d)分别为ISTA、FISTA、MFISTA和FL-ISTA处理标准500 nm尺度栅格的3D形貌恢复结果。图中，平面坐标的单位是像素，像素的大小为115.36 nm×115.36 nm，纵坐标的单位是mm。

图5 栅格的离焦图像

图6 真实的栅格3D形貌

根据文献[7]的实验结果，将能量阈值ε设置为2，能量系数ρ设为0.2。在此条件下，ISTA、FISTA、MFISTA在迭代200次左右趋于收敛，而FL-ISTA在小于200次内就已经开始收敛，为了便于比较，设置迭代次数为250，如图7为四种算法250次内迭代深度信息值收敛曲线。由图7可以看出，在迭代初期，四种算法都能以较快的速度收敛，属于正常现象。但是由于在离焦深度恢复动态优化问题中，FL-ISTA在ISTA的基础上，利用当前点和前一个点的线性组合构成加速算子，重新进行梯度估计，加快迭代速度；引入割线性搜索寻找最优迭代步长，提高了算法效率。由60～120次的迭代过程中明显可以看出，FL-ISTA得到的深度信息值下降最快，并且趋于收敛时得到的深度信息值相对较小，此时更加接近真实的标准500 nm栅格尺度，使得恢复出来的3D形貌尺度更精确。

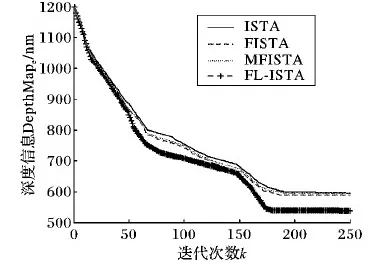
图7 四种算法深度信息值收敛曲线

由图8(a)～(d)可以看出，四种算法重建的3D形貌，尽管在边缘处误差稍微大，但重建的3D形貌大致符合标准500 nm尺度栅格的整体形貌。从重建的3D形貌明显看出，前三种算法重建的3D形貌中深度信息值相差不大，分别为600 nm、590 nm、590 nm左右，而FL-ISTA中深度信息值明显下降很多，深度信息值为540 nm左右，更接近标准500 nm栅格尺度，使得恢复出来的3D形貌更精确。并且，在相同的条件下，四种算法对标准纳米尺度栅格进行深度重建，经多次实验结果表明，ISTA、FISTA、MFISTA深度重建平均运行时间分别为105 s、105 s、100 s左右，而本文FL-ISTA的平均运行时间仅为30 s左右，一定程度上提高了算法的效率。

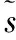
(33)

(34)

(35)

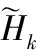
图8 四种算法重建的3D形貌

由如图9(a)～(d)可以看出，ISTA、FISTA、MFISTA所得的相对误差曲面变化不大，最大相对误差为80 nm、70 nm、70 nm左右，但是从FL-ISTA的相对误差曲面来看，最大相对误差只有20 nm左右，适合相对误差较小的微纳米操作场合。

图9 四种算法的尝试误差曲面

由图10可以看出，ISTA、FISTA和MFISTA均方差分别为0.05、0.048、0.045，而FL-ISTA均方差为0.041，与ISTA相比均方差下降了18个百分点，与FISTA和MFISTA相比均方差也较小，因此，FL-ISTA重建的微观3D形貌尺度误差相对稳定。因为对于像细胞等样品的观测与测量，重建的3D形貌尺度与真实的3D形貌尺度误差过大或过小，会导致对样品尺度的估计不准确，进而可能造成操作过程中对样品的破坏，从而造成严重后果。

由式(35)可以得出，ISTA、FISTA和MFISTA重建3D形貌平均误差分别为161 nm、160 nm、158 nm，而FL-ISTA平均误差仅为96 nm，与ISTA相比平均误差下降了40个百分点，与FISTA和MFISTA相比平均误差也较小，FL-ISTA重建3D形貌尺度与真实3D形貌尺度相差不大，可以利用重建3D形貌尺度来估计真实3D形貌尺度，以便于显微镜下对样品的操作。

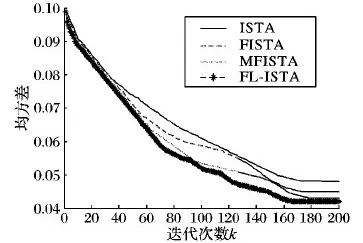
图10 四种算法均方差的收敛曲线

最后为了更好地检验本文算法的性能，分别利用ISTA和FL-ISTA对于导电探针进行深度信息恢复实验，如图11为导电探针的离焦图像，图11(a)为深度变化前的离焦图像，图11(b)为深度变化后的离焦图像；图12为处理导电探针的实验结果。

由图12可以看出，FL-ISTA恢复的形貌与ISTA恢复的形貌有明显的不同，并且在相同的条件下，经过多次实验可以得出，ISTA恢复形貌所需平均运行时间为180 s左右，而FL-ISTA恢复形貌所需平均运行时间仅为110 s，大大提升了算法的效率。

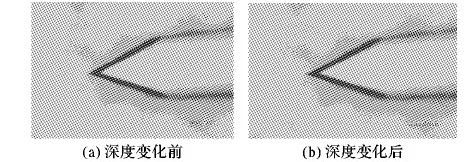
图11 导电探针的离焦图像

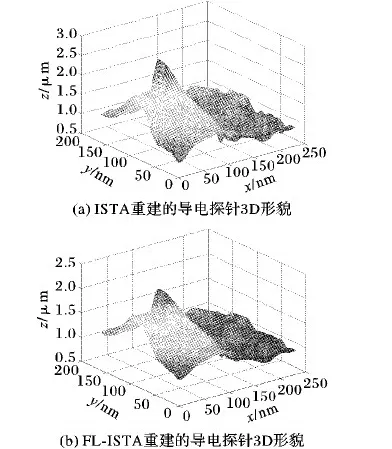
图12 ISTA和FL-ISTA重建的导电探针3D形貌

5 结语

本文提出的FL-ISTA针对ISTA求解离焦深度恢复动态优化问题迭代效率不佳，使得重建3D形貌精度不高的缺点进行优化改进，利用加速算子重新进行梯度估计，更新迭代点；结合割线线性搜索寻找最优迭代步长，提高算法效率。基于标准500 nm尺度栅格的实验结果表明，与ISTA、FISTA、MFISTA相比，FL-ISTA的收敛速度更快，它恢复的3D形貌深度信息下降更快，相对误差、均方差、平均误差更小，更接近标准500 nm栅格尺度，有效地提高了求解离焦深度恢复动态优化问题的效率和微观3D形貌重建的精度。由于在迭代过程采用割线线性搜索来寻找最优迭代步长仍需一段时间，所以接下来会进一步探索非线性搜索方法来提高算法效率。