爆破开挖振动下既有大型储油罐的动力响应*

陈 洋，吴 亮，许 锋，鲁 帅

(1.中铁港航-武汉科技大学爆破技术研究中心，湖北 武汉 430065;2.武汉科技大学理学院，湖北 武汉 430065)

大型立式钢制浮顶储油罐是储油基地广泛采用的储油容器，由于规模庞大，一旦发生破坏，后果不堪设想,为确保安全，对储罐进行应力分析、动力性能、破坏机理等方面的研究十分必要。在储油罐应力分析方面，陈志平等[1]结合长、短圆柱壳法的优点，提出了更精确的组合圆柱壳法。张云峰等[2]建立了储油罐三维地震响应的力学计算模型，并进行了储油罐三维地震响应的数值分析，发现竖向地震分量引起的水平加速度和基底剪力在总加速度和总基底剪力中占有较大比重，在储罐抗震设计中必须考虑竖向地震的作用。孙建刚等[3]的储罐三维地震反应振动台模型实验也证实了立式浮放储罐抗震设计中需要考虑三维地震作用。另外，孙建刚等[4-5]在储油罐的隔震方面做了较系统的研究，建立了考虑摆动效应的立式储罐隔震分析简化力学模型，并将数值计算结果与无摆动效应隔震模型的计算结果进行比较分析，结果表明，基底隔震装置能有效降低大型储罐的基底剪力，但对液面晃动波高的影响不大。

由于地形原因，储油基地后续扩建工程的基础需要爆破开挖。王开志等[6]根据现场环境，设计了某部储油罐基础的爆破开挖方案，优化了布孔方式和炮孔参数，并成功实施了爆破。关于爆破开挖扰动对既有储罐影响的研究尚未见报道。本文中以某石油储备基地扩建项目中的实际问题为背景，基于ANSYS/LS-DYNA的隐式-显式顺序求解技术，结合流固耦合算法，采用数值模拟方法研究爆破振动下大型储油罐的动力响应，分析动应力在结构体中的传播与分布规律，研究储油罐结构的响应及其稳定性。

1 基于ANSYS/LS-DYNA的隐式-显式顺序求解方法

在许多工程中，结构的初始应力对结构动力响应的影响是不能忽略的。如带有初始压力的压力容器、高地应力条件下的开挖、螺栓连接动力响应等，在进行动力响应分析时，都应考虑结构初始应力的影响。大型储油罐的动力响应也是如此，在数值模拟时，重力影响是不可忽略的。LS-DYNA作为国际上最著名的显式动力分析程序，用来分析爆炸与冲击、结构碰撞、金属加工成型等高度非线性的瞬态动力学问题是非常有效的。在处理静态问题(如结构的自重、初始应力)时，LS-DYNA显式求解器可以通过添加人工阻尼，运用动力松弛的方式施加载荷，运用显式求解器近似求解静态或准静态问题。但是这样处理得到的结果无论是精度还是效果，都不如隐式求解器计算的结果。ANSYS的隐式方法在处理静态问题尤其是线性问题时，有极大的优势。因此，结合隐式与显式求解器的优点，运用隐式-显式顺序求解方法分析结构在初始载荷作用下的动力响应问题是比较理想的。即在进行显式动力分析之前，用隐式求解器对结构的预载进行分析，然后以预载的结果为初始状态进行动力响应的显式分析。基于ANSYS/LS-DYNA隐式-显式顺序求解方法分析储油罐爆破振动响应的基本思路如图1所示。

2 爆破载荷的等效处理

根据文献[7]，计算中可以将爆破荷载做适当简化，其中一种简化方式是将爆破荷载均匀分布在同排炮孔连心线所在竖直面上。如图2(a)所示，半径为r0的炮孔壁上压力为p0，孔间距为L，则可以将载荷等效施加在如图2(b)所示的炮孔连心线上。等效压力为：

pe=(2r0/L)p0

(1)

式中：p0可以根据C-J爆轰条件和爆腔膨胀理论确定。这种简化方式可以从圣维南原理得到合理的解释，因此工程中合理运用此方法是可以接受的。

3 工程实例的数值模拟

3.1 工程概况

某石油储备基地已有50座10×104m3的储油罐，依山而建。其扩建项目规模为300×104m3，拟建10×104m3钢制单盘式外浮顶储罐30座。其中两座拟建设储罐的地基需要爆破开挖。为研究爆破振动对既有储罐的影响，对相邻的油罐及其地基进行有限元分析，模型外形设计参数如图3所示，储罐管壁设计参数及材料类型如表1所示。

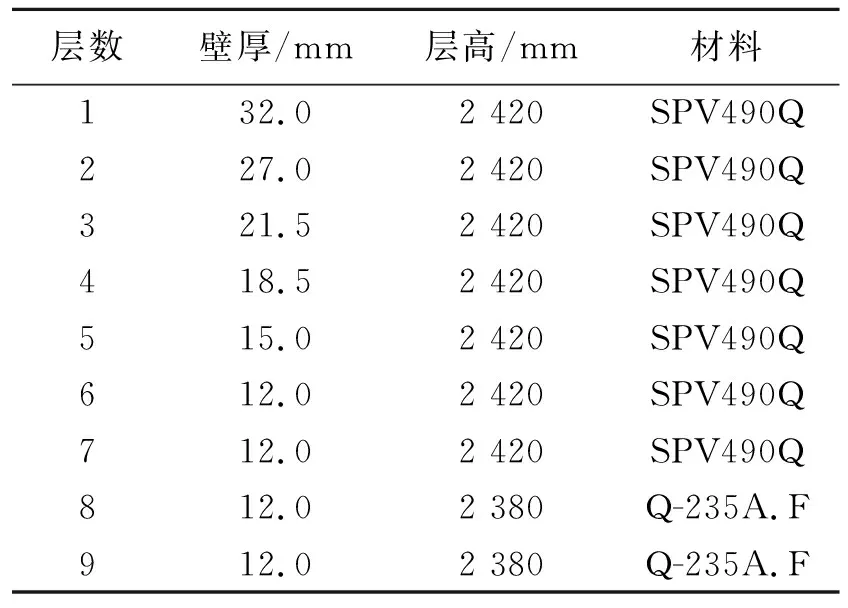
层数壁厚/mm层高/mm材料132.02 420SPV490Q227.02 420SPV490Q321.52 420SPV490Q418.52 420SPV490Q515.02 420SPV490Q612.02 420SPV490Q712.02 420SPV490Q812.02 380Q-235A.F912.02 380Q-235A.F

如图3所示，在地基边缘爆破，柱状装药长度为6 m，孔径50 mm，药径30 mm，孔距1 m，爆破位置距罐壁20 m。在此距离下，研究爆破振动对储油罐的影响，可以忽略爆破载荷的分布情况[7]，从而运用上述简化方式，将爆破载荷简化成作用在同排炮孔连心线所处的一块10 m×6 m的竖直面上的均布载荷。压力峰值约5 MPa，采用正弦波波形进行分析，作用3个周期。

3.2 有限元模型建立及材料模型

3.2.1 单元类型

运用LS-DYNA进行显式动力学分析时，流体拟采用ALE算法，固体拟采用Lagrange算法。solid164单元是用于显式动力分析的8节点三维实体单元，在使用上没有特殊限制，既可用Lagrange网格，也可用ALE网格，故地基、罐内液体和空气采用solid164单元。shell163单元是用于显式动力分析的4节点薄壳单元，在模拟储油罐罐壁这类薄壳或薄膜结构中被广泛运用，并取得较好的效果，故钢制储罐采用shell163单元模拟。隐式单元与显式单元的相互转换中存在对应关系，solid164单元对应于solid185单元，shell163单元对应于shell181单元。当所用的隐、显式单元不对应时，需要手动修改参数转换。因此，在隐式静力分析中分别采用solid185、shell181单元模拟地基和钢制储罐，在随后显式动力分析中自动转换成对应显式单元。罐内液体和空气采用fluid80单元，随后手动转换成solid164单元。

3.2.2 网格划分

在进行有限元模拟的时候，当所用单元为8节点实体单元或4节点壳单元，划分网格时一般不宜采用退化的四面体或三角形单元。为保证网格质量，对模型进行适当剖分，采用映射的方式划分网格。同时，为了保证ALE算法有效进行，划分网格要保证液体网格和空气网格一致。流体与固体之间的相互作用通过LS-DYNA的流固耦合关键字实现。网格尺寸的控制兼顾计算精度和计算效率。通过试算，网格最大尺寸控制在2 m时有较高的计算效率，且计算精度满足工程要求。最终一共划分了142 976个单元。有限元模型如图4所示。

3.2.3 材料模型及参数

(1)钢制储罐材料本构模型

考虑储罐材料的非线性特性将导致储罐结构动力响应的非线性，采用双线性随动强化材料模型(BKIN)模拟储油罐钢材，该模型弹塑性材料的本构关系通过两段斜率不同的直线段来模拟，其应力应变关系如图5所示。需要定义的基本参数如表2所示。

(2)地基岩体本构模型

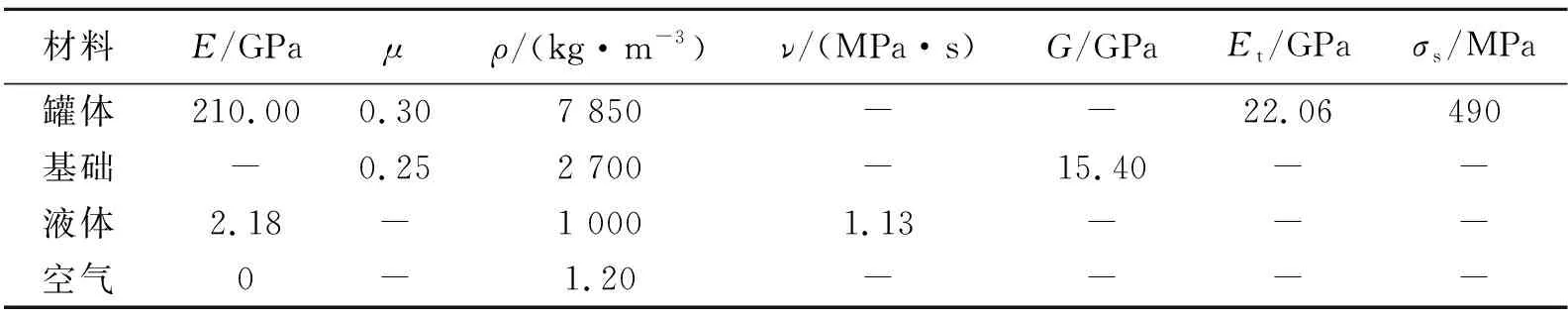
表2 材料基本参数Table 2 Basic parameters of the materials

Drucker-Prager(D-P)模型是一种广义的Mises理想塑性模型，这种材料模型能有效模拟土壤、岩石以及混凝土等材料，这里采用该模型来模拟地基岩体。在LS-DYNA中用*MAT_DRUCKER_PRAGER关键字定义。除表2给出的参数外，还需定义的主要参数有：摩擦角为0.872，破坏面形状参数为1.0，黏聚力为1.5 MPa，最小抗剪强度因子为0.05。

(3)液体和空气模型及状态方程

液体和空气均采用LS-DYNA中的NULL流体材料模型。输入的基本材料参数见表2。液体单元采用Grüneisen状态方程描述，对于压缩材料和膨胀材料，其压力分别为：

(2)

膨胀材料p=ρ0C2μ+(γ0+αμ)E

(3)

式中：C=1 480，S1=2.56，S2=-1.986，S3=0.226 8，γ0=0.5，α=0，E=0。空气单元压力采用线性多项式状态方程模拟，压力由下式给出：

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(4)

式中：C0=-1×105，C1=C2=C3=C6=0，C4=C5=0.4。

3.3 计算结果分析

3.3.1 罐壁上不同位置的振速

对爆破载荷为25 Hz的工况进行数值计算。图6(a)～(b)分别是罐壁正面0、2.42、21.80 m(由后文中质点振动速度沿高度的分布曲线可知，2.42 m处是罐壁上水平质点振动速度出现突增的点，而0 m和21.80 m处分别是罐壁底部和顶部节点，此3点均为较特殊的点，故此处选择此3点输出质点振动时程曲线)处x和z方向的质点振速时程曲线。从图中可以看出，不同高度的振速曲线的每一个波峰(谷)基本是按照由罐底向上的顺序依次出现，爆破振动的影响沿着罐壁由底部逐渐传播到储罐顶部。

图7是罐壁正面x方向质点振动速度沿高度的变化曲线。总体上看，在满载、半载和空罐情况下，罐壁顶部水平方向(x方向)质点振动速度较底部有一定的衰减，这与以往所认识的高层结构对地震的放大作用[8]有所不同。分析可知，这有两方面原因：其一，文中所研究的大型立式圆柱储油罐高径比偏小，其纵向比较稳定，在振动响应中基本不会出现整体的摆动，由其模态振型分析可知，其主要振动形式为罐壁的环向多波振型[9]，因此不会产生顶层放大效应；其二，与天然地震波相比，爆破地震波频率高、持续时间短[10]，而高频振动在传播过程中幅值衰减较快，传播到顶部时无放大效应，这与文献[11]的结论是一致的。进一步分析图7可知，在液面以下的位置，储罐内壁与罐内液体接触的部分水平方向质点振速都较小，而离开液面以上的位置，罐壁水平质点振速迅速增大到较大值，随后继续随高度增加缓慢减小。这说明罐内液体对与之接触的罐壁的质点水平振动能起到一定的缓冲作用。图8是罐壁正面z方向质点振动速度沿高度的变化曲线。z方向振速随高度上升而增大，竖直方向振速仍符合放大效应。

进一步研究振动响应沿罐壁圆周的传播情况。分别在2.42 m的位置和顶部沿罐壁圆周均匀的选取9个测点，测点在罐壁圆周上的位置如图9所示。图10分别是x、z方向的振速沿罐壁圆周的分布情况。从图10中可以看出，从测点1到测点9，x和z方向振速基本呈现出逐渐衰减的趋势，说明爆破对储油罐的影响从正面到背面逐渐减弱。

3.3.2 罐壁上的应力分布情况

大型立式圆柱钢制储油罐在地震中罐壁底部易产生“象足”变形[12]，进而导致严重的破坏情况。现有的研究资料已经证实这种“象足”变形是由于罐壁上的轴向压应力过大，导致罐壁局部失稳产生的屈曲破坏，而非工作应力超过强度极限产生的强度破坏[12-14]。研究爆破振动下储油罐罐壁上的应力分布情况有助于找到爆破开挖过程中罐壁上的薄弱点。图11是罐壁上的应力沿高度的分布情况，由图11可知，罐壁3 m以下的位置轴向应力较大，达到15 MPa以上，而上部轴向应力都比较小。环向应力与Mises应力的分布情况基本一致，最大值均出现在3 m左右的位置。

图12是罐壁上高度3 m左右位置的应力沿罐壁周向的分布情况。由图12可知，应力从正面沿着周向到背面明显衰减，最大轴向压应力和最大Mises应力在正面，即迎爆侧。由罐壁上应力分布情况可知，在爆破开挖过程中，既有储罐罐壁迎爆侧高度为3 m左右的位置应力较大，是薄弱环节，最易发生“象足”屈曲。

3.3.3 储油罐的响应与罐内液面高度的关系

为了研究不同储液量情况下储罐的响应情况，分析了罐内液面高度从0 m(空罐)到20 m(满罐)的罐壁顶部质点振动速度，图13是x和z方向质点振速与罐内液体液面高度的关系。其中z方向振速随液面高度增加而增大，且增幅较小。x方向振速随液面高度增加先略有减小，在液面高度为5 m时最小，低于1.5 cm/s，然后随液面高度继续增加而增大，到储液接近满罐时达到最大。由图13可知，该储油罐在储液高度不高于10 m的情况下，水平和竖直方向质点振动速度均低于2 cm/s，根据最新的《爆破安全规程(GB 6722-2014)》，这低于工业和商业建筑物的安全允许质点振动速度，为确保邻近既有储罐的安全，爆破施工过程中邻近储罐储液高度应不高于10 m，即保证处于半载及以下的状态。

3.3.4 不同频率爆破载荷下储油罐的响应

影响爆破地震波频率的因素是多方面的。实验表明，爆破振动的优势频率随装药量的增大而降低，同时，炸药的爆速越高，爆破地震波主频越高；另外，随着传播距离的增加，振动的高频部分衰减较快，而低频部分基本保持不变，从而爆破振动的优势频率也会降低。装药深度对频率也有很大影响，深孔爆破产生的地震波主频较低，浅孔爆破产生的地震波主频较高。实际工程中的岩性与地形条件、爆破方式、装药结构等，也是影响爆破振动频率的重要因素。同振动强度一样，爆破振动的频率特性也对结构的破坏起到决定性作用。爆破振动主频与结构的固有频率越接近，由于共振效应，结构物的响应越剧烈，当达到一定频率时，这种影响基本消失[15]。同时，文献[10]中已经指出，爆破地震主频率大都在10～30 Hz，有的高达50 Hz以上，与普通工程结构的自振(基振)频率相比，它高得多。表3是本文中计算的储油罐前20阶流固耦合模态、空罐模态和文献[9]的值。空罐模态模拟值与文献值吻合。模拟得到的储油罐前20阶流固耦合模态频率在0.5 Hz以下，远低于爆破地震波的主频。

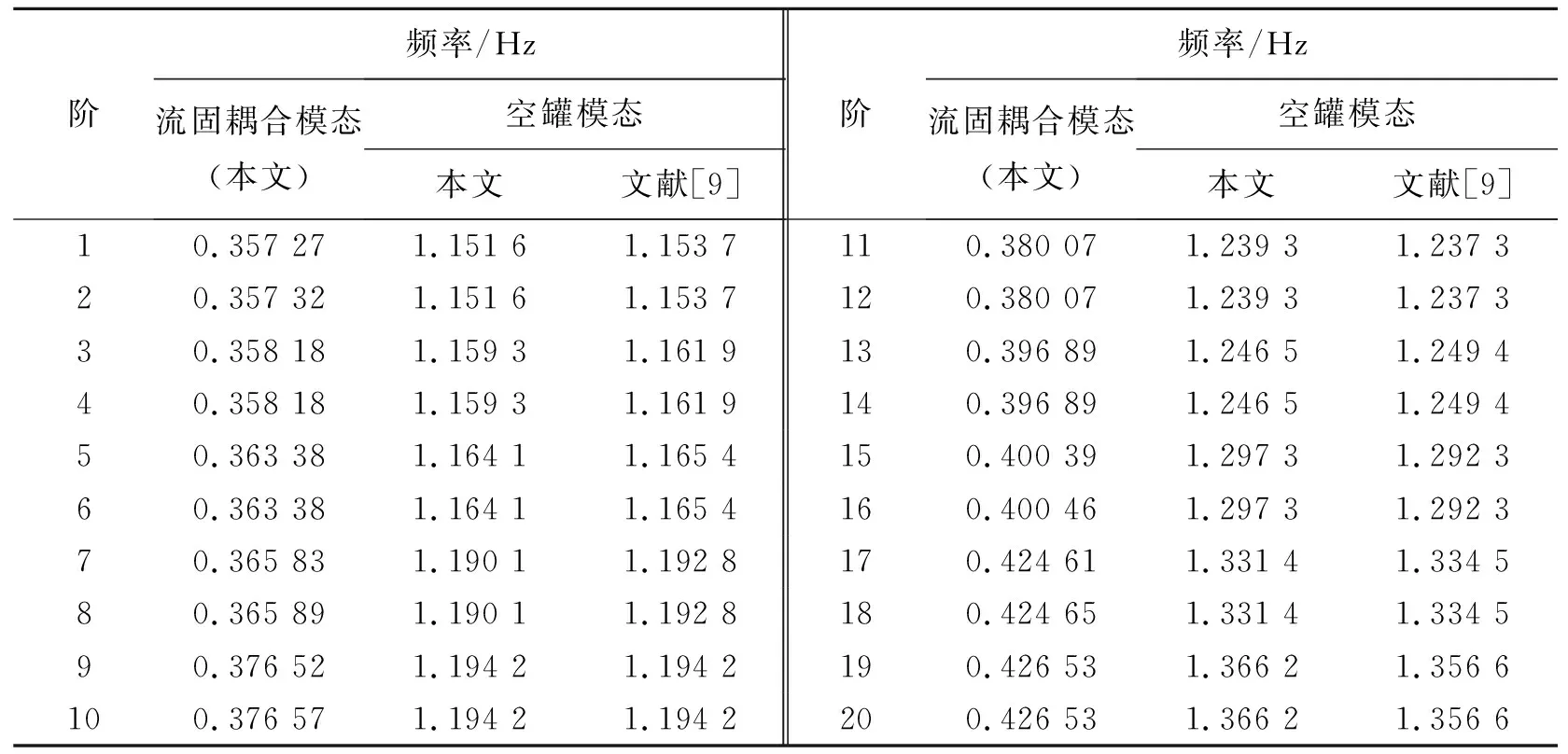
表3 储油罐前20阶模态Table 3 The first 20 modes of storage tank

本文中还计算了频率从5 Hz到100 Hz(间隔为5 Hz)的载荷作用下储油罐的响应。图14是罐壁迎爆侧顶部节点的x方向振速与载荷频率的关系。由图14可知，载荷频率在30 Hz以下时，x向振速随频率升高急剧增大，在30～70 Hz之间，x向振速基本稳定在3 cm/s左右，载荷频率超过70 Hz时，x向振速随频率升高逐渐减小，从85 Hz开始，振速又基本平稳在2.5 cm/s左右。图15是罐壁正面顶部节点的z方向振速与载荷频率的关系。从图中可以看出，在80 Hz以下，z方向振速随频率的升高而增大，80 Hz以上，略有减小，但基本稳定在11.3 cm/s左右。这说明在爆破振动主频范围内，远大于储油罐固有频率条件下，罐壁上质点振速随着爆破振动频率的降低呈减小趋势。由于储油罐基频远低于爆破载荷主频，共振效应的影响基本消失，此时不能用“爆破震动主频与结构的固有频率越接近，结构物的响应越剧烈”这一结论分析储油罐的响应与载荷频率的关系,而应该从其他与频率相关的因素上研究储油罐随载荷频率变化的响应规律，例如文献[16]中提到的波形叠加效应等因素，这是后续研究应着重关注的地方。

4 储油罐爆破振动安全评估

与天然地震波不同，爆破地震波是局部振动，且幅值大、衰减快、频率高、持续时间短。当遇到超大、超高型构筑物，如本文中所研究的大型原油储罐，爆破扰动首先引起迎爆侧距爆源最近的点振动，随后在结构内部向周围传播。由于大型储油罐的振型主要是环向多波振型，并且高频振动的幅值衰减快，因此罐壁顶部水平方向质点振速无放大效应，反而较底部有一定的衰减。所以罐壁顶部水平方向质点振动速度仅能在一定方面反映爆破扰动对储油罐的影响程度，而不能以此判断储油罐是否安全。此外，由于罐内液体对液面以下罐壁质点振动有一定的缓冲作用，导致罐壁质点振速的分布情况较为复杂，所以从罐壁质点安全振速方面来考察储油罐的危险点有一定的困难。而爆破过程中，罐壁应力分布情况较为明晰，导致“象足”破坏的最大轴向压应力在罐壁迎爆底部，并且环向应力和Mises应力最大值也出现在迎爆侧高度为3 m左右的位置。因此，对此处罐壁进行应力监测，能有效反映储油罐整体结构爆破振动的安全性。按照美国APl650的罐壁轴向压应力许用值计算公式[12]，计算得到本文中所研究的储罐罐壁轴向许用压应力为33.12 MPa。对满载的储油罐在25 Hz的载荷作用下的工况进行数值计算得到的爆破振动下储油罐罐壁最大轴向压应力为23.71 MPa，因而这种工况下储油罐是安全的。

此外，除了考虑储油罐整体结构的爆破振动安全外，储油罐的其他附属设施，例如浮顶运行装置、阀门结构、监测仪器以及管道与罐体连接部位等也是需要考虑的。

5 结 论

经过用隐式-显式顺序分析方法对在距离罐壁水平距离为20 m处开展的爆破施工工程实例进行数值模拟，得到以下认识：

(1)该工程爆破振动下，大型储油罐罐壁顶部水平方向的质点振动速度没有放大效应，振动传播到顶部时有一定的衰减。由于爆破振动载荷特点和储油罐的结构特点，罐壁质点振速分布情况较复杂，因此罐壁顶部质点振速能在一些方面反映爆破振动对储油罐的影响程度，但不宜以局部质点振动速度考察储油罐的爆破振动安全性;

(2)爆破振动下储油罐罐壁迎爆侧底部是薄弱环节，本文所研究储油罐的危险点在迎爆面高度为3 m左右的位置。用美国APl650的罐壁轴向压应力许用值计算公式核算该储油罐罐壁可知本文工况是安全的;

(3)爆破施工中，减小储罐储液量能有效减小爆破振动对储油罐的影响，邻近储罐储液高度不宜高于10 m;

(4)在爆破振动主频范围内，载荷频率远大于储油罐固有频率条件下，罐壁上质点振速随爆破振动频率的降低呈减小趋势。这与以往所认知的“爆破震动主频与结构的固有频率越接近，结构物的响应越剧烈”有所区别。后续工作中还需从波形叠加效应等因素上深入研究储油罐的响应与爆破振动频率的关系，建立爆破载荷频率与储罐响应程度之间的力学模型。另外，仍需根据现场测试数据进一步验证数值模拟的结果，为此类工程提供更加可靠的支撑。