基于Memetic算法的要地防空兵力机动部署优化方法*
2018-10-16赵鹏蛟李建国李红霞冯培伦
赵鹏蛟,李建国,李红霞,冯培伦
(1.北方自动控制技术研究所,太原 030006;2.解放军驻二○七所军事代表室,太原 030006)
0 引言
防空兵力部署是防空作战筹划的一项重要研究内容,兵力部署优化是指在满足一定约束条件下,合理部署各型防空武器于防御区域,使得防空武器系统的综合防御效能最大[1-2]。
现有研究主要集中于防空作战前的防空兵力筹划静态部署。但是现代防空作战战场态势瞬息万变,攻防对抗激烈,空袭方常采取较灵活的攻击策略,随着防空作战的进行,势必会发生防空火力损毁、空袭主攻方向改变、保卫目标重要程度改变等情况,原防空武器部署阵型无法发挥出体系最佳的防御效能,已不适应防空作战的需求。现役要地防空武器型号众多,在各型防空武器梯次配置的同时,可利用防空武器较强的机动能力进行战场机动来调整现有防御阵型,以最大化防空武器系统整体防御效能。
机动部署既要考虑机动后在当前战场态势下对敌整体防御效能,又要考虑前后部署阵型转换的机动距离和时间等约束,以确保在敌下一轮空袭前完成部署。近年来针对该问题的研究成果较少。文献[3]利用虚拟力算法机动部署火力单元,当有火力单元毁损时其他火力单元在虚拟力的作用下机动到新的位置以达到防御效能最优,但没有考虑机动的时间、距离等约束。文献[4-5]考虑了机动部署的调整时间约束和部署后的防御效能最大,但该文献假设防空态势未发生改变,原部署阵型是较优的,从而尽可能缩短新部署阵地与原部署阵地之间的相对位置变化。
针对目前防空兵力机动部署研究的不足,结合陆军防空兵防空机动作战的实际需求和现有防空武器装备现状,本文提出了多型防空武器混合部署机动作战的方法,将防区离散化提取候选部署阵地得到部署方案集,描述了基于战场实时态势的部署方案优化目标,并将机动距离作为约束,建立了要地防空混合火力机动部署优化模型,并利用Memetic算法优化求解。仿真算例验证了所提优化模型和算法的有效性和合理性。
1 问题的数学描述
1.1 候选部署阵地确定
现代空袭作战呈现出非对称、非线性、防区外精确打击等特点,空袭方不再采取临空轰炸的模式,而是通过投射远程精确制导弹药对目标进行远程精确打击,当载机与空袭目标的距离满足机载武器对地攻击射程(投弹圈)时,即投弹返航。针对这一新的作战样式,建立两层防线,将中程防空武器部署于投弹圈之前构筑外层防线,歼敌载机于投射精确制导弹药之前;将近程防空武器部署在安全线之前构筑内层防线,拦截敌机突防成功后投射的精确制导弹药。内层防线和外层防线之间的距离须满足接力射击的要求[6],即
式中,tp为外层防线拦截效果的评估时间;tr为内层防线防空武器的平均射击时间;V为制导弹药的飞行速度。
将近、中程防空武器随机部署在各自防线内形成多套部署方案,可通过比较各部署方案的整体防御效能来优化防空部署。文献[7]中通过网格对部署区域分割,并将交叉点作为待部署区域的备选部署点,同时依据所在点的地形等环境条件来对交叉点进行取舍,如图1所示。该离散化方法,对于候选部署点相对稀疏的外围部署区域,若某网格交点因所在位置的地形等环境条件限制其部署而被舍弃,但如果该点周围区域地理条件较好,则该点所在的大块区域缺少采样,降低了解的精度。针对此不足,本文提出将划分的小网格作为候选部署区域,同时在该区域内再次利用离散化思想根据地形、道路、水源、通信等条件优选出最适宜部署的地点,将该地点作为此区域的候选部署点,并记录该点相对要地中心的极角α和极径ρ,以此来确定该候选部署阵地的精确位置,若该网格的所有区域均不适宜部署,则不设置候选部署点。照此方法对所有网格区域优选候选部署点,如图2所示,所有这些点构成了防空武器的候选部署域,将所有防空武器按各自防线部署其中,随机组合形成部署方案集。改进后的方法既提高了候选部署阵地的质量,又提高了采样精度。从选择的候选部署点可以看出,距保卫目标较近的区域点较多较密,距保卫目标较远的区域点较稀疏,符合防空武器部署实际。
1.2 机动部署优化模型
敌对我要地空袭的作战方式为满载精确制导弹药的载机以要地为目标沿某方向来袭,到达投弹圈附近投射精确制导弹药后返航,投射的弹药在精确制导下以一定的速度飞向我方要地。只有在敌载机投射弹药前将其摧毁或将其投射的全部弹药摧毁才能成功保卫我方要地,部署的防空武器对我方要地的成功保卫概率,决定了部署方案的优劣。
根据防空武器杀伤区几何特点和火力单元的迎头射击规律,防空武器在空袭武器飞行高度的杀伤区截面近似为半圆形,且半圆直径垂直于来袭方向,半径为火力半径。如图3所示,当拦截目标沿θ角方向以Vh速度来袭时,经过某防空武器i杀伤区,该防空火力i相对要地的角度为αi,距离为ρi,火力半径为Ri,平均射击时间为tri,拦截目标在杀伤区的航迹长度为Li(θ),在该段被拦截了Ki(θ)次,每次拦截的毁伤概率为pi,该防空武器i对拦截目标的拦截概率为pi(θ),则
假设部署中程防空武器的数量为N1,近程防空武器的数量为N2,敌载机飞抵投弹圈附近投射n枚精确制导弹药。当空中目标以θ方向来袭时,我方防空武器系统成功保卫要地的概率为
可以看出,防空武器部署越靠近保卫要地,对空中目标的拦截次数越多,对目标拦截概率越大,防空武器将密集部署于要地周围。然而现实防空作战往往要求防空武器梯次配置层层阻击,加大火力纵深,因此,引入纵深部署系数S(θ)来描述θ方向上我方防空武器的梯次配置情况,取为θ方向上火力纵深,S(θ)越大则梯次配置效果越好。
实际作战中敌对保卫目标周围各方向的突袭概率往往是不相同的,存在主攻方向、次攻方向和其他方向等,为此将我方要地周围离散化为X个来袭方向,每个来袭方向的来袭概率为w(x)。根据防空部署重要方向重点部署其他方向适度部署和纵深梯次配置的原则,部署的防空武器系统整体防御效能Q由下式描述:
以上讨论了基于战场实时态势的防空部署方案对空防御效能,机动部署还应考虑机动过程中的约束。由于防空作战节奏快,机动防空武器必须在最大机动距离Jy约束下到达预定阵地,以迎接敌下一波次的空袭,Jy可根据历史作战数据或演习数据等确定。因此,机动防空武器装备从原各部署阵地机动到新的各部署阵地的平均移动距离须满足Jy约束。求机动防空武器装备从原各部署阵地机动到新的各部署阵地的最小平均移动距离,可抽象为图论中的最优匹配问题[8]。具有二分类(X,Y)赋权二分图G中的顶点部相当于各防空武器的原部署阵地,相当于各防空武器的新的部署阵地。任意两个阵地间的机动可根据路径长短、路况和安全性等因素规划出一条最优路径[9],任意边权重表示原阵地xi和新阵地yj之间的最优路径的长度,求平均移动距离最小的机动部署方案即转化为在赋权二分图G中寻找一个最小权值的完美匹配,可利用KM算法来求解。
因此,综合考虑机动后的部署防御效能和机动距离约束,得到防空机动部署优化的数学模型如下:
随着候选部署阵地的增多,会出现组合爆炸,可行解的数量急剧增多,需要借助智能优化算法求解。
2 优化求解
Memetic算法是一种将全局搜索算法和局部搜索算法组合起来的优化算法,具有良好的全局搜索能力,同时局部搜索可避免算法早熟,已广泛应用于各个工程领域且取得了满意的效果。本文采用遗传算法和邻域搜索算法组合的Memetic算法来求解优化模型。
2.1 编码方式
将解用二进制字符串表示,字符串的长度为候选部署点的数量,字符串的每一位对应一个候选部署点,该位为“1”表示部署了防空武器,为“0”表示未部署防空武器,故染色体中“1”的个数即为防空武器的数量。
2.2 适应度函数
本文的模型为约束优化问题,首先采用罚函数法将其转化为无约束优化问题,再以此目标函数作为适应度函数来评估解的适应度。
在此定义函数
适应度函数用下式描述
γ为惩罚系数,通过合理设计惩罚系数,有效引导搜索到可行解空间。
2.3 全局搜索操作
遗传算法具有全局搜索能力强,搜索不依靠梯度信息,对被优化目标的数学模型没有先验条件等特点,因此,利用遗传算法完成对最优解的全局搜索。遗传算法涉及到选择操作、交叉操作、变异操作等。
选择操作是在群体中选择生命力强的个体产生新的群体的过程。先按适应度大小对个体排序,然后按非线性规则来选择,使得适应度较高的个体被遗传到下一代群体中的概率较大。排序为r的个体被选择的概率为:
其中,q∈(0,1)为选择压力[10],由种群大小确定。采取最优保存策略,本代最优个体直接进入下一代。
交叉操作通过对两个染色体的交叉组合来产生新个体。由于染色体串中“1”的个数为定值,故在交叉操作时0和1须成对变化。首先随机配对得到双亲并按照交叉概率决定是否交叉重组。对于交叉重组的双亲,异或操作得到相异的基因位,对双亲中的一方任取0-1对交换,同时另一方相对应的基因位取反。
变异操作通过将个体染色体串中的某些基因位用其他等位基因来替换,从而形成新的个体。同理在变异操作时0和1须成对变化。变异时依据变异概率选取0-1对通过基因位的互换来完成变异操作。
2.4 局部搜索操作
局部搜索是基于贪婪思想在初始解x的邻域中搜索更好的解,若能找到则替换解x成为当前解,然后继续在其邻域搜索,重复此过程直到得到最终解[11-12]。本文对每代全局搜索得到的最优个体进行局部搜索操作,对最优个体的邻域进行深度搜索,考虑到算法的运行效率,在当前最优个体字符串中任选1个取值为“1”基因位,将其与取值为“0”的所有基因位分别作两两交换得到当前最优个体的邻域,来进行局部搜索操作。
3 仿真分析
本节将通过一个要地防空部署实例,来验证本文所提的机动部署优化模型在实际工程应用中的可行性和有效性。
我方保卫要地、周围待部署区域地形条件和据此提取的候选部署点,以及离散的初始敌各来袭方向突袭概率见图4,最外层的点为中程防空武器候选部署点,里层的点为近程防空武器候选部署点,敌空袭武器载机飞行速度为0.5 km/s,携带2枚智能弹药,智能弹药被投放后的飞行速度为0.2 km/s,我方待部署的防空武器型号数量性能见表1,该仿真实验假设所有防空武器均有较好的机动性能,机动调整部署中我方防空武器平均机动距离不超过30 km。战前部署不考虑机动距离因素,可利用式(6)的部署效能最大化来优化战前兵力部署,部署效果见下页图5。该部署方案在环境条件约束下在敌主攻方向上部署较多防空兵力且梯次配置,同时兼顾其他来袭方向进行了适当的兵力部署,最大化有限防空兵力的防御效能。
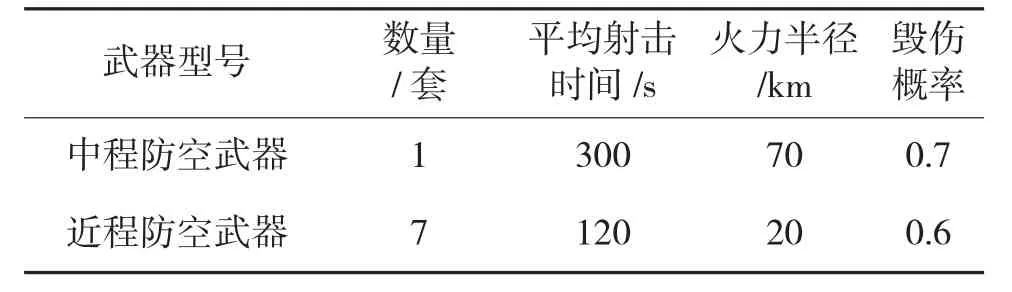
表1 防空武器数量性能表
随着防空作战的进行,敌主攻方向发生变化,且我方2部近程防空武器发生毁损,故需充分利用防空武器的机动性能开展战场机动调整部署以形成新的防御优势。若不考虑机动距离的约束,则利用式(6)优化求解得到的调整后的部署示意图,见图6。该部署在当前的战场态势下部署效能最优,但该机动部署方案平均机动距离为35.6 km,超出了限制。利用式(7)的数学模型进行优化求解,最后得出在满足机动距离约束条件下的最优部署方案如图7所示,该机动部署方案在重要方向部署了相对较多的兵力,且兼顾了其他方向,在机动距离的限制下最大化防御效能,与图5战前部署方案相比更适应当前战场态势,明显提高了防空武器整体防御效能,与图6相比虽然整体防御效能不及,但该机动部署考虑了机动距离因素,更符合防空作战实际。
4 结论
本文针对要地防空作战过程中兵力机动部署问题进行了研究,提出了一种基于Memetic算法的要地防空兵力机动部署优化算法。将各型防空武器按部署防线进行区分并运用离散化思想从各部署区域优选了若干候选部署阵地,将有限的防空兵力部署其中随机组合形成防空部署方案集,描述了基于战场实时态势的防空兵力部署方案防御效能评价方法,并结合防空作战机动调整部署的特点将机动距离作为约束,建立了防空兵力机动部署优化模型,并利用Memetic算法进行求解,最后利用要地防空机动部署实例进行了仿真分析,结果验证了所提模型和求解算法的合理性和有效性。区域防空中的兵力机动部署问题是下一步的主要研究内容。
