关于零模正则化逻辑回归问题的研究

吕佩雯

（华南理工大学，广东 广州 510640）

一、引言

设Rn是赋予了内积及诱导范数的有限维向量空间，考虑稀疏逻辑回归问题：令为样本，为类别标签，则逻辑回归模型为：

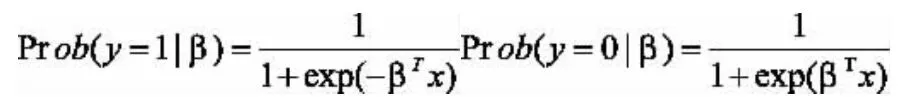
其中Prob(y=1/β)是在给定样本观测值β后，类别标签为l的条件概率，x为特征向量。

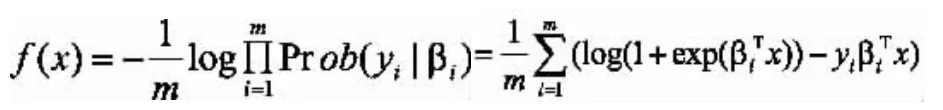
这是一个光滑的凸函数[1,3]，可以通过最小化逻辑损失的均值来求解特征向量x。

二、零模正则化

当训练集里的样本数m小于维数n时，直接求解容易出现过拟合，一般使用正则化来避免过拟合问题的出现。本文将使用零模正则，即求解零模正则极小化问题：

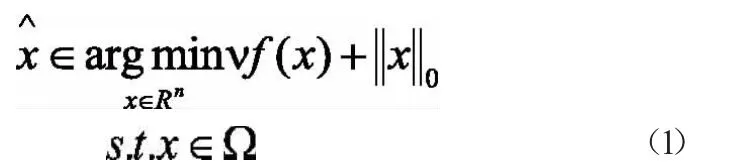
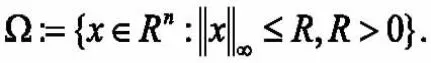
零模优化问题是一类带有组合性质的向量优化问题，（1）这种问题在计算上通常是NP难的，难以求得其全局最优解。而且，源于实际应用的零模优化问题通常具有较高的维数，根本不适合采用全局优化方法去寻求全局最优解。一个常用的处理方法是使用凸松弛技术,这种方法通过解一个或一系列易于处理的凸优化问题来产生一个理想的可行解或局部最优解。

三、零模正则化问题的等价模型

首先，从零模函数的变分刻画入手，可以得到零模正则问题的等价全局Lipschitz连续优化模型。对任意的，容易得到：

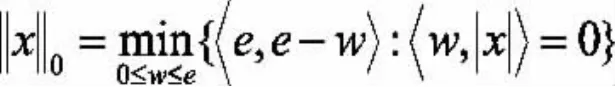
因此，问题的等价问题为：

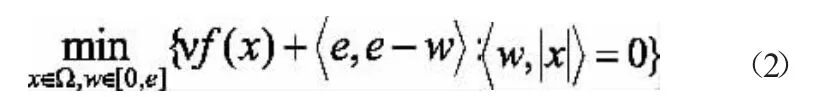
问题的可行集中包含着如下互补约束条件：

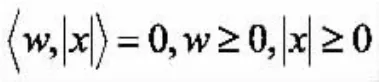
这说明零模正则化问题也是一个带有互补约束的数学规划问题(MPEC)。需要注意的是，MPEC在优化中也是一类很难的问题。虽然问题（2）的目标函数比原问题（1）简单，但却含有非凸互补约束，这比非凸目标函数更难处理。为解决这个非凸约束，考虑问题（2）的罚问题：

其中ρ＞0是罚参数。下面的定理1将说明问题（3）是问题（2）的全局精确罚，即他们有相同的全局最优解集[5]。在此之前，先建立定理证明需要用到的引理。

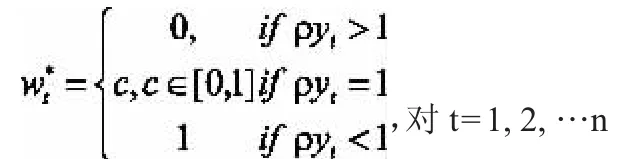
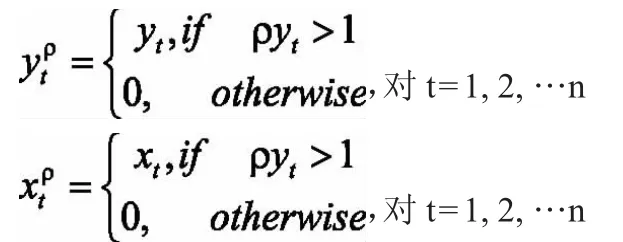
引理2.设函数f在集合上全局Lipschitz连续，若ρ＞VLf，则对任意的和，有：

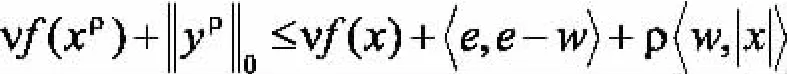
所以，只需证明：

由引理1，若wρ是下面问题的最优解则wρ的形式可以为对t=1,2,...n.所以，

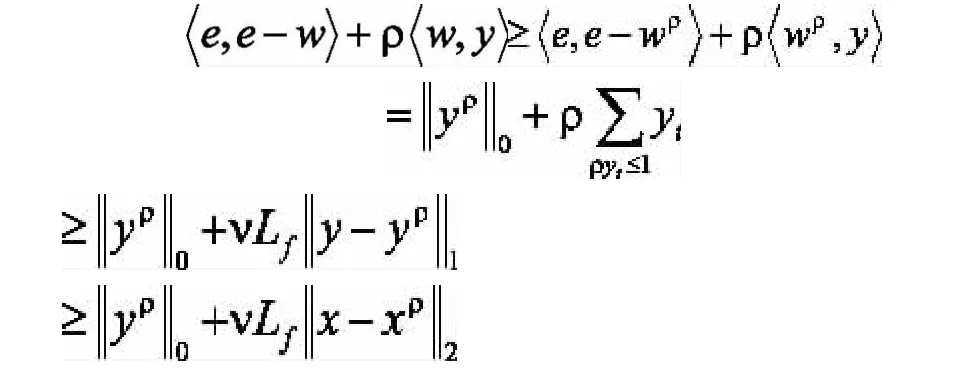
第一部分得证。下面证明第二部分：当等式成立时，

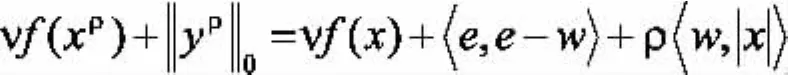
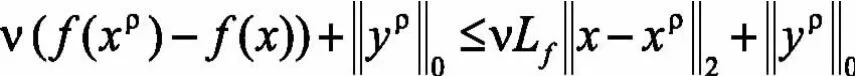
所以，

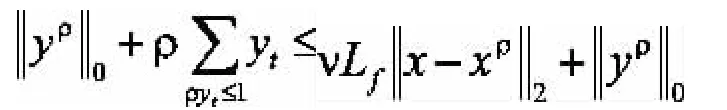
再加上ρ＞VLf，可得：

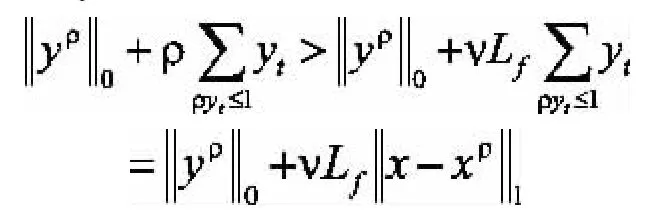
下面给出问题（3）是问题（2）的全局精确罚的理论保证：

证明.设问题（2）和问题（3）的可行集分别为 S 和 Sρ，问题（2）和问题（3）的全局最优解集分别为S*和S*ρ。令ρ＞vLf,首先证明：对任意的，有，且由引理2，

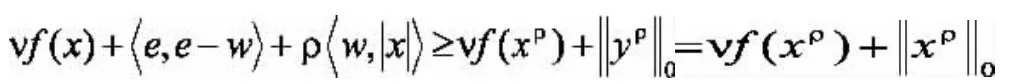
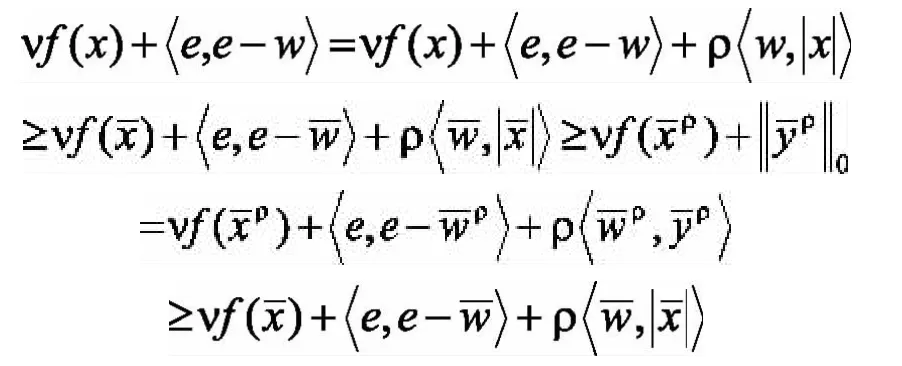
所以，

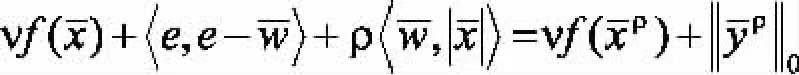
这样，求解问题（1）转化为求解罚问题（3）。虽然罚问题（3）非凸，但是这种结构使得它比零模正则化问题更好解决。当变量w选定时，f(x)为逻辑损失函数，罚问题（3）退化为关于x的凸的极小化问题；当变量x选定时，罚问题（3）退化为关于w的凸的极小化问题，这样的问题是有闭式解的。为此，针对f(x)为逻辑损失函数，将选用多阶段凸松弛法[4]来求解问题（3）。多阶段凸松弛法的主要步骤为：

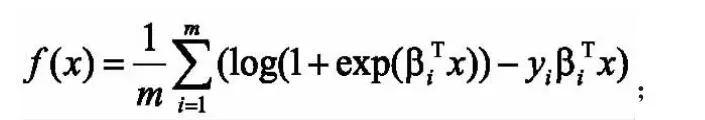
(S2)求解极小化问题：

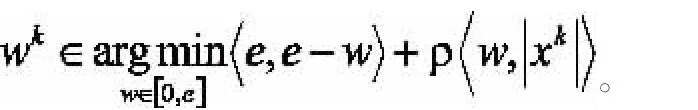
由引理1可知Wk是容易求得的，该方法的主要工作都在于解决一个加权的L1-正则化逻辑回归问题[6,9,10]。这是一类凸优化问题，所以它可以通过标准的凸优化方法求解，比如:增广拉格朗日法，内点法[7]，IRLS-LARS[8],路径跟踪法，迭代加权最小二乘法等。

四、结束语

本文借助零模函数的变分刻画，将零模正则化逻辑回归问题等价的写为带有互补约束的数学规划问题(简称MPEC问题)；然后证明将互补约束直接罚到目标函数上所诱导的罚问题是MPEC问题的全局精确罚(即与MPEC问题有相同的全局最优解集)。正如文中所说，此精确罚问题的目标函数不仅在可行集上全局Lipschitz连续，而且还具有满意的双线性结构，为设计零模正则化问题的多阶段凸松弛算法提供了满意的等价Lipschitz优化模型。