双排微型桩加固碎石土滑坡物理模型试验研究
2018-10-15胡时友李超杰
胡时友,蔡 强,李超杰
(1.成都理工大学环境与土木工程学院,四川 成都 610059;2.中国地质科学院探矿工艺研究所/中国地质调查局地质灾害防治技术中心,四川 成都 611734;3.成都航空职业技术学院,四川 成都 610100)
我国滑坡灾害频发,其中较为常见的一种滑坡类型是碎石土滑坡[1];而微型桩结构因布设灵活,适于在复杂狭窄的地质环境条件下快速施工且效果显著,被大量应用在滑坡灾害防治工程中,且取得了良好的效果[2~4]。目前,国内外学者已取得较多的微型桩研究成果。胡毅夫等[5]通过3组大型模型试验对比研究微型抗滑桩双排单桩与组合桩在加固边坡时的抗滑特性,结果表明桩体破坏有3种形式:桩体弯曲、桩土脱空、桩体断裂;双排单桩桩体自由段土压力沿桩身呈“S”型分布,桩前滑面层位存在桩土脱空区;后桩承受土压力大于前桩,土压力最大值在滑移面上10%桩长附近;组合桩加固效果更佳,较单桩抗滑力提高6.8%。朱宝龙等[6]通过离心模型试验研究了不同桩间距微型桩群的受力特征和桩身弯矩特征,研究结果表明桩间距的不同会影响各排桩之间的荷载分担比以及桩身最大弯矩出现的位置。陈强等[7]通过离心模型试验研究注浆钢管微型桩的受力特征,研究表明前桩所受的最大土压力约为后桩的13.3%,前桩的弯矩曲线由反S型逐渐变为S型,而后桩的弯矩曲线一直呈S型。苏媛媛等[8]通过对国内外研究结论的总结分析认为合理的桩间距能减小微型桩群由于群桩效应而产生的不利影响,但同时要兼顾微型桩与岩土体整体协调作用的发挥程度,以求获得最佳承载能力。周德培等[9]开展了顶板连接式微型桩组合结构抗滑机制的模型试验研究,在滑坡推力作用下,各排微型桩均能承担较大的弯矩,其中靠近滑坡后缘的排桩承担的弯矩最大,其余两排桩承担的弯矩相对较小。孙书伟等[10]开展框架微型桩结构抗滑特性的模型试验研究,结果表明框架微型桩结构中微型桩顶水平位移与荷载之间为双曲函数关系,且框架梁在荷载作用下发生倾斜,后排微型桩产生较为明显的被拔出趋势。闫金凯等[11]开展了微型桩与滑坡体共同作用的大型物理模型试验研究,微型桩各排桩在滑坡滑动时同时受力,且受力分布情况基本相同;各排桩同时发生破坏,破坏区域位于滑面上下各3倍桩径左右的范围内,为弯曲与剪切相结合的破坏模式。李志雨等[12]通过数值模拟研究了某滑坡治理工程实例,通过分析土拱效应的形成,得出距径比(桩间距/桩径)为5~8时土拱效应最理想。
以上研究成果大多分析了矩形分布的微型组合抗滑桩的受力变形特性,未涉及梅花形布设的微型组合抗滑桩的变形破坏特征。另外,由于岩土体复杂多变,也未考虑微型桩结构与岩土体间的相互作用对组合桩受力变形状态的影响。因此,本文通过开展梅花形布设的双排微型桩加固碎石土滑坡的物理模型试验,研究不同桩间距条件下各排桩的受力变形特征和滑坡推力传递规律,为微型桩的设计提供科学依据。
1 物理模型试验设计
1.1 试验目的和内容
利用模型试验槽,对双排微型桩加固碎石土滑坡的过程进行模型试验,重现其抗滑过程和特征。记录不同桩间距下双排微型桩桩顶位移、桩身应变和桩后土压力,分析微型桩群的受力变形特性。
1.2 模型试验相似条件
模型试验中,全部相似判据都满足的相似模型是极难获得的,只能使模型满足主要的相似判据。根据相似理论,凡是在几何相似条件下由动力学相似获得的解,理应满足运动学相似[1],即:
(1)
式中:λ——相似系数;
σ——应力;
γ——材料重度;
l——几何尺寸;
μ——泊松比;
ε——应变;
f——摩擦系数;
φ——摩擦角;
Ε——弹性模量;
C——黏聚力;
τ——抗剪强度。
在模型试验过程中几何相似比λl=1∶15,弹模相似比λE=1。
1.3 模型材料
(1)模型桩
模型桩由PVC管灌注水泥砂浆制成,其中,PVC管的截面尺寸为直径(d)20 mm,长0.55 m,水泥标号为325#,骨料采用的是粒径为1.0 mm的石英砂。
将模型桩简化为悬臂梁结构,在桩体顶端加集中荷载,通过多级加载进行模型桩的标定试验,根据弹性力学理论,得到模型桩的弹性模量E为0.04×104MPa。
(2)滑体材料
滑体土选择重晶石粉、石英砂、碎石颗粒和水进行配置,各种材料质量百分配比及试验材料的力学参数见表1~2。

表1 岩土体材料配比[13]Table 1 Mixture ratios of rock and soil materials

表2 试验材料力学参数Table 2 Mechanical parameters of the test material
(3)模型底面
模型底部用一层厚0.07 m的土层制作。由于滑体的滑动主要靠后部的加载装置推动,模型底面土体的力学参数对滑体滑动的影响很小,因而不考虑其强度对模型滑动的影响。
1.4 双排桩试验模型制作
试验共分3组,每组7根模型桩,桩间距Cd分别为4d、5d、6d,其中第一排有3根桩,第二排有4根桩,双排桩呈梅花型布设。模型桩底部采用角钢夹具将其固定在模型底面上部,模拟桩嵌固在基岩层内;滑体厚0.45 m,长1.75 m,微型桩长0.55 m,制备的模型见图1、2。
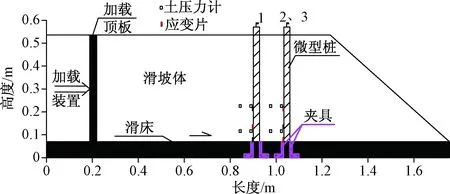
图1 试验模型剖面图Fig.1 Test model profile

图2 试验模型照片Fig.2 Test model photo
1.5 测试内容
考虑到试验模型完全对称及双排桩整体受力状态,并忽略掉边界效应的影响,取位于滑坡体中间位置的1#、2#、3#桩作为测试桩(1#桩位于第一排桩中线位置,2#、3#桩位于第二排桩临近中线位置的两侧,见图2),在测试桩位于滑面、滑面以上4 cm和9 cm处敷贴应变片以测试桩身力学状态,另在测试桩桩后位于滑面以上4 cm和15 cm处埋设土压力计以测试桩体承受滑坡推力的状态;此外,在测试桩顶设置位移控制点,监控加载过程中桩顶位移变化情况。
1.6 加载设计
滑坡发生滑动时,滑坡推力始终稳定作用在抗滑桩上,为模拟这个过程,在模型试验中用量程为20 kN的推力加载装置对模型桩后土体施加荷载,用以模拟微型桩所受到的滑坡推力,加载方式为分级加载,加载幅度为每次使滑体向滑坡前缘移动10 mm,滑体位移以S表示。在每级荷载施加后,均要持荷一定时间,至桩结构受力和变形趋于稳定后才施加下一级荷载。
2 试验结果分析
通过研究测试桩的桩顶位移、桩后土压力、桩身弯矩和滑坡推力传递系数分布情况,揭示不同桩间距下双排微型桩受力变形特性和滑坡推力传递规律。
2.1 桩顶位移分析
根据试验结果,建立不同桩间距下各排模型桩桩顶位移变化曲线,如图3所示。
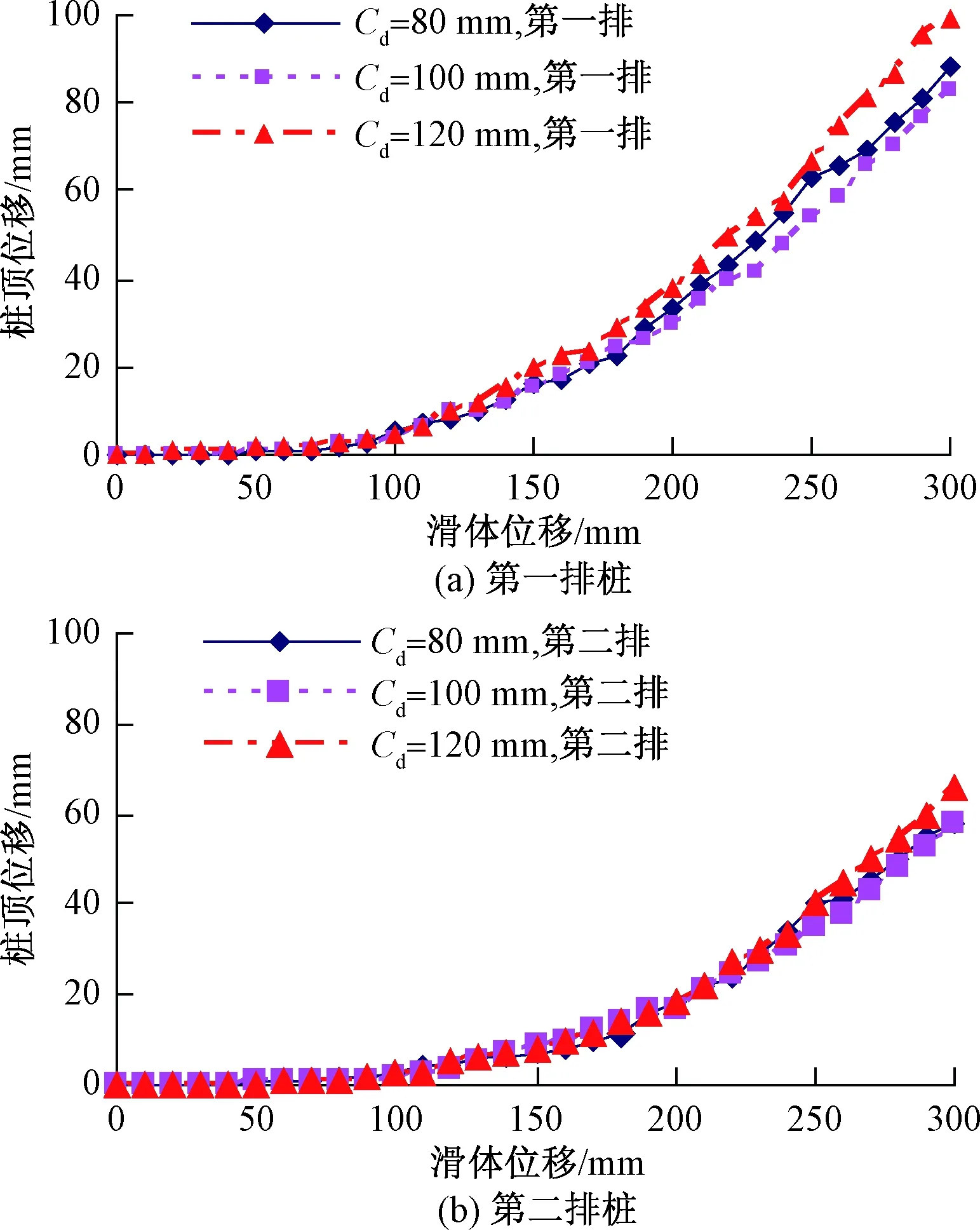
图3 桩顶位移变化曲线Fig.3 Displacement of pile top
加载开始后,由于土体产生瞬时变形,桩体上受到的推力较小,不足以使微型桩产生明显位移,此时第一排桩顶位移基本保持在2 mm以内,第二排桩顶位移保持在1 mm以内。当S>80 mm时,传递到微型群桩的推力逐渐增大,第一排桩顶位移才开始有明显的增长,微型桩进入弹性工作阶段。当S>160 mm时,排桩桩顶位移开始明显增长,随着水平推力的增长,第一排桩顶位移变化曲线出现突变点,曲线斜率陡然增大,微型桩处于弹塑性受力直至第一排桩失效。
当S>100 mm时,第二排桩顶位移才开始有明显的增长;当S>180 mm时,第二排桩顶位移增长幅度增大。
加载全过程中,桩间距为120 mm时,第一排桩桩顶位移增长最快,且增幅最大,表明微型群桩对桩间土的遮蔽阻挡效果越差,桩与土体共同作用的整体性越差;桩间距为100 mm时,第一排桩桩顶位移增长最慢,且增幅最小,表明此时桩土共同作用的整体性最好,桩身产生的角位移也最小。
同级水平推力作用下,不同桩间距下的第二排桩顶位移的变化规律与第一排桩基本上相同。
2.2 不同桩间距下桩后土压力分布规律
根据试验测试结果,不同滑体位移和桩间距下,滑面以上4,15 cm处的桩后土压力(滑坡推力)分布规律如图4所示。
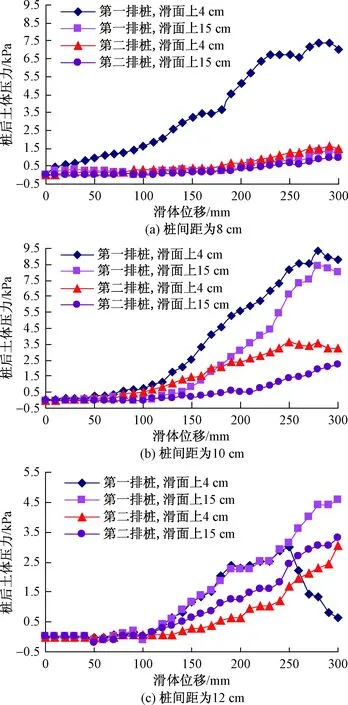
图4 持续滑动条件下桩后土压力分布曲线Fig.4 Curves of the pile soil pressure under the conditions of continuedslide
加载开始后,由于滑坡体后缘土体处于瞬时变形阶段,双排桩位于滑面上4 cm和15 cm处的土压力基本为0。随着滑体压缩变形持续增长,双排桩桩间土拱效应自上而下逐渐增强,通过土拱传递到第二排桩上的滑坡推力逐渐增大,且越靠近滑面处的滑坡推力增长越快。随后,桩间土拱被破坏,第一排桩进入弹塑性工作阶段,桩后土压力曲线出现突变点,土压力激增,很快第一排桩后土压力达到峰值,微型桩失效破坏,桩后土压力急剧减小,大部分的推力开始由第二排微型桩承受,第二排桩后土压力快速增长。
桩间距为80 mm时,当第一排桩滑面上4 cm处的土压力曲线出现第一个突变点后,第一排桩后土压力剧烈增加,曲线斜率变陡,第一排桩间土拱效应加剧,桩间土体传递到桩上的应力加大,但由于第一排桩与模型槽挡板间距过大,部分土体从桩外侧绕流,第一排桩后土压力出现波动。随着滑体的持续滑动,第一排桩间土拱达到其极限状态并被破坏,桩与桩后土体出现分离现象,桩后土压力出现波动,再次出现突变点,此时第一排微型桩进入塑性破坏阶段,达到极限抗滑状态。
桩间距为100 mm时,随着水平推力的加大,当S>140 mm后,第一排桩后土拱效应自上而下地逐渐增强,推力较好地传递到第一排桩上,位于滑面上4 cm和15 cm处桩后土压力变化曲线的斜率基本相同,这两个测点的土压力均呈现大幅度增长,但靠近滑面处的土压力增长较快,表明桩后土压力主要集中分布在滑面以上1/3桩身范围内,此时,传递到第二排桩的推力也逐步加大,桩后土压力明显增大。随着滑坡土体的持续滑动,第一排桩后土拱达到其极限强度,桩与桩后土体出现分离现象,微型桩进入塑性屈服阶段,第一排桩后两个测点的土压力均出现突变点并同时达到峰值,分别为8.37 kPa、9.35 kPa,随后第一排微型桩失效破坏,桩后土压力急剧减小,滑坡推力全部由第二排桩承担。
桩间距为120 mm时,当S≤100 mm,双排桩后土压力基本为0。随着滑体位移持续增加,第一排桩后土拱形成,桩后土压力增大,且第一排桩位于滑面以上1/3桩身范围内的土压力及其曲线斜率基本相同。当S=190 mm时,土压力曲线出现突变点,土压力增长幅度减缓,这是由于桩间距过大,桩后土拱强度较低,并且被破坏,桩后土体从桩间绕流,第一排桩与桩后土体出现脱空现象,第一排桩进入弹塑性受力阶段,此时传递到第二排桩后的推力加大,土压力快速增长。当S=250 mm时,第一排桩滑面上4 cm处的土压力到达峰值,随后急剧下降,说明第一排桩已被破坏,失去抗滑效果。第二排桩后土压力随着水平推力的增大而增大,且越靠近滑面上桩身1/3范围内的土压力越大。
2.3 不同桩间距下桩身弯矩分布规律
假设微型桩始终处于弹性工作阶段,根据标定试验测出的模型桩的弹性模量和沿桩身粘贴的应变片测出的应变值,由式(1)可计算出相应测点的弯矩值。
M=Wz·E·ε
(1)
其中:Wz——模型桩横截面抗弯系数;
E——模型桩的弹性模量;
ε——桩身应变值。
不同滑体位移和桩间距下,桩身的弯矩分布曲线如图5~7所示。
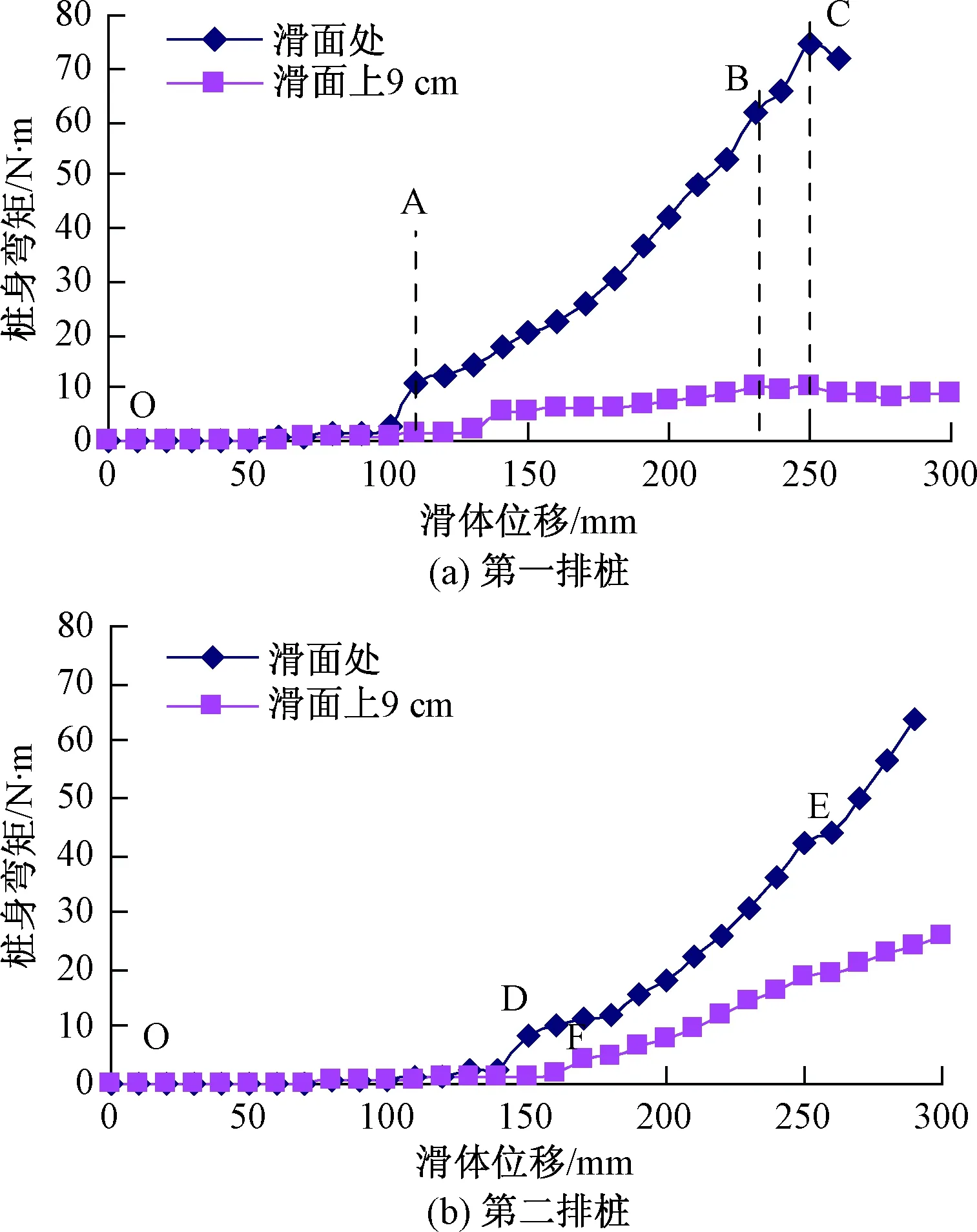
图5 桩间距为4d的桩身弯矩图Fig.5 Diagram of pile spacing of 4d bending moment
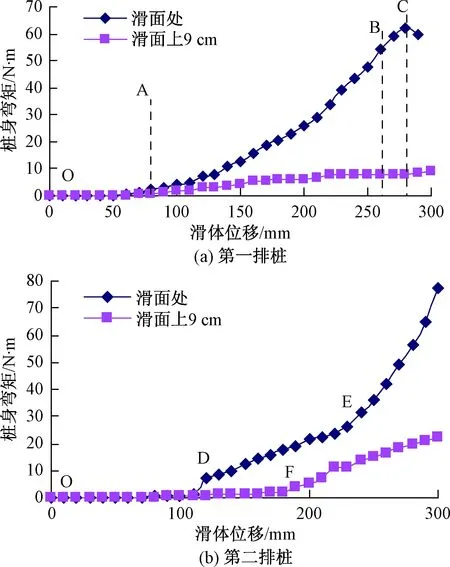
图6 桩间距为5d的桩身弯矩图Fig.6 Diagram of pile spacing of 5d bending moment
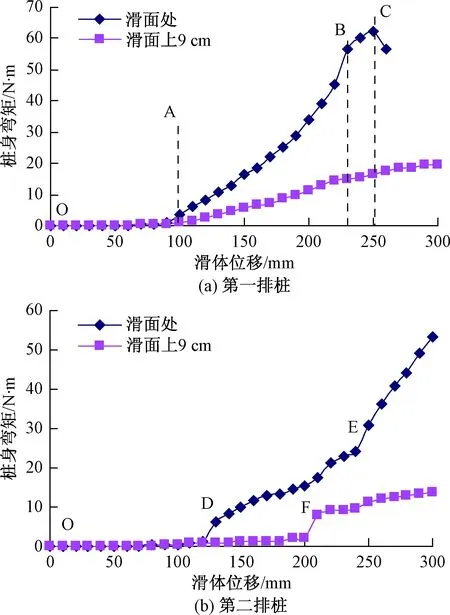
图7 桩间距为6d的桩身弯矩图Fig.7 Diagram of pile spacing of 6d bending moment
根据试验结果,加载开始后,一段时间内模型桩的弯矩基本为0(OA、OD段),双排微型桩基本没有产生位移,这是由于水平推力大部分用来克服桩后土体的阻滑力和挤压密实滑坡后缘土体,只有小部分的推力传递到第一排桩上,第二排桩没受到推力作用;随着滑体持续滑动,第一排桩后土拱形成,且强度由小到大,水平推力通过桩后土拱传递到第一排桩上增大,桩身弯矩快速增长,曲线斜率变大,通过桩排间土拱传递到第二排桩上的推力加大,第二排桩间土拱效应自上而下是逐步增强,桩身弯矩曲线出现第一个突变点D、F。当第一排桩身弯矩曲线出现突变点B,弯矩急剧加大,微型桩进入塑性工作阶段,弯矩很快达到其峰值C点,随后快速减小,第一排桩失效破坏。这个过程中(BC),第二排桩身弯矩曲线也出现突变点E,弯矩激增(EF),这是由于第一排桩刚产生塑性变形后,没有立即破坏,较大部分的推力逐渐传递到第二排桩上,当第一排桩超过其抗滑极限状态后,主要由第二排桩提供抗滑力。
双排微型桩从上到下,桩身弯矩由小到大,且滑面处的桩身弯矩较滑面上9 cm处大得多,表明该处的桩身弯矩是桩能承受的最大弯矩。
桩间距为4d时,随着滑体的持续滑动,当S=100 mm,第一排桩桩身弯矩曲线出现突变点B,表明桩后土拱形成,通过土拱传递到桩上的推力加大,第一排微型桩进入弹性工作阶段,推力开始传递到第二排桩上,当S=140 mm,第二排桩桩身弯矩曲线出现突变点D,桩排间的土拱形成。当S=230 mm时,第一排桩后土拱达到极限状态,第一排桩进入弹塑性受力阶段,很快达到其屈服极限,第一排桩桩身弯矩达到其能承受的最大抗滑弯矩74.36 N·m,这时,第二排桩桩身弯矩曲线出现第二个突变点E,随着第一排桩失效破坏,第二排桩承受的推力激增,桩身弯矩也剧烈增大。
桩间距为5d时,随着水平推力的增加,当S=70 mm,第一排桩桩身弯矩曲线出现突变点,桩后土拱形成,第一排桩开始承受推力。随着滑体的持续滑动,第一桩后土拱效应逐步增强,桩身弯矩大幅度增长。当S=110 mm,第二排桩桩身弯矩曲线出现突变点D,桩排间的土拱形成,当S=140 mm,出现第二个突变点E,桩前土体出现裂缝,而第一排桩仍处于弹性工作阶段,表明传递到第二排桩上的推力加大,双排桩开始共同提供抗滑弯矩,双排桩与桩间土形成一个整体,类似抗滑挡土墙。当S=260 mm,第一排桩桩身弯矩曲线出现突变点B,第一排桩进入弹塑性工作阶段,桩体内部产生少量细小的拉裂纹,桩体抗弯刚度减小,抗弯能力下降,很快达到其极限抗滑状态,出现弯矩峰值,为62.43 N·m,第一排桩开始退出抗滑状态,由第二排桩提供抗滑弯矩。
桩间距为6d时,随着滑体的持续滑动,当S=90 mm,第一排桩桩身弯矩曲线出现突变点B,表明桩后土拱形成,通过土拱传递到桩上的推力加大,第一排微型桩进入弹性工作阶段,推力开始传递到第二排桩上;当S=200 mm,第二排桩桩身弯矩曲线出现突变点D,桩排间土拱形成。当第一排桩达到其弹性受力极限时,第二排桩桩身弯矩曲线才出现第二个突变点E,表明双排桩开始共同承受推力。但很快第一排桩达到其能抵抗的最大抗滑弯矩62.09 N·m,随后第一排桩失效破坏,第二排桩承受的推力激增,桩身弯矩也剧烈增大。
2.4 滑坡推力传递系数分析
独立布置的双排微型桩抗滑模型试验,在不考虑桩排间和桩前土体抗力、滑动面摩阻力及边界效应的前提下,可以简化为两排相互独立的悬臂桩结构,那么,第一、二排桩受到的滑坡推力的比值应该与双排微型桩桩顶位移的比值一致。

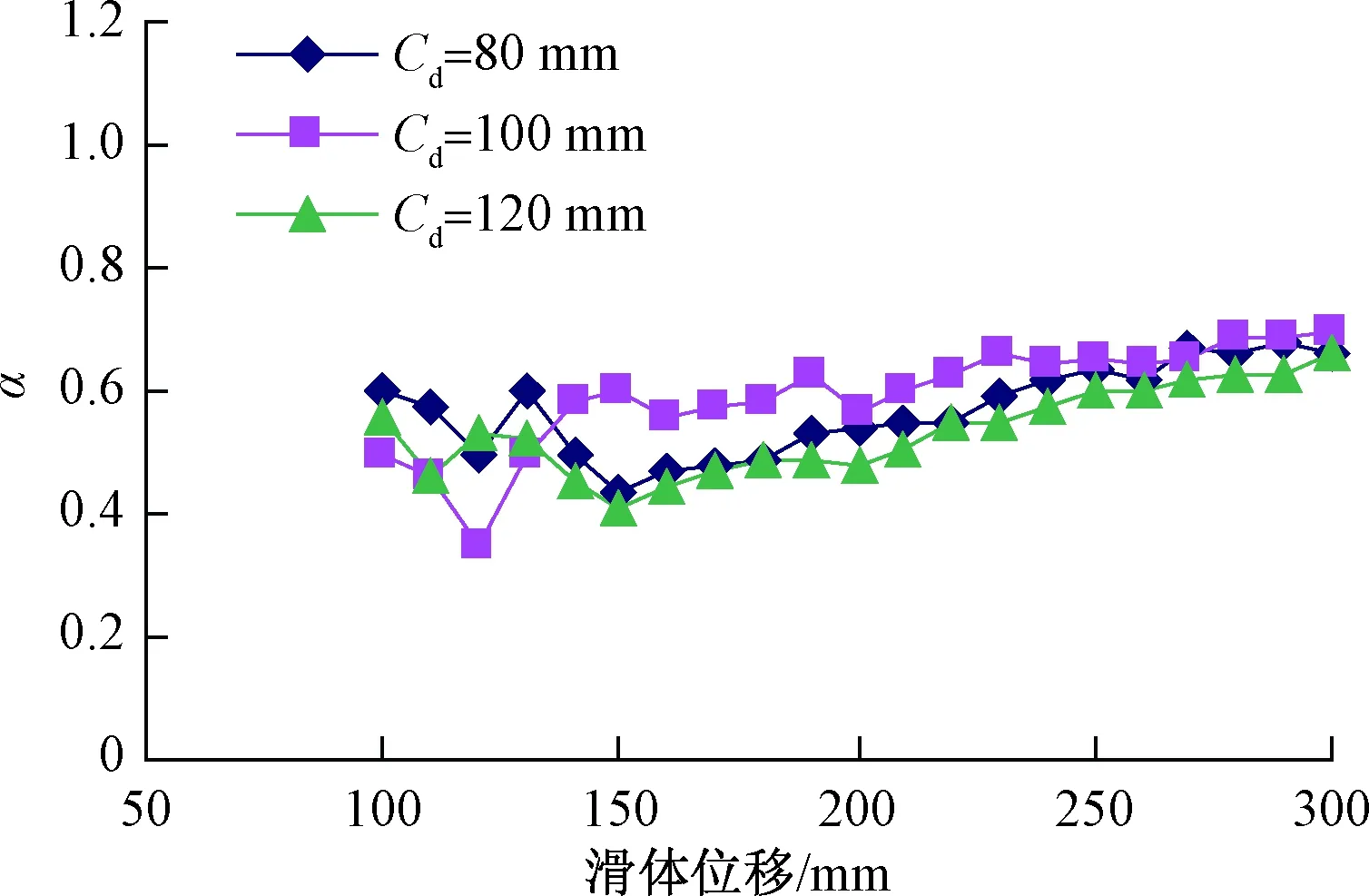
图8 滑坡推力传递系数分布曲线Fig.8 Curves of landslide thrust transmission coefficient
3 结论
通过对不同桩间距下双排微型桩加固碎石土滑坡的受力变形特性的研究,得到以下几点认识:
(1)在同等滑坡推力作用下,桩间距为5d时,微型桩群对桩间土的遮蔽阻挡效果最好,桩顶位移最小,桩间距4d时次之,桩间距6d时最大。
(2)双排微型桩承受的滑坡推力主要集中在滑面以上1/3桩身范围内,桩身最大弯矩位于滑面附近,且桩群均以第一排桩达到其弹性受力极限而失效。
(3)滑坡推力沿排桩呈逐渐减小趋势, 桩间距5d时,滑坡推力在排桩间分布较理想,排桩间滑坡推力传递系数α在(0.5,0.7)间取值。
