TBM隧洞衬砌渐变段局部水头损失研究

崔 润，焦景辉

(吉林省水利水电勘测设计研究院，吉林 长春 130021)

随着TBM掘进施工的普及，输水隧洞沿线地质情况复杂多变，支护型式。隧洞衬砌厚度沿线随其不同，相应的过水横截面尺寸亦发生变化，当水流经过洞径缩小或扩大段时，由于局部边界的改变，水流流态发生变化，产生涡流等现象，消耗更多的能量，此过程水流能量损失即为局部水头损失。

国内不少学者对管道的局部水头损失进行了专门的研究。Valiantzas[1]通过对比局部水头损失和沿程水头损失相互关系，对达西公式进行了修正。陈朝[2]通过CFD计算，研究分析管道不同体型变化对局部水头损失系数的影响，得出了不同体型的管道的局部水头损失系数随雷诺数的变化规律。李协生[3]对引水隧洞渐变段采用近似公式框算，并通过水工模型试验成果加以验证，确定对引水隧洞渐变段局部水头损失和沿程水头损失影响较大的因素。赵宝峰[4]等结合试验对管道突扩的局部水头损失系数进行了研究并对计算公式进行了修正；贺益英[5]等人通过水工试验分析管道中弯管局部水头损失与其他水力参数的关系，得到了不同弯管的局部水头损失系数；王开[6]等通过模型试验系统的研究了不同局部水头损失系数计算公式下计算结果不同的原因；陈姣姣[7]等采用数值模拟方法研究了水电站进水口渐变段水头损失与渐变段长度、隧洞长度和隧洞直径的关系，并通过量纲分析得到了其关系式。

研究表明：隧洞洞径变化引起的局部水头损失是必须要考虑的问题，其研究成果对工程的计算设计有很强的指导意义，不同工程由于其结构参数和水力参数的不同，研究总结的局部水头损失系数也不尽相同，因此针对某一具体工程，需要研究确定局部水头损失系数。

本文采用数值模拟方法对隧洞洞径收缩段的局部水头损失系数的变化规律进行了研究，分析了不同收缩段角度、不同洞径对局部水头损失系数的影响。

1 数值模拟

1.1 控制方程

连续方程：

(1)

动量方程：

(2)

k方程：

(3)

ω方程：

(4)

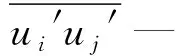
1.2 数值求解方法

有限体积法具有较高的计算效率，本次计算采用有限体积法进行离散；速度压力耦合校正采用SIMPLEC算法，其优势为收敛速度快；为保证计算精度，收敛标准残差控制在0.0001[9]。

1.3 计算边界条件

计算各工况采用统一的边界条件：进口边界设定为压力进口，压力取4×105Pa；出口边界设定为速度出口，出口速度取1m/s；固体边界条件采用无滑移条件，粗糙度Δ取值为0.3mm。

1.4 计算区域及网格的划分

计算区域包括上游段、洞径渐变段及下游段，模拟上游段长度70m，下游段70m，计算范围如图1所示。

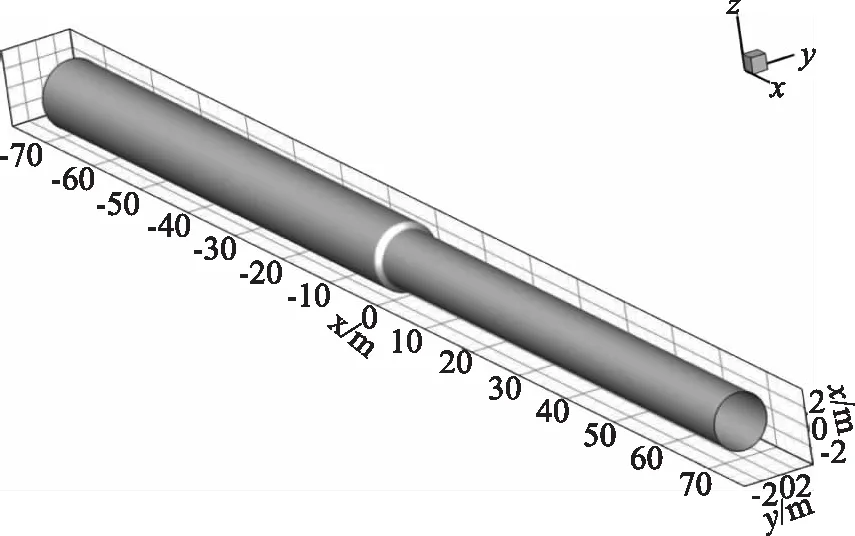
图1 模拟计算区域

计算区域的网格划分采用六面体分区，能够减少网格的总体数量，提高计算效率；计算区域划分为3段，避免出现楔形网格，提高计算的准确性；边壁附近网格加密，模拟近壁面的黏性层，可提高计算精度。如图2所示，计算区域网格总数约为52万。

图2 局部计算网格图

1.5 数值模拟工况

图3是隧洞变径纵断面示意图，上游洞径D1，下游洞径D2，渐变段水平长度为l，渐变段边壁夹角为θ，为研究不同工况下隧洞洞径收缩对局部水头损失系数的影响，取D1/D2=1.1、1.3和1.5，θ=20°、60°和90°。

2 数值模拟结果与讨论

2.1 渐变段边壁夹角θ对水头损失的影响

水流经过隧洞渐变段时，流线发生偏折，水流相互碰撞消耗更多能量，不同的偏折角度，水流碰撞的激烈程度不同，渐变段边壁夹角θ是水头损失的重要影响因素，数值模拟中固定上下游断面尺寸，取D1=7.07m，D1/D2=1.2，研究不同渐变段边壁夹角θ=20°、60°和90°对水头损失的影响。

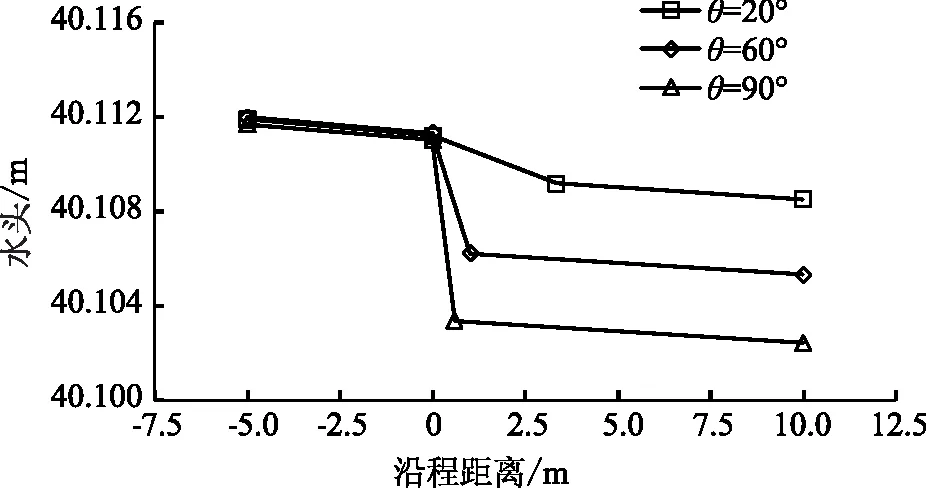
图4 水头经过渐变段沿程变化

图4为不同渐变段边壁夹角θ下隧洞内水头沿程变化，可以看出由于隧洞边壁具有一定糙率，洞内水头沿程略有减小，经过收缩段时，产生局部水头损失，洞内水头下降明显，通过收缩段后，水头下降趋于平缓；随着渐变段边壁夹角θ增大，洞内水头下降越显著，即局部水头损失增大；不同θ收缩段后的平顺段，3条水头线基本平行，沿程水头损失无变化。

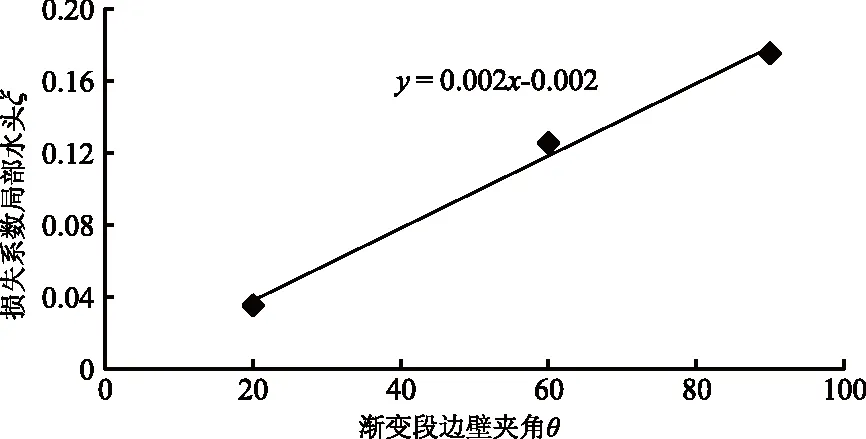
图5 局部水头损失系数ξ随边壁夹角θ的变化

图5为局部水头损失系数ξ随边壁夹角θ的变化，可以看出，局部水头损失系数ξ与渐变段边壁夹角θ具有良好的线性关系，以斜率k=0.002的比例关系变化，渐变段边壁夹角θ直接影响着局部水头损失系数ξ。由图5可得表1不同的边壁夹角θ对应局部水头损失系数ξ。

表1 局部水头损失系数ξ

2.2 渐变段边壁夹角θ对水头损失的影响

水流经过隧洞渐变段时，在相同的偏折角度下，不同洞径收缩比，水流碰撞的激烈程度不同，渐变段边壁夹角θ是水头损失的重要影响因素，数值模拟中固定上游断面尺寸D1=7.07m，渐变段边壁夹角θ=20°，研究不同洞径收缩比D1/D2=1.1、1.2和1.3对水头损失的影响。

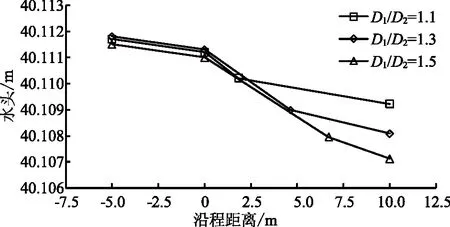
图6 水头经过渐变段沿程变化

图6为不同洞径收缩比D1/D2=1.1、1.3和1.5下隧洞内水头沿程变化，可以看出由于隧洞边壁具有一定糙率，洞内水头沿程略有减小，经过收缩段时，产生局部水头损失，洞内水头下降明显，通过收缩段后，水头下降趋于平缓；随着洞径收缩比增大，3种工况下水头减少斜率大致相同，由于收缩段长度逐渐增加，总水头损失逐渐增大；3种工况下收缩段后的平顺段，3条水头线下降趋势随收缩比加大而加大。

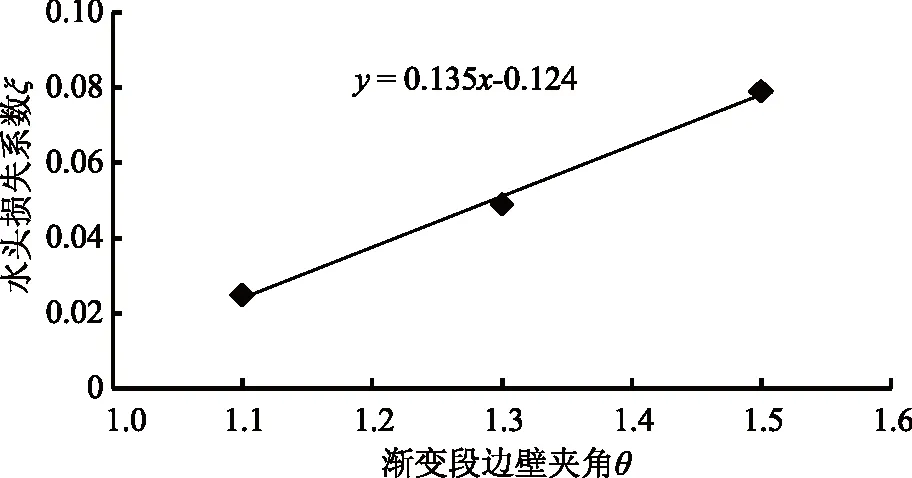
图7 局部水头损失系数ξ随洞径收缩比D1/D2的变化

图7为局部水头损失系数ξ随洞径收缩比D1/D2的变化，可以看出，局部水头损失系数ξ与洞径收缩比D1/D2具有良好的线性关系，以斜率k=0.13的比例关系变化，渐变段洞径收缩比D1/D2直接影响着局部水头损失系数ξ。由图7可得表2不同的洞径收缩比D1/D2对应局部水头损失系数ξ。

表2 局部水头损失系数ξ

3 结语

本文通过CFD对隧洞洞径收缩段水流进行数值模拟，研究了不同收缩段角度、不同洞径对局部水头损失系数的影响。得到了以下结论：

(1)在D1=7.07m，D1/D2=1.2时，随着渐变段边壁夹角θ增大，洞内水头下降越显著，局部水头损失系数增大，θ=10°、20°、40°、60°、90°时，局部水头损失系数相应为0.018、0.038、0.078、0.118、0.178。

(2)在D1=7.07m，渐变段边壁夹角θ=20°时，随着洞径收缩比D1/D2增大，洞内水头下降越显著，局部水头损失系数增大，经过收缩段后，3条水头线下降趋势随收缩比加大而加大。D1/D2=1.1、1.2、1.3、1.4、1.5时，局部水头损失系数相应为0.0245、0.038、0.0515、0.065、0.0785。

(3)本工程D1=7.07m，D1/D2=1.09，θ=5.3°，插值计算局部水头损失系数ξ=0.0063，局部水头损失hm=3.2×10-4m，水头损失较小，该渐变段设计较合理。