导流叶片数量及排布方式对涡流工具性能的影响

2018-10-15廖锐全赵亚睿程福山

西安石油大学学报（自然科学版） 2018年5期

张昭，廖锐全，赵亚睿，程福山，刘捷

(1.长江大学石油工程学院，湖北武汉 430100； 2.中国石油天然气集团公司气举试验基地多相流研究室，湖北武汉 430100；3.长庆油田第十一采油厂，甘肃庆阳 745000； 4.新疆油田工程技术研究院，新疆克拉玛依 834000)

引言

螺旋流因其具有能量集中、携带能力强的特点，在工业方面有着广泛的应用，如旋风分离器、水力旋流器、气力输送、强化传热等。近年来，螺旋流在石油行业中的应用也日益受到重视，石油工作者们相继进行了许多积极的探索和尝试，主要包括套管旋流扶正器[1]、油水分离用水力旋流器[2]、井下涡流工具[3]和聚驱采出井杆管防偏磨[4]等，均取得了较好的应用效果。其中，井下涡流工具(下称涡流工具)是一种新型的井底积液助排工具，可用于低压低产气井排除井底积液，提高气井生产效率。室内实验[5-6]和现场应用[3,7]均表明，该工具可以有效地降低气井临界携液流速，减少流动压降损失，提高气井的携液能力。目前，涡流排水采气技术在国外已成功推广应用，但在我国仍然处于现场试验阶段，如大庆徐深气田、长庆苏里格气田、四川蜀南气矿、吉林油田和新疆油田等。

常规的井下涡流工具如图1所示，主要由打捞头、绕流器、导流筒和坐封器组成，其中绕流器是主导流体流动的核心部件，由1个实心轴和固定在其表面的螺旋导流叶片组成。相比其他传统的排水采气工艺，该工具结构简单，无运动部件，而且不需要额外的能量补充。

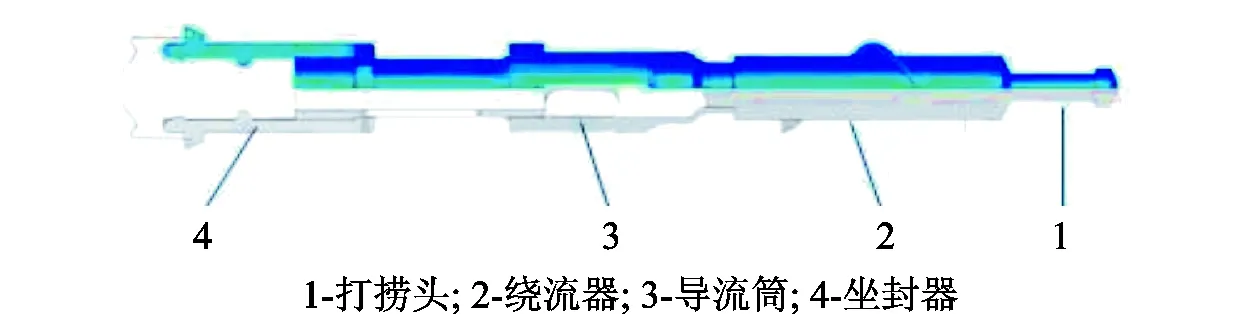
图1 涡流工具结构Fig.1 Structural diagram of downhole vortex tool

目前，对涡流工具的研究主要集中在单叶片结构参数优化上[8-11]，而关于导流叶片数量和排布方式对涡流工具性能的影响鲜有报道。然而许多研究均表明，叶片数量及排布方式对叶轮机械的工作性能具有重要影响。Liu等[12]人采用数值模拟和室内实验相结合的方法，研究了叶片数量对离心泵内部流场和空化性能的影响。结果表明增加叶片数量会增加离心泵的压头，减少离心泵中“喷射”和“尾流”的混合损失，而叶片数量对泵的效率和净正吸入压头影响较为复杂。2011年，Singh等[13]人研究了导流叶片数量和叶片高度对低水头轴流式涡轮机性能的影响，发现相比叶片高度而言，导叶数量对其性能的影响更大，而且随着叶片数量的增加，涡轮机工作效率呈降低趋势，增加叶片数量虽然增大了流体轴向流速，但同时也降低了流体的切向速度。龚斌等[14]采用数值模拟的方法研究了不同扭旋叶片组合对静态混合器流场特性的影响，研究发现一个截面上叶片数量越多，径向混合效果越好，对流体湍动的强化程度越大，流体阻力也越大。王鲁平等[15]研究了导流叶片叶形与数量对轴流式旋风除尘器性能的影响，结果表明随着叶片数量的增加，叶片出口截面的平均切向速度、局部压力损失和全局压力损失均增大。从以上研究中可以看出，叶片数量及排布方式对叶轮机械性能影响较为复杂，而且不同结构间差异性显著。因此有必要开展导叶数量及叶片排布方式对涡流工具性能的影响。

涡流工具性能可通过下游螺旋流的流动特性来反映，主要包括螺旋流内部的流速分布、压降特性以及螺旋流衰减特性[16]。因此，本文拟采用数值模拟和理论分析相结合的方法，在叶片数量不超过12的条件下，研究导流叶片数量及排列方式对气液两相螺旋流流动特性的影响，从而为涡流工具的设计和结构改进提供理论依据。

1 数值计算模型与方法

1.1 物理模型及网格划分

针对图1所示的涡流工具，本文以绕流器为研究对象，建立了如图2所示的简化模型。该模型由油管段和置于油管段中的绕流器组成，其中绕流器芯轴直径42 mm，导流叶片宽度6 mm，叶片螺旋角54°，叶片轴向长度118.7 mm，导流叶片外缘与油管壁紧密贴合。计算域坐标原点在工具出口截面中心处，流体流动方向沿z轴正方向，重力加速度沿z轴负方向。

图2 物理模型Fig.2 Physical model

根据叶片的空间位置关系，本文将导流叶片排布方式分为两种(图3)，环形排列和连续排列。所谓环形排列是指多个叶片均匀地分布在同一截面(圆周)上；而连续排列是指相邻叶片间首尾相接，沿螺旋线形排列。在保证芯轴直径、叶片宽度和螺旋角不变的情况下，对以下十种类型涡流工具(表1)展开了研究。

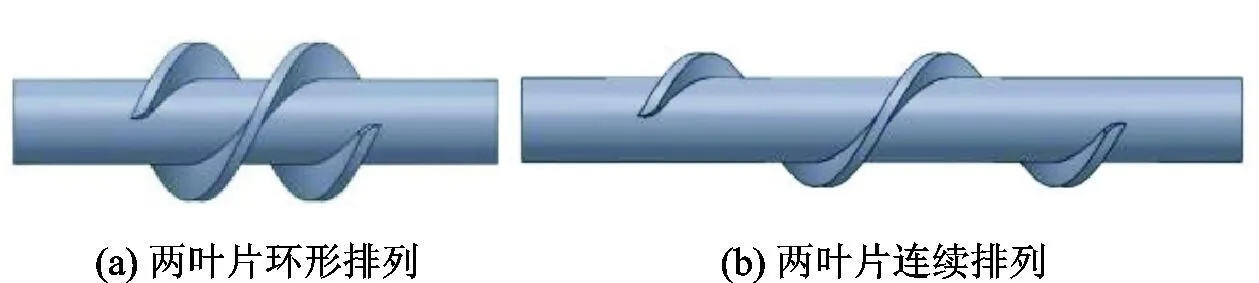
图3 导流叶片排布方式Fig.3 Arrangement patterns of guide vanes

排列方式导流叶片数量/个环形排列24681012连续排列1234

对数值计算而言，高质量的网格对提高计算精度、收敛性和稳定性具有重要意义。本文研究过程中计算模型均采用六面体结构化网格，而且为了捕获管壁附近的流动特征，对油管壁和螺旋导流板表面附近的网格进行了加密处理。图4为单叶片涡流工具计算域网格。

图4 单叶片计算域网格Fig.4 Grid division of calculation domain for single blade

1.2 数值模型

气液两相流体流过涡流工具后，由于离心力的作用，密度较大的液相会逐渐向管壁聚集形成液膜，气相则分布于管道中心。因此本文采用充分考虑流体界面特性的欧拉模型，对每一相分别建立动量方程和连续性方程。假设流体在含涡流工具圆管中的流动为稳态、三维不可压缩等温流动，则控制方程可描述为[17]：

连续性方程

▽·(αqρquq)=0；

(4)

动量方程

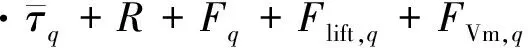
(5)

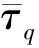
许多研究[18-20]表明RSM模型能够捕捉近壁区域应力的各向异性，相比其它涡黏模型，该模型可以更好地预测螺旋流的特征。因此本文采用RSM模型来模拟涡流工具产生的气液两相湍流运动。

1.3 边界条件及求解控制

本文采用Fluent软件进行数值计算，模型入口采用速度入口边界，模拟介质为水和空气，水的密度为998.2 kg/m3，空气的密度为1.225 kg/m3，指定各相的入口流速为2.5 m/s，水的体积分数为0.01，入口湍流强度采用经验公式I=0.16Re-1/8计算[21]；模型出口按充分发展管流条件处理，采用outflow出口边界。由于涡流工具无运动部件，因此壁面边界速度无滑移，壁面边界层用标准壁面函数处理。压力-速度耦合采用SIMPLE算法，动量、湍动能、湍流耗散率方程和雷诺应力方程均采用二阶迎风插值格式。

1.4 网格无关性检验及模型验证

为了确定足以捕捉流场流动特征的最合适的网格数量，进行了网格无关性检验。图5显示了单叶片模型在不同网格数量下出口截面气相的轴向速度和切向速度剖面，从图中可以看出网格2、网格3和网格4的计算结果非常接近，说明当网格数量达到1 328 760时，增加网格数量对计算结果影响不大。因此，确定无关性网格数量为1 328 760。

图6显示了有无涡流工具条件下计算管段的沿程平均压降分布。从图中可以看出流体流过涡流工具段时会产生较大的局部压降，而出涡流工具后由于芯轴的突然消失产生圆柱尾流，对流动产生扰动，导致压降降低(z=0～250 mm)；之后随着流动趋于稳定，压降呈近线性增加(z=250～600 mm)。对比有无涡流工具条件下稳定段的压力梯度，可以发现在涡流工具作用下稳定段的压力梯度(G1=0.068 5 Pa/ mm)比无涡流工具时(G2=0.114 9 Pa/ mm)要低。这与Ali等[5]人的实验结果是一致的，说明本文模拟结果能够合理地反映实际流场中压降的变化。

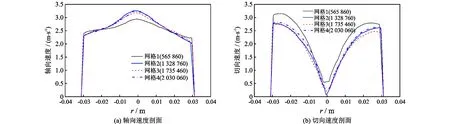
图5 不同网格数量下模型出口气体轴向速度和切向速度剖面对比(Z=600 mm)Fig.5 Axial and tangential velocity profiles of gas at outlet under different grid number (Z=600 mm)

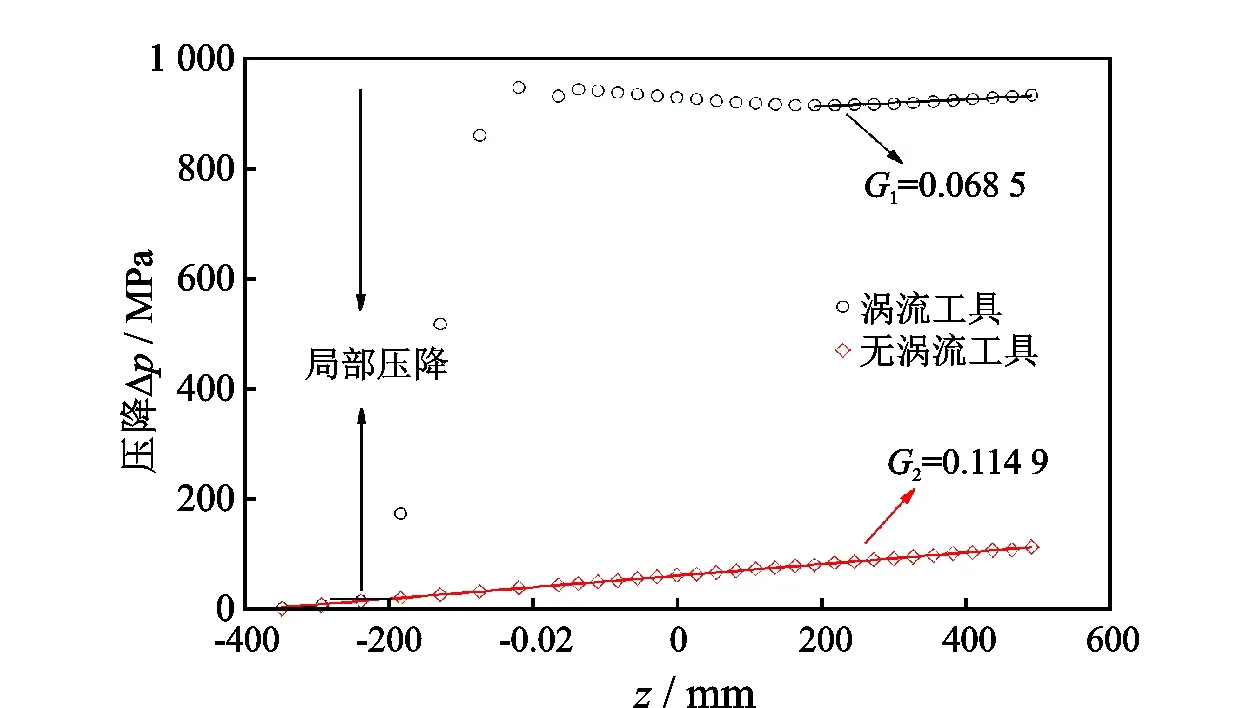
图6 有无涡流工具条件下沿程平均压降分布对比Fig.6 Comparison of average pressure drop distribution along the pipe section with and without downhole vortex tool

2 结果分析与讨论

2.1 流场分析

涡流工具下游液相分布如图7所示。从图中可以看出，流体经过涡流工具后，由于离心力的作用，密度较大的液相逐渐向管壁聚集形成液膜，而密度较小的气相则主要分布在流场中心形成气芯。显然，涡流工具的存在改变了流体的流动型态，而且随着流动的发展，周向液膜趋向均匀分布，液膜厚度由于液滴的沉积逐渐增大。

图7 不同导叶数及排列方式下液相分布Fig.7 Distribution of liquid volume fraction under different guide vane number and arrangement patterns

此外，通过对比可以发现，环形排列方式(m=2～12)下，导流叶片数量的增加对液相分布的影响不是很明显；而连续排列(n=1～4)时，增加叶片数量会导致管壁处的液相略有增加(如n=4)，这是因为连续排列下叶片数越多，涡流工具段越长，流体在工具段旋转作用时间也更长，更多的液滴在离心力作用下在壁面沉积。

与垂直轴流相比，螺旋流最大的区别在于具有一个与轴向速度相当量级的切向速度，其大小和分布对旋流的流动特性有决定性影响[22]。图8和图9分别反映了不同导叶数及排列方式下工具下游气相轴向速度和切向速度分布。从轴向速度云图可以看出，流场中轴向速度既有正值也有负值，负值出现在近涡流工具出口端(Z=0 mm)流场中心，说明流体出涡流工具后中心区域存在回流，轴向速度高速区位于管壁附近。Rocha(2015)[23]认为这是由于涡的破碎引起的。这种现象随着流动的发展会逐渐消失，高速区逐渐向管道中心转移(Z=600 mm)。从图8中还可以看出，轴向速度分布与导流叶片数量和排列方式有关。环形排列方式下，导叶数越多，回流越严重，旋流发展段越长，连续排列时则正好相反。

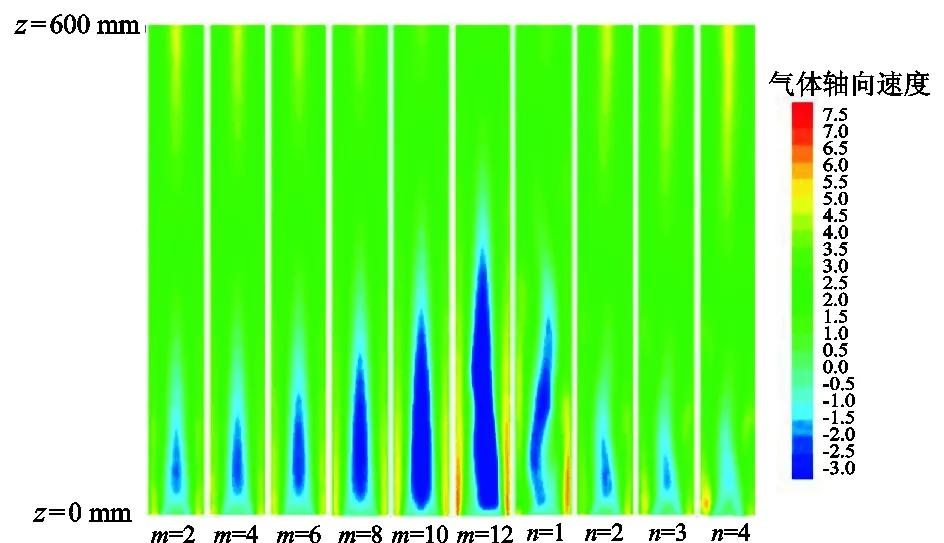
图8 轴向速度分布云图Fig.8 Distribution of axial velocity

从切向速度云图(图9)可以看出，流体切向速度在近涡流工具出口端(Z=0 mm)最大，并且沿轴向方向由于管壁的摩擦而逐渐衰减。径向上，切向速度呈近对称分布，结合图5(b)可以发现，气体切向速度在流场中心处近似为0，而后随着径向坐标的增大快速递增，增至最大值后在壁面附近又迅速降为0。可见气体的旋转动量主要集中在管壁附近，这有利于液膜的携带。此外，不同导叶数量和排列方式下气体切向速度分布也不同。通过对比沿程气体平均切向速度(图10)可以看出，环形排列时，气体平均切向速度随导叶数的增加而增大，而连续排列时正好相反；相同导叶数条件下，环形排列时测试段的平均切向速度普遍大于连续排列，这是因为连续排列时导流叶片轴向长度更长，产生的摩阻损失更大。

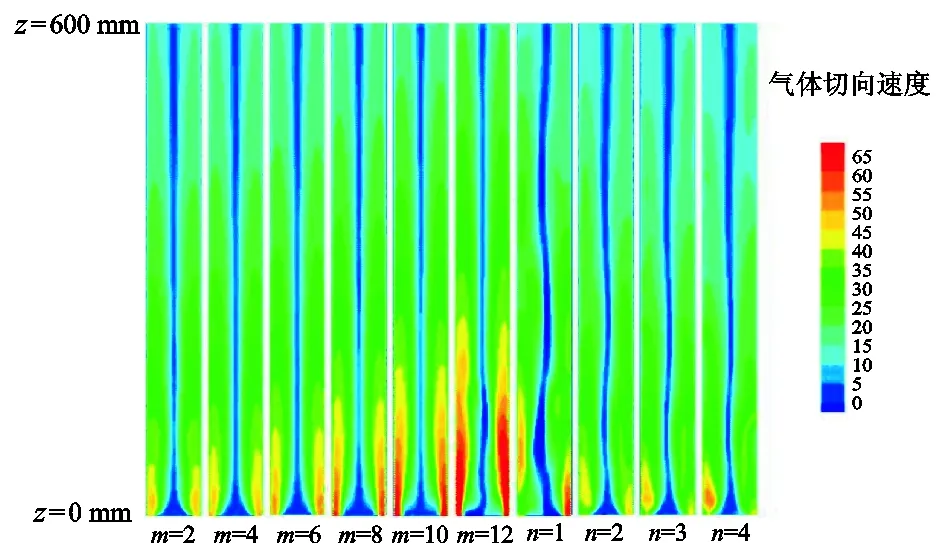
图9 切向速度分布云图Fig.9 Distribution of tangential velocity

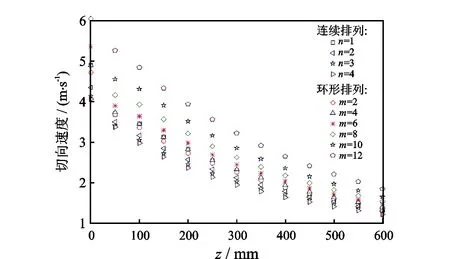
图10 不同排列方式下沿程平均切向速度分布Fig.10 Distribution of average tangential velocity along the pipe under different guide vane arrangement patterns

2.2 导叶数量及排列方式对压降的影响

表2显示了不同排列方式下导流叶片数量对涡流工具局部压降(Δpj)和管段总压降(Δpt)的影响，从表中可以看出，无论是环形排列还是连续排列，涡流工具产生的局部压降和管段总压降均随导流叶片数量的增加而增大；并且在环形排列方式下，导叶数越多，局部压降增加幅度越大，而连续排列时局部压降随导叶数增加线性递增(图11)。此外，当叶片数量相同时，环形排列方式下的局部压降和总压降均要小于连续排列方式。

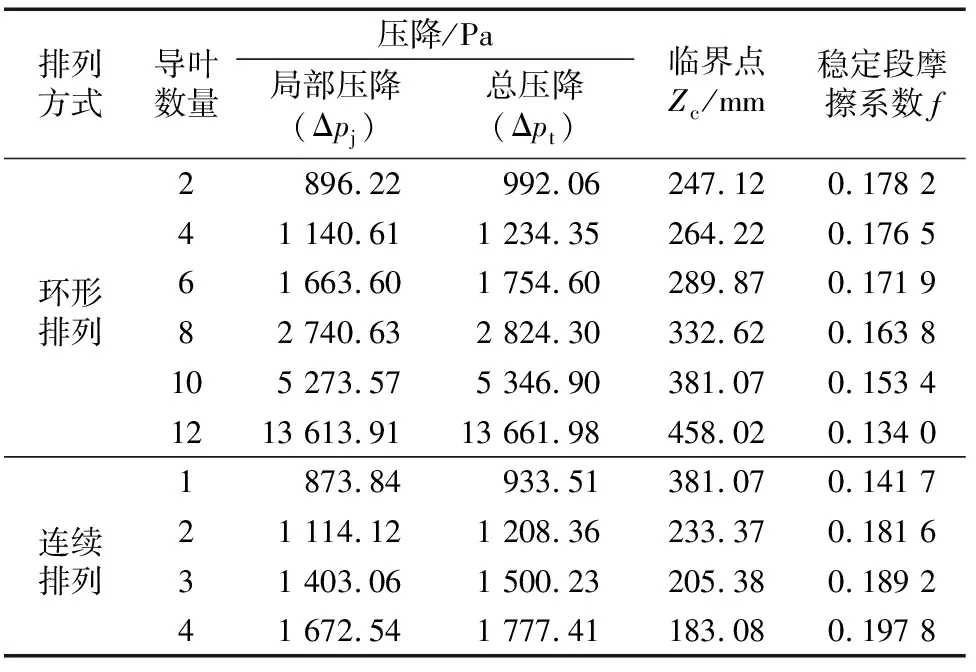
表2 不同排列方式和导流叶片数量下管段压降及摩擦系数Tab.2 Pressure drop and friction factor under different guide vane number and arrangement patterns

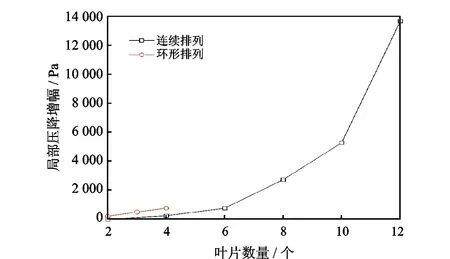
图11 导流叶片数量对局部压降增幅的影响Fig.11 Effect of guide vane number on local pressure drop increase

在真实气井中，涡流工具产生的局部压降相比井筒总压降很小，可忽略不计，人们更为关注的是涡流工具下游段井筒压力梯度。图12中，涡流工具下游测试段可根据流体压降的变化趋势分为旋流发展段和稳定段，图中G为稳定段压力梯度。在发展段压降呈先增后减的趋势，压降增大是由于流体出涡流工具时流动截面突增所致，而后压降递减是因为涡的破碎导致中心区域流体回流所致；在稳定段流体压降近似呈线性递增。不同导叶数量和排列方式下，旋流发展段向稳定段转变的临界位置(Zc)如表2所示。

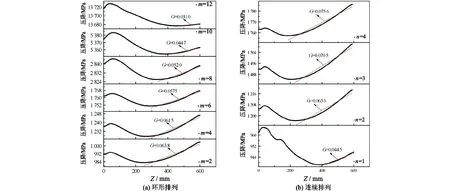
图12 不同导流叶片数量和排列方式下管段压降对比Fig.12 Average pressure drop distributions along the pipe section under different guide vane number and arrangement patterns

对比稳定段压力梯度可知，环形排列方式下，导流叶片数量越多，压力梯度越小，导叶数从2增至12时，压力梯度从0.063 8 Pa/mm降至0.031 0 Pa/mm；而连续排列时，随着导流叶片数量的增加，涡流工具下游稳定段的压力梯度呈递增趋势，且均高于相同数量叶片在环形排列方式下的压力梯度。从图中还可以看出，10叶片环形排列时稳定段压力梯度与单叶片涡流工具相近，导叶数增至12时压力梯度比单叶片要小。因此，就压力梯度而言，采用12叶片环形排列式涡流工具可以获得更好的降压效果。

另外，根据式

(6)

可计算出不同条件下稳定段的摩擦系数[23]，计算结果见表2。易发现摩擦系数随导流叶片数量和排布方式的变化规律与压力梯度相类似。式中：Δps为稳定段压降，Pa；ρm为混合流体密度，kg/m3；um为混合流体平均速度，m/s；D为管段直径，m；Ls为稳定段长度，m。

2.3 旋流强度衰减速率

旋流强度是描述螺旋流流动特性的一个重要物理量，其大小表征了流体旋转的强弱程度，与涡流工具的性能密切相关。螺旋流形成以后，在没有额外的旋流保持设施的情况下，旋转强度由于管壁的摩擦会逐渐衰减。Kitoh[20]和Najafi[24]等人的研究结果表明：平直管内稳定的螺旋流，其旋流强度随着流动的发展呈指数式衰减，具体可表述为

(7)

(8)

式中：S为测试点旋流强度；S0为参考点旋流强度；β为旋流强度衰减系数；R0为管段半径，m；Z为测试点位置，m；Z0为参考点位置，m；ut为流体切向速度，m/s；ua为流体轴向速度，m/s；r为径向坐标。

根据式(8)可以得到不同类型涡流工具下游沿程旋流强度分布，如图13所示。可见，涡流工具作用下流体旋流强度满足指数递减规律。而且环形排列方式下，参考点(Z0=200 mm)旋流强度随导叶数的增加而增大，连续排列则正好相反。因此，环形排列时参考点的旋流强度均大于连续排列。

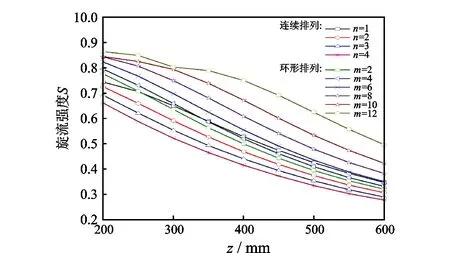
图13 涡流工具下游沿程旋流强度分布Fig.13 Distribution of swirl intensity in downstream of downhole vortex tool

对涡流工具而言，旋流强度衰减越慢，则螺旋流延伸距离越长，即涡流工具的有效作用距离越长。为了研究不同类型涡流工具下游流场旋流强度的衰减速率，将式(7)转化为

(9)

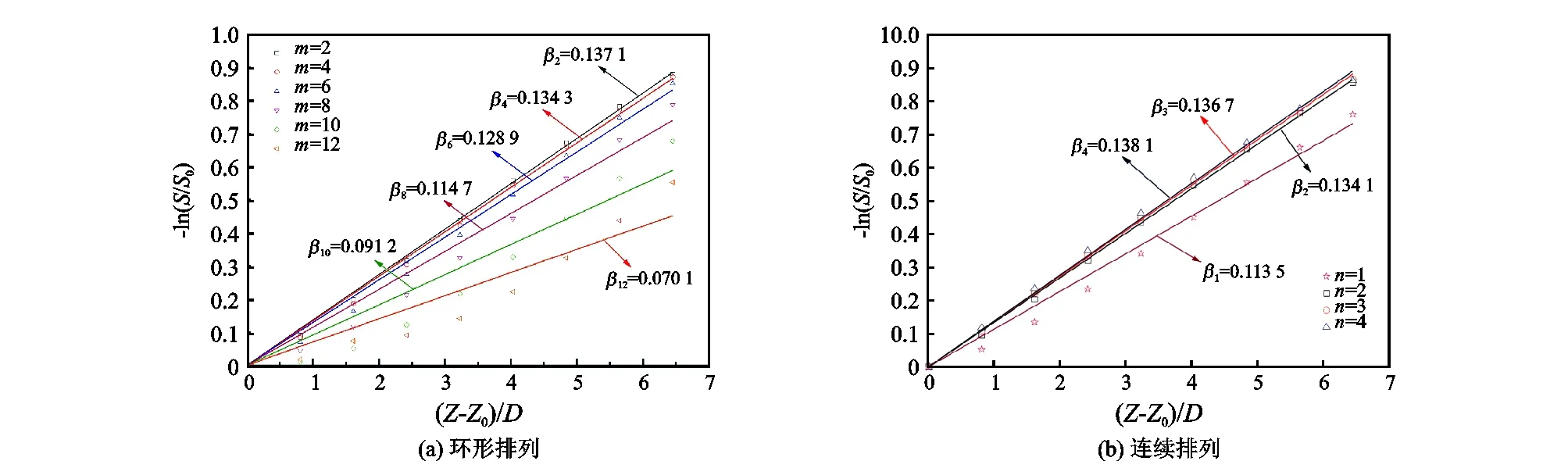
图14 不同导叶数下旋流强度衰减系数Fig.14 Decay rate of swirl intensity under different guide vane number

综合以上分析可以发现，连续排列方式下，单叶片涡流工具下游流场压力梯度最小，旋流强度衰减速率也最小；环形排列方式下，导流叶片数量越多，下游流场压力梯度和旋流强度衰减速率越小。12叶片环形排列式涡流工具下游旋流场平均切向速度比单叶片大，压力梯度和螺旋流衰减速率比单叶片小。因此，从降低工具下游流体压力梯度和旋流强度衰减速率考虑，可尝试将目前常用的涡流工具改进为12叶片环形排列式涡流工具。