二次螺旋斜弹簧的数学建模
2018-10-15
(大连理工大学数学科学学院,辽宁大连,116024)
1 引言
斜圈弹簧又名弹簧触指,最早由ABB发明并应用于开关行业。作为一种电接触形式以其结构简单、载流量大、体积小、成本低等众多优点,被广泛应用于电力、能源等行业。近年来又在斜圈弹簧的环圈结构基础上发展出二次螺旋结构的新形式,即二次螺旋斜圈弹簧。这种弹簧在保持斜圈弹簧原有电性能、可靠性的基础上大幅降低了制造成本,在新能源领域(充电桩)一些电连接器厂家正积极采用这种接触方式。
然而,欲对这两种弹簧进行3D建模却遇到了较大的困难,必须通过较复杂的数学建模写出这种异型螺旋线的参数方程。
根据螺旋线的结构可分为正弹簧和斜弹簧两种形式,又根据螺旋线中心轴走向可分为直线式、环圈式、(二次)螺旋式三种形式。组合后可得到六种螺旋线结构,如图1至图6所示。
本文拟以这六种弹簧,由简到繁逐步探讨其数学建模方法。

图1 直线正弹簧 图2 直线斜弹簧

图3 正圈弹簧 图4 斜圈弹簧

图5 二次螺旋正弹簧

图6 二次螺旋斜弹簧
2 直线正螺旋线与斜螺旋线
2.1 直线正螺旋参数方程
图1所示的直线正螺旋,其螺旋线是数学上常见的圆柱螺旋线,设r为螺旋线投影圆的半径,A为螺旋线的螺距。
写为矩阵形式:令X,Y,Z为坐标轴的基底,即X=(1,0,0)′ Y=(0,1,0)′ Z=(0,0,1)′。则其参数方程矩阵形式为:
转换为一般参数方程为:
(1)
2.2 直线斜螺旋参数方程
直线斜螺旋线的包络面和正螺旋线一样为圆柱形,区别在于Z轴方向进行了倾斜处理,我们可以在Z轴增加一项周期性扰动,即可达到使倾斜目的。
于是可以直接得到该螺旋线的一般参数方程为:
(2)
r与A的意义和正螺旋线一样,d是衡量倾斜多少的一个参数。
工程上习惯使用倾角θ描述螺旋的倾斜程度,下面讨论如何用θ取代式(2)中的参数d。用与正螺旋线相似的矩阵法,将X轴旋转θ。
取:X=(1,0,tanθ)′ Y=(0,1,0)′ Z=(0,0,1)′,有:
将其写为一般参数方程为:
(3)
在形式上和方程(2)无异,但解释了参数d的含义,θ为其倾角。对比方程(2)、(3),不难得出: d=rtanθ
3 环形螺旋线参数方程
接下来进行环形螺旋线的数学建模。前面讨论的直线形螺旋线均为沿着Z轴发展。而环形螺旋线却是按照圆形轨迹发展的,如图5。
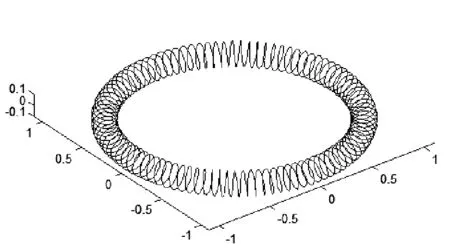
图5 环形螺旋线
设轨迹圆半径R,其轨迹圆的参数方程:
如何在轨迹圆上建立螺旋线呢?需要使用空间坐标转换,在轨迹圆上任取一点的切线(cost,-sint,0),以该切线为旋转轴,并在该旋转轴的垂直平面上建立一组正交基底:X=(sint,cost,0)′ Y=(0,0,1)′,根据螺旋线方程,我们便能写出在这组基底下的螺旋扰动,由于该扰动和轨迹圆的参数方程共用一个参数t,所以需要增加一个参数M来控制扰动螺旋的圈数,其参数方程矩阵形式为:
写为一般参数方程为:
(4)
其中R为轨迹圆半径,r为扰动螺旋半径(即小螺旋半径),M为扰动圈数。
4 二次螺旋线参数方程
4.1 二次正螺旋线参数方程
所谓二次螺旋线,就像将一根直线弹簧绕成一个更大的螺旋状,如图6。这里我们将大螺旋称为轨迹螺旋,小螺旋称为扰动螺旋。建模的方法是在轨迹螺旋线的基础上添加了一个扰动螺旋。其主要思想是将轨迹螺旋上任一点的切线方向作为扰动螺旋的旋转轴,再通过该点与旋转轴垂直的平面上建立一个正交坐标系。但在一个平面中有无穷多种建立正交坐标系的方法。这里我们规定将其中一个坐标轴与XOY平面平行,这样这个坐标系就可以唯一确定。下面是具体过程。

图6 二次螺旋线
令轨迹螺旋线的参数方程为:
则任一点切线方向为(cost,-sint,A/2Rπ),我们取与之垂直且与XOY平面平行的线的方向X′=(sint,cost,0),最后我们就可以唯一确定一条与前面两条线都垂直的方向Y′,注意要将Y单位化。参数方程矩阵形式为:
其中R为轨迹螺旋线半径,A为轨迹螺旋线截距,r为扰动半径,M为扰动螺旋的圈数。
将其写成一般参数方程的形式:
4.2 二次斜螺旋线参数方程
二次螺旋斜弹簧(图6)的数学建模是本文最终的目的。我们已有二次正螺旋方程式(5),当前的任务是在式(5)基础上将扰动螺旋进行倾斜。我的思路是,在选择扰动螺旋的坐标系基底时,偏转其X轴和Y轴,达到扰动螺旋倾斜的目的。其参数方程矩阵形式如下:
由于扰动螺旋是斜螺旋,故式中X,Y的选取并非正交的,但是同样能达到螺旋旋转的目的。
由于扰动螺旋半径在正螺旋和斜螺旋中的定义有所区别,为方便调用,使用MATLAB进行建模。自定义myfun函数(参见附录:myfun(a,b,h,c,d,e,f,g))
共设置了8个控制变量,其含义如下:
a为轨迹螺旋半径;b为轨迹螺旋螺距;h为扰动螺旋形状(h=1时,扰动螺旋包络面为圆;h=0时,扰动螺旋包络面为椭圆,即该螺旋线在二次螺旋形变前为正螺旋线);c为扰动螺旋半径(h=1时,为包络面半径;h=0时,为二次螺旋形变前的正螺旋半径);d为轨迹螺旋一圈扰动螺旋圈数;e为轨迹螺旋轴向方向二次螺旋的偏角;f为轨迹螺旋切线方向二次螺旋的偏角;g为参数t的最大取值(即轨迹螺旋的总长度)。
得到二次斜螺旋线如图7:

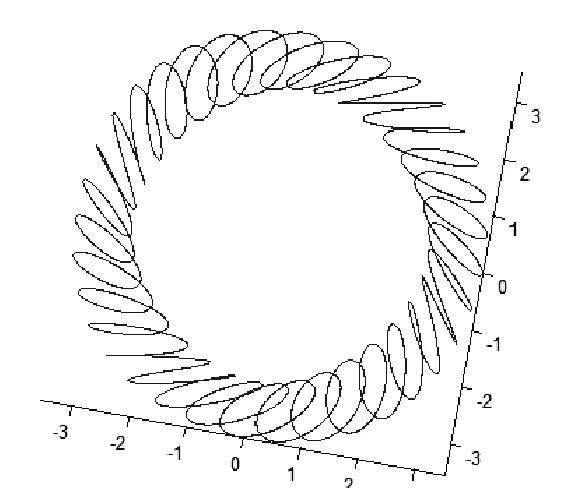
图7 二次斜螺旋线
最后在MATLAB中将该曲线输出为一个点阵txt 文件,再通过三维CAD软件输入该点阵txt文件,即可建立该曲线模型。
5 结束语
本文由圆柱螺旋线入手,逐步探讨了正、斜螺旋、环圈螺旋、二次螺旋的变形特点,梳理出若干特征参数,通过空间坐标变换方法成功实现了这六类螺旋的数学建模。并通过自定义的控制变量可以实现螺旋线的大、小直径、螺距、形状、倾角等参数的自由调节,方便产品设计师任意更改螺旋参数。解决了本类螺旋线建模的数学问题。
附录
4.2中的myfun函数:
function [x,y,z]=myfun(a,b,h,c,d,e,f,g);
t=0:1/1000:g;
if h==0
x=a*sin(t)+(c/cos(e))*sin(d*t).*(cos(e)*cos(t)/sqrt(1+(a/b)^2)+sin(e)*cos(t)/sqrt(1+(b/a)^2))+(c/cos(f))*cos(d*t).*sin(t+f);
y=a*cos(t)-(c/cos(e))*sin(d*t).*(cos(e)*sin(t)/sqrt(1+(a/b)^2)-sin(e)*sin(t)/sqrt(1+(b/a)^2))+(c/cos(f))*cos(d*t).*cos(t+f);
z=b*t+(c/cos(e))*sin(d*t)*(-cos(e)*(a/b)/sqrt(1+(a/(b))^2)+sin(e)*(b/a)/sqrt(1+(b/a)^2));
elseif h==1
x=a*sin(t)+c*sin(d*t).*(cos(e)*cos(t)/sqrt(1+(a/b)^2)+sin(e)*cos(t)/sqrt(1+(b/a)^2))+c*cos(d*t).*sin(t+f);
y=a*cos(t)-c*sin(d*t).*(cos(e)*sin(t)/sqrt(1+(a/b)^2)-sin(e)*sin(t)/sqrt(1+(b/a)^2))+c*cos(d*t).*cos(t+f);
z=b*t+c*sin(d*t)*(-cos(e)*(a/b)/sqrt(1+(a/(b))^2)+sin(e)*(b/a)/sqrt(1+(b/a)^2));
end
plot3(x,y,z)
axis equal;
