基于Wiener过程的独立部件精度预测方法

张 优，胡昌华，李红增，扈晓翔，白 灿，张 鹏

(火箭军工程大学控制工程系，陕西 西安 710025)

0 引 言

由于外界环境、人为测量活动及设备自身老化磨损[1]等的影响，测量设备的精度随时间不断损失。当该损失达到一定程度时，测量系统不再满足测量精度的要求，其寿命也随之终结。但是，系统内部各个组成单元由于材料、性质、结构、性能等不同,造成其动态精度损失的规律也不同。有的部件的精度损失可能较小，可以继续使用，而有的可能已经报废。这样就给设备的校准和更换活动带来了很大的困难，也造成了资源的浪费和成本的提高。同时，大多数测量设备因为自身设计的缺陷及原位测量的要求，其内部各部件的精度不可直接测量。因此，针对不可直接测量的一类设备，研究动态测量系统内部各部件的误差传递情况，做好精度预测方面的工作，确保整个测量系统在一个寿命周期内正常运行是具有重大实际意义的。

针对存在上述问题的测量设备，首先对总误差进行成分分离，得到各部件的误差统计量后，再进行精度预测。目前常用的动态误差分解的方法[3-4]有独立成分分析、自适应滤波、小波分析、神经网络、希尔伯特-黄变换等，应该根据实际情况合理运用这些方法。

现阶段对动态精度损失的预测主要是基于数据驱动[2]的方法，分为基于机器学习的方法和基于概率统计的方法。近些年，基于机器学习的方法在精度预测方面运用较多。文献[5]提出了基于标准量插入动态实时误差修正的灰色理论与方法，达到预测与修正的目的；文献[6]提出了基于最小二乘向量机（LS-SVM）的方法对航空发动机的气路参数进行在线预测；文献[7]分别将最小二乘拟合法、神经网络、灰色理论和支持向量机这4种方法应用于精度退化预测，并分析了各自的优缺点和适用范围。这些方法拟合精度较高，但存在长期预测精度较差，只能给出点估计，显然不满足动态特性的要求。相比之下，概率统计类的预测方法主要是基于随机过程、统计推断等理论形成发展而来，不仅能给出点估计，还能给出预测结果的概率分布，更能体现动态特性。文献[8]利用贝叶斯模型对精度退化进行预测；文献[9]提出根据历史校准数据估计参数，建立威布尔可靠性模型来对计量周期进行预测。

基于上述研究，结合实际中动态测量系统内部各部件精度损失规律的差异性，本文提出一种基于随机维纳过程的独立部件剩余精度预测方法。利用极大似然估计法得出参数的初始解，再用贝叶斯方法实现参数的在线更新，进而预测系统各部件的精度损失情况。

1 误差传递模型

根据全系统理论[10]，动态测量系统是由若干传递单元组成，通过传递链函数可将系统物理性质进行“白化”,并在此基础上反映系统输入与输出之间的关系。基于此，建立整个系统由总输入到总输出的误差传递模型，其表达式为

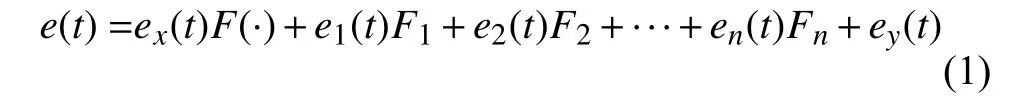
其中，e(t)是动态系统输出的总误差；ei(t)是第i个单元的误差；ex(t)和ey(t)分别为输入输出的噪声误差；F(·)是整个系统的传递函数；Fi是当前第i个单元到总输出的传递链函数。

根据全系统动态误差建模理论以及系统总误差规律,采用现代数学分析方法,经过分解和溯源[10]得到测量系统各个部件的误差变化规律。通过间接测量的方法得到各个部件的精度损失统计量，再进行精度预测。

根据动态测量系统实际误差测量,得系统总体动态精度损失序列为

再经过误差的分解与溯源，得到各个结构单元动态精度损失序列为

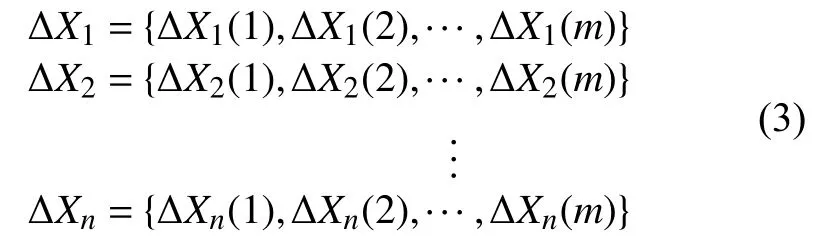
其中，1,2,···,m为 时间序列，1,2,···n为分量序列。

在本文中，以误差的均值作为精度损失的统计量。每个单元损失项对系统总的精度损失都有贡献,其贡献的程度不仅与各个单元的单项精度损失量Δei有关，还与各个单元的全系统结构误差传递链函数Fi有关。因此，各个单元精度损失对系统总精度损失的影响程度是该单元的Δei与Fi的乘积。

2 基于Wiener过程的精度损失模型

动态测量系统在不同测量阶段的精度损失一般是非严格单调、非平稳的趋势序列。根据研究，在t到t+Δt时间段内，系统各部件的精度损失量Δei是由相互独立同分布的随机微小损失量累加而成的，并且微小损失量的数目与时间成正比，即Δei服从正态分布。因此，可认为部件精度损失过程服从一元Wiener过程[11]。

动态测量系统内部各单元的精度损失量首次超过失准阈值D（一般取精度极限指标Dlim的90%）时，则可以认为该单元失准。定义在ti时刻的剩余精度为Li，其具体实现为li：

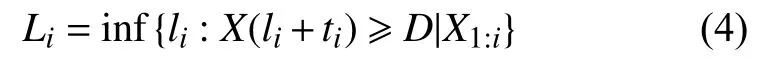
根据文献[12]，模型可表示为

其中，X(t)表示tD(tD＞ti)时刻的精度退化量，tD为失效时间；xi为在ti时 刻的精度退化量；λ表示Wiener过程的漂移系数，本文假设 λ服从正态分布，即λ∼N(µλ,σ2λ)；σ表示扩散系数；β(li)是标准布朗运动。

同时，剩余精度的概率密度函数和累计密度函数为

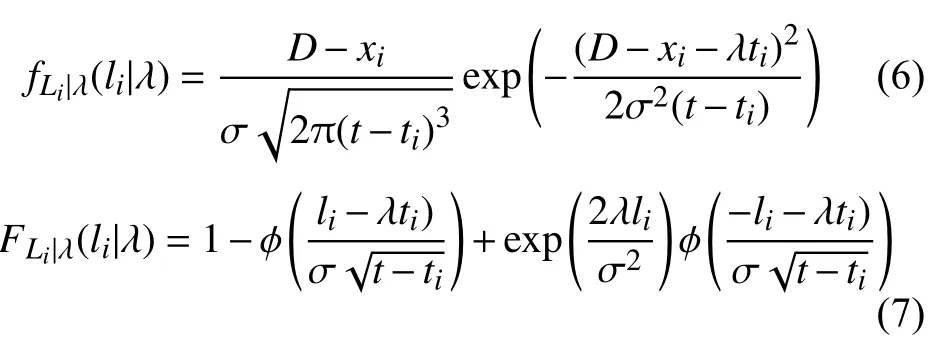
令精度损失增量，由Wiener过程的齐次马尔科夫性可得 的概率密度函数为Δξi=Xi−Xi−1Δξi

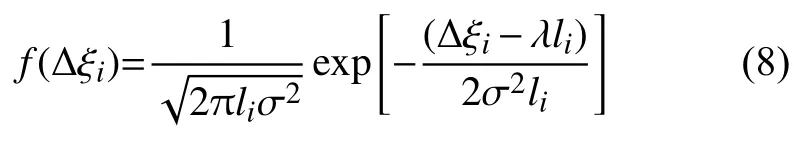
3 参数估计与精度预测

定义参数量θ=[µλ0,σ2λ0,σ2]T，其中，µλ0，σ2λ0为漂移系数 λ的均值和方差。可以通过实时测量得到实测数据，并对历史数据和在线数据进行误差的分解与溯源工作，这样就得到了模型参数估计的统计量。基于此，考虑参数的估计分为两部分：1）用MLE方法处理离线数据，得到参数初始值，为方便起见，仍然记为 θ=[µλ0,σ2λ0,σ2]T；2）用贝叶斯估计方法对参数 λ进行在线更新。

3.1 参数的离线估计

根据前文，假设经{过误差分解与}溯 源得到误差源的误差数据序列为X(ti),1≤ti≤tf，其中，tf为离线数据的总数。本文研究的对象是一类独立部件，无法以同类产品的历史数据作为参考，仅仅具有一组本身的实验数据。因此，根据文献[13]中提出的极大似然估计方法，应将其简化为一维状态。令t=(t1,···,tf)T，x=(x(t1),···,x(tf))T，x服从多变量高斯分布，均值和协方差分别为

其中

利用极大似然估计对 θ进行估计，对于精度损失序列X1:i建立对数似然函数如下：

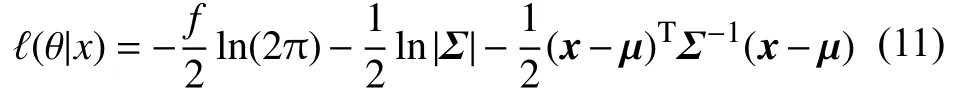
其中

极大化式（11）就可得到 θ 最优解θ=[µλ0,σ2λ0,σ2]T，也是参数的初始值，从而在此基础上实现贝叶斯方法更新随机参数 λ。

3.2 在线参数更新

为了体现各部件的个体差异性，将3.1节求得的最优解 θ作为λ的先验分布。在tk时刻，通过数据处理得到所有误差数据为

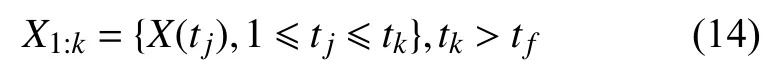
采用贝叶斯统计推断模型[14]，得出λ 的后验分布为

因此，tk时刻对随机参数λ的更新结果为

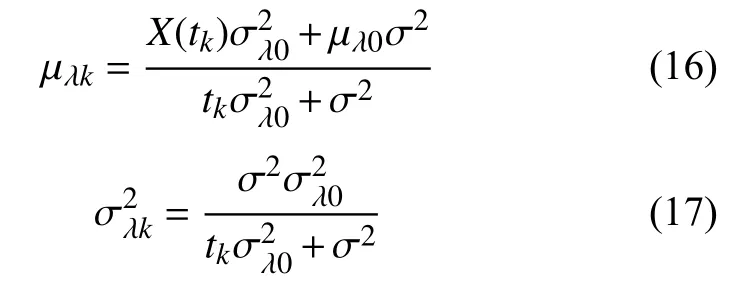
根据式（16）、式（17）就可以对每次新获得的数据进行在线实时更新。基于此，给出剩余精度在tk时刻的概率密度函数，其表达式为

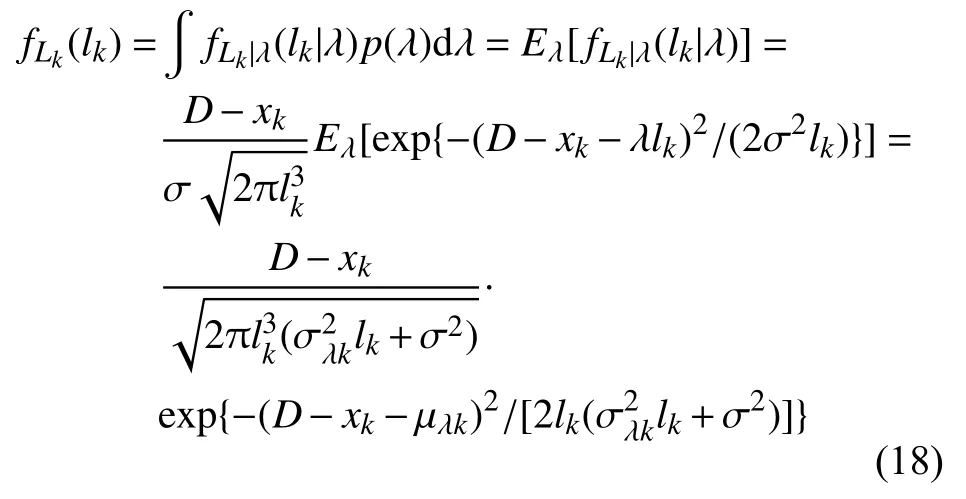
3.3 精度损失预测模型算法

根据上述分析，能够得到精度损失预测模型算法，步骤如下：

1）根据全系统理论，利用式（1）～式（3），得到系统总误差后，对系统误差进行动态误差分解与溯源，得到各部件的误差统计量。

2）参数的离线估计。根据步骤1）得到的统计量，对独立部件利用MLE（式（11））方法求出 θ的初始分布。

3）参数的在线更新。在步骤2）得出的初始值条件下，根据tj时 刻获得新的单元误差数据ei(tj)，利用贝叶斯推理（式（16）、式（17））实现参数递推求解。

4）根据参数的更新结果，利用式（18）求得剩余精度的概率密度函数，从而实现系统内部各部件的剩余精度的在线预测。

4 实例验证

为验证本文提出预测模型的精确性和描述精度退化过程不确定性的合理性，根据蒋敏兰等[7]研究的百分表误差测量数据进行实验分析。百分表长期使用以后，由于其内部各结构单元的磨损使得测量精度不断下降。内部结构单元的误差主要包括侧头磨损误差、测杆与套筒磨损引起的误差、测杆和齿条环节的误差、轴齿轮副环节的误差和中心齿轮和表盘的误差。在实验过程中，发现在81组之后的实验数据已经超出允许范围了，所以只取前80组的经过误差分解与溯源之后的实验数据来对百分表进行研究，以前3个分量（测杆和齿条环节的误差特性、轴齿轮副环节的误差特性、中心齿轮和表盘的误差特性）为例，如表1所示。

测杆和齿条环节的误差特性为

轴齿轮副环节的误差特性为

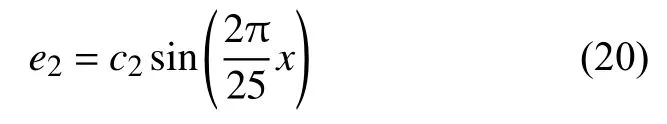
表1 3个分量的测量数据

中心齿轮和表盘的误差特性为

其中，x为百分比全量程的采样点，x=1,2,···,25，c1、c2、c3为常值。

本文取前70组数据作为部件精度退化的离线数据，后10组数据作为在线数据。运用本文的方法对分量1、2、3进行预测，结果如图1所示。

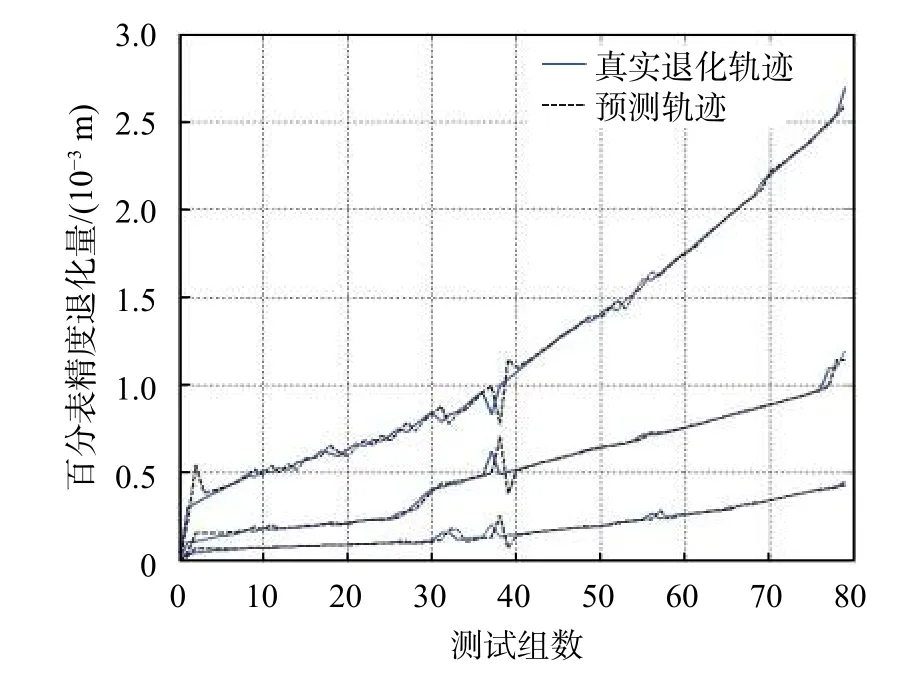
图1 分量1、2、3的精度退化预测轨迹

从图中可以看出，百分表各单元由于结构磨损等因素影响，总体呈现上升的趋势，但并非严格服从单调递增。为了验证精度损失数据是否符合Wiener过程特点，再对其进行Kolmogorov-Smirnov（K-S）检验，置信度为95%，检验结果如表2所示，表明数据符合正态分布，可以使用本模型。

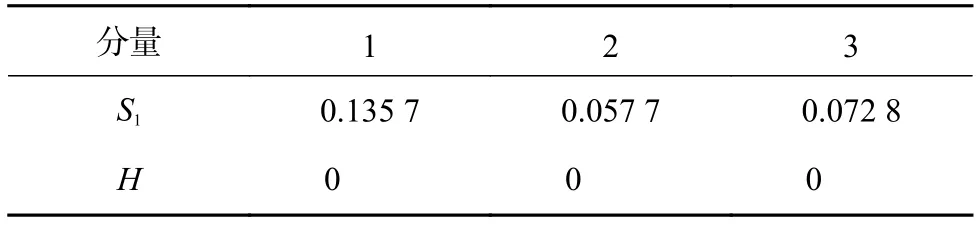
表2 K-S检验结果1）

以分量1为例，运用本文提出的贝叶斯更新方法即可得到其精度的概率密度分布。针对第71～77个检测数据，图2给出了其概率密度分布图。

图2 分量1第71～77个数据的PDF

由图可知，分量1的第71～77个数据监测点的剩余精度分布的集中程度明显提高，主要原因在于随着百分表随测量活动精度损失不断累计，剩余精度的不确定性不断减少，与此同时，预测的准确性不断提高。为了验证本方法预测的准确性，引入均方误差（MSE）指标，定义[13]如下：

其中，xk示在tk时刻的实验值，x′k表示在tk时刻预测的退化值。得出MSE为4.495 2×10-4，这说明模型能够有效表征独立部件的精度退化过程。

同时，引入剩余精度预测的均方误差：

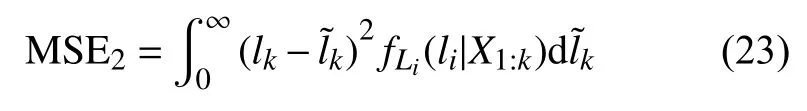
图3 分量1的剩余精度均方误差

从图中可以看出，本文提出的方法能够准确地预测系统内部各部件的精度，并且随着参数的更新，预测的准确性不断提升。

5 结束语

本文根据动态测量系统精度退化过程的特性，提出系统内部各单元的精度退化过程服从Wiener过程。基于极大似然估计方法和贝叶斯方法，提出了一种实时预测的动态误差预测模型，为校准维护等活动的开展提供了依据。根据实验结果，得出如下结论：1）本文方法在保证预测精度和较小的不确定性基础上，给出了预测结果的概率分布，更加符合动态测量的实际特点；2）该方法依赖于间接测量提供数据的准确性，因此下一步工作应着重于提高动态误差分解与溯源方法的准确性。