Voronoi图混合栅格算法改进研究

2018-10-15沙俊淞王秋实张学军王斌君

中国人民公安大学学报（自然科学版） 2018年1期

沙俊淞, 王秋实, 张学军, 王斌君

(1.中国人民公安大学信息技术与网络安全学院，北京 100038； 2.公安部第一研究所物联网部，北京 100048)

0 引言

Voronoi图是计算几何的一个重要分支。计算几何中的voronoi图常被用于解决地理学、气象学、移动通信等领域的选址优化、空间划分、路径规划等问题。此外Voronoi图在考古、生态研究、城市规划等领域也有广泛的应用[1]。在公安领域内，通过构造关于基站分析的分区加权Voronoi图，有助于公安机关更加准确地确定侦查范围。

随着社会的高速发展，普通的Voronoi图已经无法满足实际应用的需要。所以，研究者们在Voronoi图的基础上扩展出了加权Voronoi图[2]、分区加权Voronoi图[3]等。

对于分区加权Voronoi图，主要有两种栅格生成算法：逐点扫描法[4]和模拟生长法[5]。逐点扫描法的基本思想是：通过计算平面上所有点与生成元的距离来生成Voronoi图。后人根据分区加权Voronoi图的定义，提出了适用于分区加权Voronoi图的逐点扫描算法[6]。模拟生长法的基本思想是：将空间生长目标作为圆心，不断向四周扩张占领空白像素，直到所有区域被覆盖。根据分区加权Voronoi图的定义，马立玲在原方法的基础上，提出了分区加权Voronoi图的模拟生长算法[3]。

1 基本概念和算法介绍

1.1 基本概念

1.1.1 Voronoi图

定义1：设S={p1,p2, …,pn}为平面上n个互不相同的点集，由：

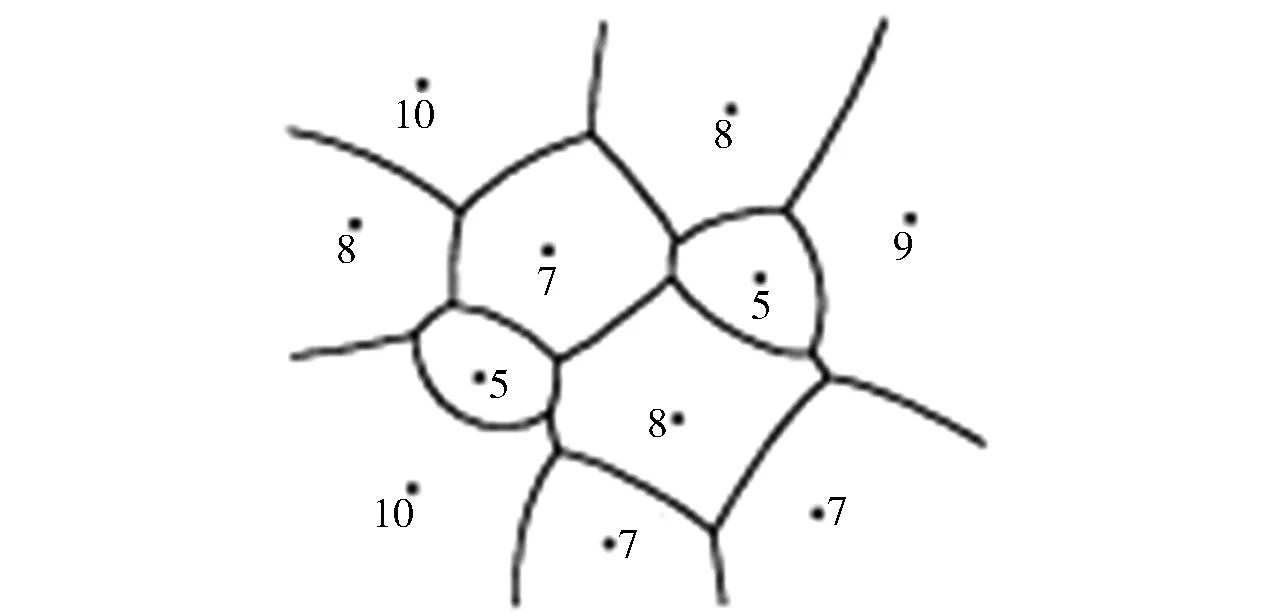
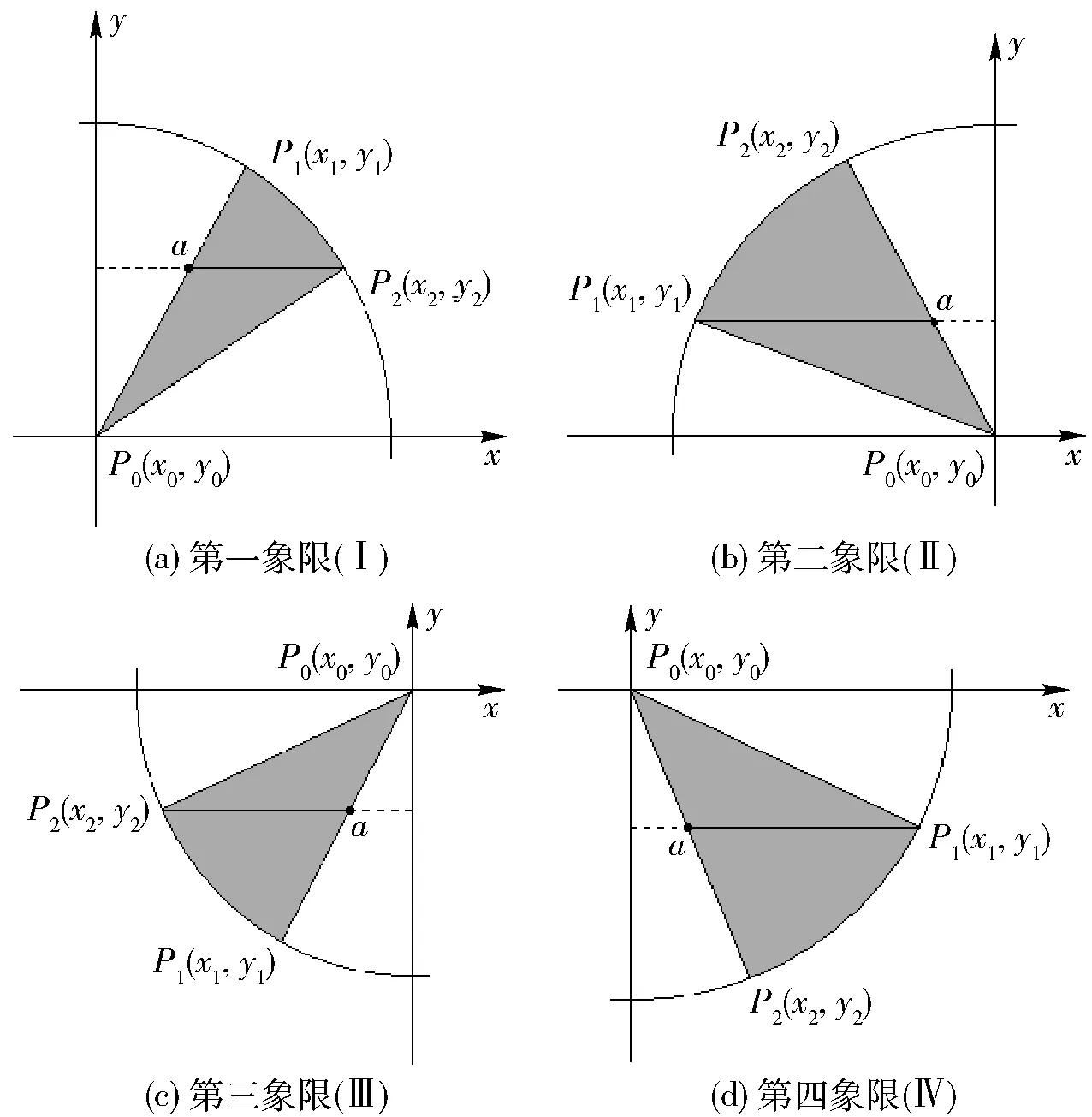
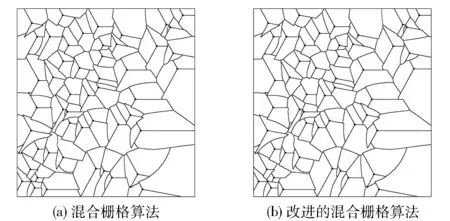
Vn(pi)={p|d(p,pi)

所给出对平面的分割，称为以pi(i=1,2,…,n)为生成元(或母点)的Voronoi图，简称Voronoi图。其中d(p,pi)称为p和pi之间的Euclid距离。区域V(pi)称为pi的Voronoi区域[4]。同时，在pi的Voronoi区域内的所有点到pi的距离比到其他母点的距离都更近。图1是一个Voronoi图的示例。

图1 Voronoi图

1.1.2 加权Voronoi图

定义2：设S={p1,p2, …,pn}为平面上n个互不相同的点集，对每个生成元p1,p2, …,pn赋以非负实数权重λ1,λ2, …,λn。称D(p,pi)=d(p-pi)/λi为p和pi之间的加权距离。称

(i,j=1,2,…,n)

为点pi的权重为λi的加权Voronoi区域。将V(pi，λi)(i=1, 2, …,n)及其边界，称为以p1,p2, …,pn为生成元(或母点),以λ1,λ2, …,λn为权重的加权voronoi图[4]。图2是加权voronoi图的示例，图中的数字代表每个生成元的权重。

图2 加权Voronoi图

1.1.3 分区加权Voronoi图

定义3：设S={p1,p2, …,pn}为平面上n个互不相同的点集，对每个生成元pi，以pi为原点，水平向右为坐标轴的正向，建立极坐标系，将生成元pi周围区域分为mi个扇区，以θ=αij(j=1,2,3,…,mi)为扇区分界线，其中0≤αi1<αi2<αi3…≤2π，并给每个扇区赋以权重λij(j=1,2,3…mi)。称

(i,j=1,2,…,n)

(当j≠mi时，p在射线θ=αij与θ=αi(j+1)之间；当j=mi时,p在射线θ=αi1与θ=αimi之间)为点p在第j扇区权重为λij的Voronoi区域。将V(pi,αij,λij) (j=1,2,3…mi) (i=1,2,3…n)及其边界称为以pi(i=1,2,3…n)为生成元或母点，以(λi1，λi2，…λim)(i=1,2,3…n)为相关扇区权重的分扇区加权Voronoi图，简称分区加权Voronoi图[3]，图3是分区加权Voronoi图的示例。

图3 分区加权Voronoi图

1.2 混合栅格算法

通过研究发现：逐点扫描法结果准确，但效率较低，一般用于生成元数量少且范围和边界要求严格的应用领域；而对于生成元数量较多，但范围和边界要求不严格的应用领域，则一般采用效率更高但结果不够准确的模拟生长法。

针对逐点扫描法和模拟生长法的优缺点。王斌君教授提出了一种生成分区加权Voronoi图的混合栅格算法。其基本思想是：对于平面上的生成元，首先对生成元进行预处理，预处理环节是通过预先扩展一定大小的覆盖区域，相当于每个生成向外扩展一大步；然后，对每个生成元扇区扩展的覆盖区域按照特点的颜色着色，同时将相交区域内的点置白；最后，对剩余像素和相交区域按照原逐点扫描法进行处理，生成分区加权Voronoi图。

混合栅格算法在提高效率的同时，又保证了精度，可以很好的满足生成元数量多且对范围和边界要求严格的领域。但是，该算法在重叠区域处理方面不够精细，增加了算法的时间复杂度的描述。所以，针对这个问题本文提出了一种改进算法。

2 改进的混合栅格算法

在文献[6]的混合栅格算法中，对生成元扇区进行预处理的相交部分用逐点扫描算法进行处理虽然正确，但存在冗余。这是因为，重叠区域点的隶属问题不需要按照原始的逐点扫描法计算重叠区域点与所有生成元之间的距离，只需与曾覆盖该点的生成元扇区进行计算即可。通过这个方法可进一步降低混合栅格算法的时间复杂度，提高算法效率。

2.1 数据结构设计

算法涉及的主要数据结构是生成元和重叠区域点的数据结构：Generator记录各生成元的二维坐标、各扇区起始角度、权重和颜色等信息；AllGen是一个包括所有生成元的数组；spot记录离每个重叠区域内点加权距离最近的生成元编号和扇区编号，Overlap[,]是一个包括平面上所有点的二维数组。

structGenerator

{

x; ∥生成元x坐标

y; ∥生成元y坐标

w[]; ∥生成元扇区权重

a[]; ∥生成元扇区角度

RGB[][3];∥生成元扇区颜色

} AllGen[];

Struct spot

{

I; ∥生成元编号

j; ∥生成元扇区号

}OverLap[,]

2.2 算法设计

算法1：重叠区域隶属计算算法

输入:当前生成元编号CurI，当前生成元扇区号CurJ，重叠点坐标(CurX,CurY)

输出:null

S1:∥初始化

OldI = OverLap[CurX,CurY].i;

OldX = AllGen[ OldI].x;

OldY = AllGen[ OldI].y;

OldJ = OverLap[CurX,CurY].j;

OldW = AllGen[OldI].w[OldJ];

CurW = AllGen[CurI].w[CurJ];

S2:∥计算(CurX,CurY)到两生成元的加权距离

OldD=(float)(Math.Sqrt((CurX-OldX)·(CurX-OldX)+(CurY-OldY2)·(CurY-OldY)))/OldW;

CurD=(float)(Math.Sqrt((CurX-AllGen[CurI]·x)·(CurX-AllGen[CurI].x)+(CurY-AllGen[CurI].y)·(CurY-AllGen[CurI].y)))/CurW;

S3:if (CurD

将CurI和CurJ存入OverLap[CurX,CurY];

}

S4:结束

经典的区域填充算法主要有两种，一种是通过确定横跨区域的扫描线的覆盖间隔来填充的扫描线算法[7]，另一种是从给定的位置开始填充直到指定的边界为止的种子填充算法[8]。而本算法涉及的填充域着色是一个关于扇区的填充问题。所以，设计了一种简单而高效的扇区填充域算法。

首先，考虑简单情况，即仅需要填充的扇区只在某一个象限。如图4所示的4种情况，分别对应算法2.1、算法2.2、算法2.3和算法2.4。

图4 单象限的扇区

算法2.1：填充扇区只在第一象限

输入:圆心(x1、y1)，角度α1，角度α2，半径r，颜色c[3]

输出:对给定的第一象限扇区按颜色c填充着色，重复区域调用算法1

S1: if (α1==0) 从(x1,y1)到(x1+r,y1)画线; ∥画线就是在两点之间依次对点着色，如果该点是白色则将其置为颜色c，若不是则调用算法1

else将点(x1,y1)置为颜色c;

S2:for (y=y1;i≤y1+r·sin(=α2);y++) { ∥从y=3到y=y2逐行画线

x1=x1+y·tan(α1);

x2=x1+y·tan(α2);

从(x1,y)到(x2,y) 画线;

}

S3:for(y=y1+r·sin(α2)+1;i<=y1+r·sin(α1);y++) { ∥从y=y2到y=y1逐行画线

x1=x1+y·tan(α1);

x2=sqrt(r·r-y·y);

从(x1,y)到(x2,y)画线;

}

S4:结束

算法2.2、算法2.3和算法2.4的基本思想与算法2.1相同，不再赘述。

然后，再考虑一般的情况，即需要填充的区域跨象限。先把扇区按照象限划分为若干个处于同一象限的子扇区，再对这些子扇区分别调用对应的算法2.1、算法2.2、算法2.3和算法2.4，即可完成对跨象限扇区的填充。例如，在图5中，扇区P0P1P2跨越了第一、第二和第三扇区，可分别用算法2.1、算法2.2和算法2.3填充P0aP2、P0ba和P0P1b，即可完成对P0P1P2扇区的填充。

图5 跨象限的扇区

算法2：扇区填充算法

输入:圆心(x1,y1)，角度α1，角度α2，半径r，颜色c[3]

输出:对给定的任意扇区按颜色c填充着色，重复区域调用算法1

S1:switch(α1) {

caseⅠ:switch (α2){

caseⅠ:算法2.1(x1,y1,α1,α2,r,c);

caseⅡ:算法2.1(x1,y1,α1,90,r,c);

算法2.2(x1,y1,90,α2,r,c);

caseⅢ:算法2.1(x1,y1,α1,90,r,c);

算法2.2(x1,y1,90,180,r,c);

算法2.3(x1,y1,180,α2,r,c);

caseⅣ:算法2.1(x1,y1,α1,90,r,c);

算法2.2(x1,y1,90,180,r,c);

算法2.3(x1,y1,180,270,r,c);

算法2.4(x1,y1,270,α2,r,c);

}

caseⅡ:…∥与Ⅰ相似，不再赘述。

caseⅢ:…∥与Ⅰ相似，不再赘述。

caseⅣ:…∥与Ⅰ相似，不再赘述。

}

S2:结束

算法3 改进的混合栅格算法

S1:∥初始化环节

将屏幕初始化为白色

S2:∥预处理环节

S2.1:设定一个经验参数k;

S2.2:for (对每一个生成元i的每个扇区j) { ∥所有生成元的初始覆盖

S2.2.1:R=k·AllGen[i].w[j];

S2.2.2:算法2

(AllGen[i].x,AllGen[i].y,AllGen[i].a[j] ,AllGen[i].a[j+1],R,AllGen[i].a[j].RGB);

}

S2.3:for (OverLap中的非空元素) {

根据对应生成元扇区的颜色进行着色;

}

S3:∥计算剩余点环节

for (扫描所有空白像素点){

按照逐点扫描法着色;

}

S4:∥确定边界环节

扫描绘图区域，抽取边界，得到分区加权Voronoi图;

S5:结束

3 实验结果及分析

实验平台的处理器为Intel(R)Core(TM) i5-5257U CPU@2.70GHz，内存8GB。开发平台是Visual Studio 2010，编程语言为c#。实验分别实现了模拟生长法、逐点扫描法，以及混合栅格算法和本文的改进算法。各组测试点集都是随机生成点集。表1是几种算法在不同分辨率和生成元数量下的时间效率。