基于局部学习的差分隐私集成特征选择算法
2018-10-15刘中锋
刘中锋
(南京邮电大学 计算机学院、软件学院、网络空间安全学院,江苏 南京 210000)
0 引 言
特征选择是机器学习和数据挖掘等领域的一个关键问题,是从一组特征中挑选出一些最有效的特征以降低特征空间维数的过程。特征选择不仅能够降低特征维数,也能够加快机器学习或者特征选择算法的执行速度,同时提高算法的准确率,使算法更具有可理解性。在之前的工作中,对于特征选择的研究主要集中在特征选择算法的稳定性[1]以及分类准确率等方面[2-3],然而隐私保护也是一个非常重要的研究方向,比如医院电子病历记录病人基本信息、疾病信息以及药品购买记录等,这些信息的泄露会对人身安全造成威胁[4]。虽然关于隐私保护的分类和回归等应用[5]都已着重研究过,但是对于隐私保护的特征选择算法的研究却很少[6-7]。已研究过的隐私保护仅仅是单特征选择算法,未涉及多个算法的领域。
与集成学习类似,集成特征选择算法也分为两个步骤:第一步是构造基特征选择器[8],第二步是通过某种组合集成每个基特征选择器的输出结果。文中采取Bagging集成策略,利用bootstrap抽样方法对原始数据集进行抽样,在抽样后的数据集上基于局部学习来训练基特征选择器[9],并且采取线性组合的方式对结果进行集成。为了使集成特征选择具有隐私保护的效果,利用输出干扰策略,提出了先对结果集成后添加噪声的集成特征选择算法FELP。证明该算法满足差分隐私模型[10-11]的定义,并通过实验证明其效用性。
1 基于局部学习的差分隐私集成特征选择算法
1.1 基于局部学习的特征选择
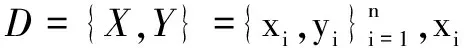
l(wTzi)=log(1+exp(-wTzi))
(1)
其中,w为特征权重向量;zi=|xi-NM(xi)|-|xi-NH(xi)|。zi可以看作是xi的变换点,wTzi可以看作是局部间隔,属于假设间隔[12]。此外,为了防止过拟合,在公式中加入了正则化项。由于L2正则化项具有旋转不变性[13],同时也具有很强的稳定性,所以评价准则定义为:
(2)
其中,λ为正则化参数。
基于局部学习的特征权重算法FWELL的内容见文献[14]。
1.2 差分隐私模型和敏感度
文中采用差分隐私模型[10-11]作为隐私风险的一个度量。差分隐私算法定义如下:
定义1(ε-差分隐私):对于任意给定的数据集D和Di(其中D和Di最多只有一个元素不同),以及任意的输出子集S⊆Range(F),如果有:
P[F(D)∈S]≤eε×P[F(Di)∈S]
(3)
则算法F满足差分隐私。
因为加入噪声的多少会影响算法的性能,所以基于差分隐私算法的输出干扰策略和算法的敏感度相关。文献[4,15]中对敏感度进行了定义。
定义2:对于任意带有n个输入值的算法F,全局敏感度ΔQ定义为对所有的输入值,当算法F的某个输入值变化时函数值的最大变化的L2范数,即:
(4)
式4的敏感度定义和文献[16]中算法稳定性的定义类似,该稳定性定义为:
(5)
式4和式5的区别在于,敏感度的定义旨在改变一个样本,而稳定性的定义旨在移除一个样本。根据三角不等式,能得到两者之间的关系,结论如下:
ΔQ=‖F(D)-F(D/i)-(F(Di)-F(D/i))‖≤‖F(D)-F(D/i)‖+‖F(Di)-
F(D/i)‖=2ΔSt
(6)
1.3 先集成后扰动策略的差分隐私特征选择算法(FELP)
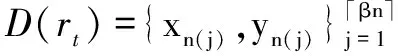
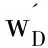
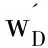
(7)
因为r1,r2,…,rk是独立同分布的,所以r1,r2,…,rk与r有相同的分布,根据三角不等式,则
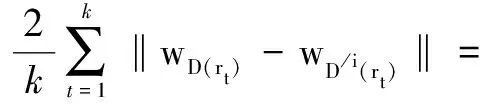
2‖wD(r)-wD/i(r)‖
(8)
故在数据集D(r)上,根据式5得到FWELL-EN的稳定性是‖wD(r)-wD/i(r)‖。因此可以得到:
ΔQ≤2‖wD(r)-wD/i(r)‖(I(i∈r)+I(i∉r))=2[‖wD(r)-wD/i(r)‖I(i∈r)+‖wD(r)-wD/i(r)‖I(i∉r)]
(9)
如果该索引r与i无关,也就意味着样本xi不在样本子集D(r)中,即满足D(r)=D/i(r),于是有wD(r)=wD/i(r)和‖wD(r)-wD/i(r)‖I(i∉r)=0。因此可得:
ΔQ≤2‖wD(r)-wD/i(r)‖I(i∈r)
(10)
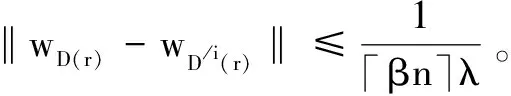
(11)
根据文献[11]中的噪声定义可知,敏感度为2/nλ的FWELL-EN算法的噪声向量bD定义如下:
(12)
其中,a为一个常量。
FELP算法的伪代码如下所述。
第一步:采取bootstrap抽样策略重复抽取k次(抽样参数为β),得到k个不同的样本子集,并且每个样本子集的大小是「βn⎤。
第二步:在每个样本子集上,根据算法FWELL得到k个输出结果wD。
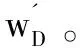
因为FELP算法是基于差分隐私的算法,所以该算法一定要满足差分隐私的定义,见定理1。
定理1:FELP算法满足差分隐私。
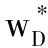
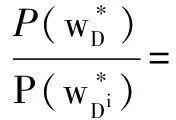
(13)
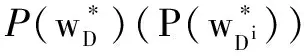
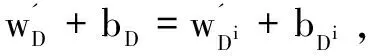
(14)
根据式11、13、14,可以得到:
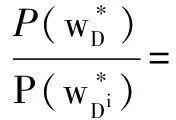
(15)
由上可知,算法FELP满足差分隐私。
2 实 验
文中采用FWELL-EN算法和FELP算法进行实验对比。整个实验包括两部分:验证隐私度参数ε的影响以及在某个特定隐私度的情况下,验证不同特征数量时的分类性能。在该实验中,选取支持向量机(SVM)和k近邻(kNN)作为分类器,SVM中参数C=1,k近邻分类器中的参数K=3。采用十次交叉验证,将数据集分为10等份,9份作为训练数据,1份作为测试数据。使用bootstrap抽样策略将训练数据集分为20个样本子集(k=20),并且每份抽样比例是β=0.9,所有实验中使用的参数λ将根据交叉验证调节。选取四个不同大小、不同维度的数据集作为实验数据,包括Arcene、Soybean、Wdbc和Breast,其中Arcene是一个典型的高维度的小样本数据集。
2.1 隐私度实验
该实验中选定的特征维数是原始数据集中特征维数的10%。FELP算法中的隐私度由ε衡量,ε值的增加意味着隐私度的降低,保护效果也越差。实验结果见图1。为了节省空间,两个分类器的结果共同显示在一张图中。
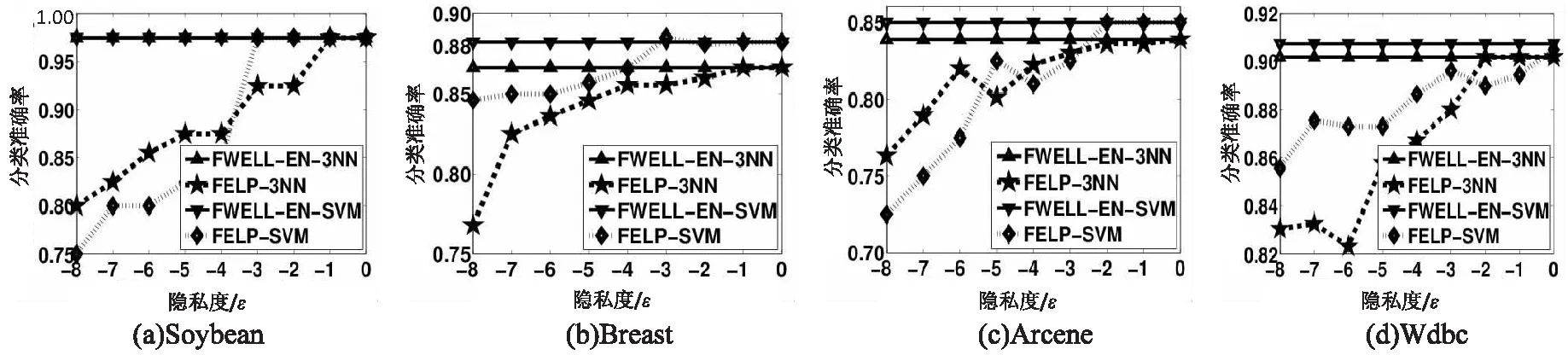
图1 隐私度实验结果3NN-SVM
从实验结果可以看出,在没有隐私保护的情况下(即ε=100),FWELL-EN算法的分类准确率和具有隐私保护效果的FELP算法有相同的值。但是随着隐私度ε的减小,算法FELP的分类准确率也随之减小,而隐私保护性能逐步提高。并且从整体上看,SVM分类器的准确率比3NN要高。虽然当隐私度越小时,隐私保护效果越好,但同样也面临可用性的降低,所以考虑到隐私保护和可用性的平衡,ε=0.01是一个效果不错的选择。
2.2 特征维数实验
该实验主要研究的是特征维数和分类准确率的情况,此时选定的隐私度ε=0.01。特征维数是根据数据集的特征维数来选取的。分类结果见图2。
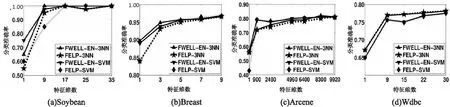
图2 特征维数实验结果3NN-SVM
从实验结果可以看出,在特定的隐私度ε=0.01时,算法FELP的分类准确率接近算法FWELL-EN,说明算法FELP的分类性能和算法FWELL-EN非常接近,证明了算法FELP的有效性。
3 结束语
在安全类机器学习中,具有隐私保护性能的特征选择是一个热门话题。文中提出了一种基于局部学习的带有输出干扰策略的差分隐私集成特征选择算法FELP,并且从理论上证明了该算法满足差分隐私,同时通过实验也证明在特定隐私度下,该算法是有效实用的。
