Spar型海上浮式风机极端载荷预报
2018-10-15王迎光李昕雪
周 帅,王迎光,李昕雪
(上海交通大学 船舶海洋与建筑工程学院,海洋工程国家重点实验室,高新船舶与深海开发装备协同创新中心,上海 200240)
0 引 言
为了保证海上风机的结构完整性,国际电工委员会在设计标准IEC 61400-3[1]中,对支撑结构和叶轮-机舱组合件的设计提出了极限强度分析的要求,其中设计载荷是分析中的必要参数,求解方法通常为IEC 61400-1[2]中介绍的基本方法,直接积分法。虽然直接积分法便于理解与扩展,但是由于算法本身的缺陷,当考虑的环境变量中不止有风还有波浪等时,所需的仿真次数也急剧增加,因此给海上风机极限载荷的求解造成了困难。
为了减少仿真数量,反向一阶可靠度法IFORM(Inverse First-Order Reliability Method)逐渐被运用到考虑多维变量时极限载荷的求解上。P.J. Moriarty等[3]曾采用直接积分法求解WP_Baselline1.5MW风机叶片根部面外弯矩在1年重现周期下的极端载荷,而Korn Saranyasoontorn等[4]采用2维IFORM法(环境等值线法)以更少的仿真数据便得到了同样良好的结果。K.Saranyasoontorn等[5]曾根据IFORM的3种形式建立了求解风机名义载荷的基本模型,求解了某600 kW陆上风机叶片的极端载荷;D. Karmakar等ADDIN EN.CITE.DATA[6–8]利用IFORM法求解了3种不同浮式基础NREL5MW海上风机的极限载荷,并对计算结果与浮式基础的关系进行比较;Puneet Agarwal等[9]在样本经验分布函数的基础上采用环境等值线法求取了工作在20 m浅水区域NREL5MW海上风机的长期载荷。
但是在上述研究中,一般都是等间距地在搜索区域上选取搜寻点,外推结果的精度由间隔搜寻角的大小直接决定,间隔角越小外推结果就越精准,但同时仿真数量也会增加。而采用IFORM求解极端载荷实际上也是一个最优化过程,因此本文将环境等值线法与1维最优化方法二分法结合起来,形成一种具有搜寻策略的算法来求解极端载荷,通过多级搜寻逐步缩小搜寻区间,减少不必要的搜寻工作,提高外推精度。同时与传统的直接积分法进行对比验证。
1 计算原理
1.1 IFORM原理简介
直接积分法的计算公式如下
而在“ 反向”的一(阶可)靠度问题中,事先已知的是可靠性指标,要求的变量是设计抗力,问题转化为如下形式
对比可知,在对结构进行可靠性分析中,搜寻的目标,即可靠性指标为标准正态空间内失效面上与坐标原点距离最近的点。而在求解设计抗力的问题中,搜寻的目标为标准正态空间内半径为的球面上短期载荷极值最大的点。
1.2 IFORM的3种形式
图 1(c)为IFORM法最基本的形式,即三维IFORM法。图 1(b)为IFORM法的二维简化形式。设为短期载荷极值分布的中位数,满足条件
2 数值算例
2.1 Spar型海上浮式风机
NREL海上5MW风机是美国国家可再生能源实验室(National Renewable Energy Laboratory)开发的一款风机[12],根据子结构和基础形式的不同分为多种类型。其中,OC3Hywind是一种Spar型浮式基础的海上风机,如图 2所示。基本参数见表 1。
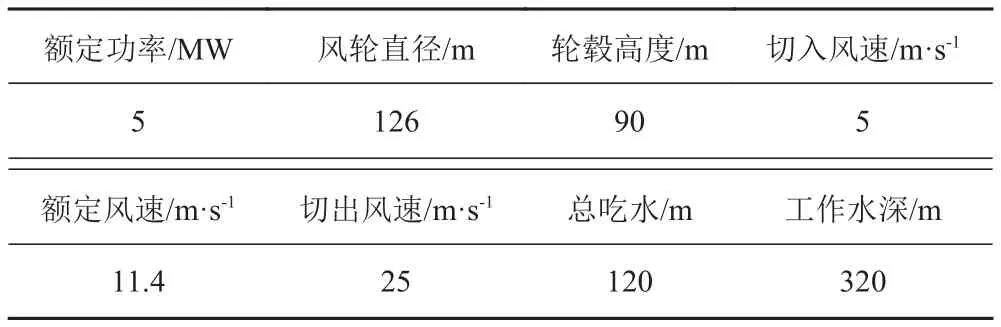
表 1 基本参数Tab. 1 Basic parameters
2.2 计算工况
计算工况以IEC 61400-3中正常发电工况的DLC 1.1为例,风机等级IECⅠ-A。参考Korn Saranyasoontorn等[13]中丹麦Horns Rev处的海洋气象条件,调整相应的参数使风机运行在一个较合理的环境下。假定平均风速服从韦伯分布
并且只考虑在工作风速区间内失效的情况,因此对切入风速以下和切出风速以上进行截断,将平均风速的实际分布函数改写为
假定有义波高服从正态分布。
对谱峰周期取值如下:
3 极限载荷求解
3.1 搜索算法
采用环境等值线法求解该风机1年重现周期和20年重现周期下的长期载荷,求解对象为叶片根部面外弯矩OOPB(Out-of Plane Blade Root Moment)以及塔筒基底首尾弯矩TBM(Fore-aft Tower Base Moment)。基本流程如图 3所示。
3.2 1年重现周期结果
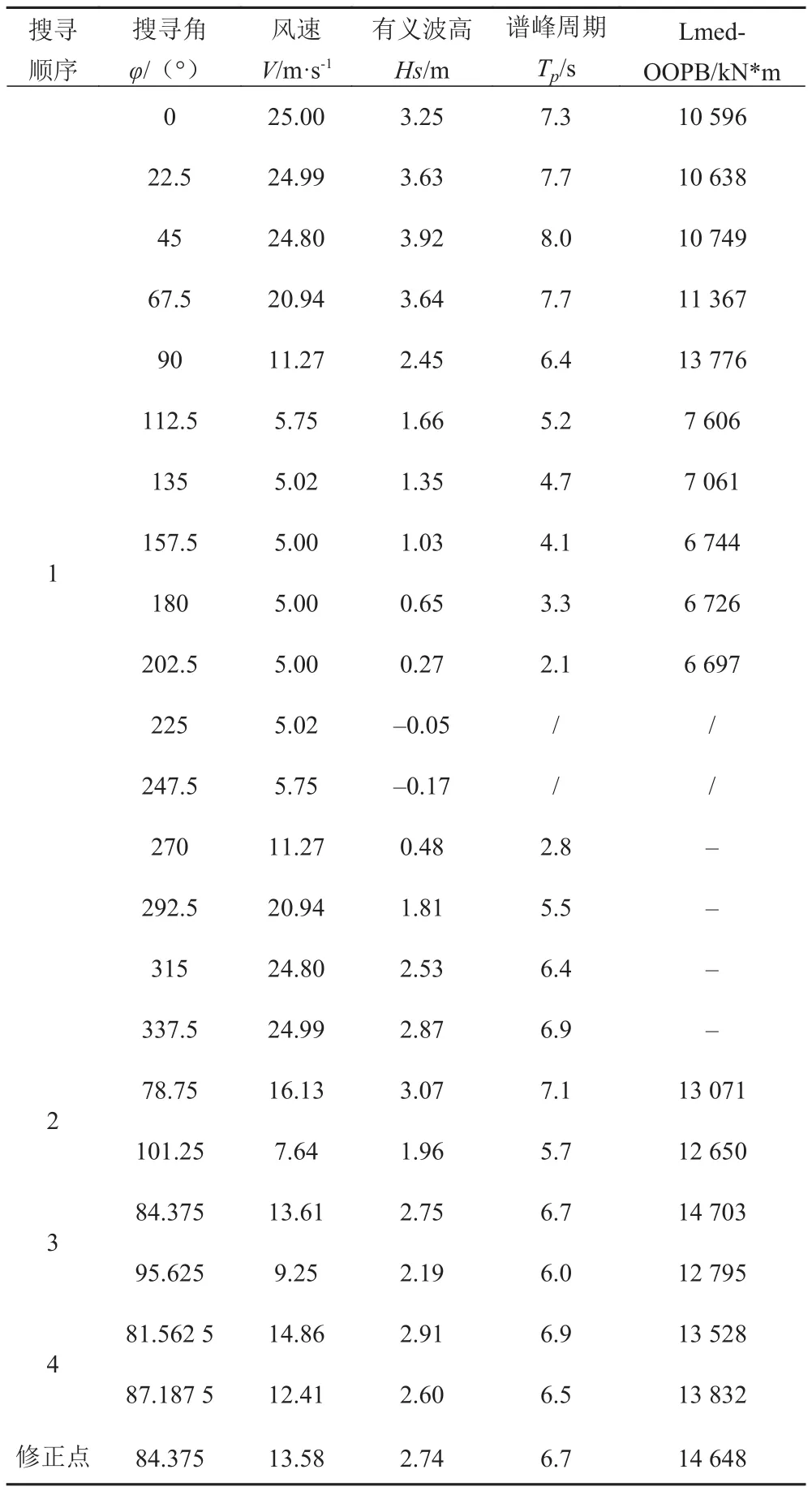
表 2 1年重现周期OOPB搜寻结果Tab. 2 Search results of OOPB in 1 year return period
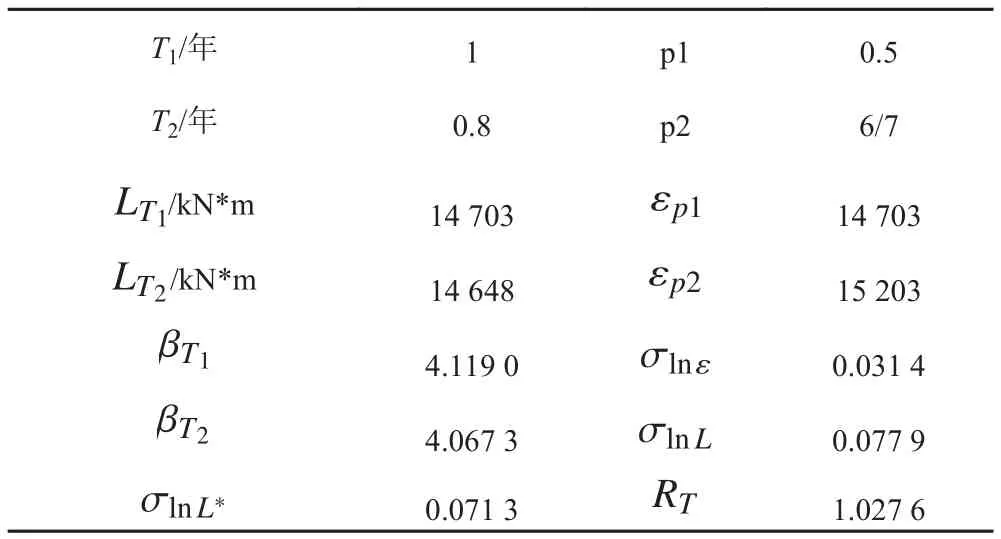
表 3 1年重现周期OOPB设计点修正Tab. 3 Correction of the OOPB design point in 1 year return period
由于计算中发现TBM短期极值的不确定性比OOPB更大,因此设定收敛条件为=2°。1年重现周期下TBM的极端载荷见表 4和表 5。
3.3 20年重现周期结果
为了之后与直接积分法进行更多的对比验证,同时还计算了20年重现周期时的极限载荷。搜寻过程与1年重现周期类似,在此不予赘述。最终获得20年重现周期下OOPB极限载荷为。20年重现周期下TBM极限载荷为
4 积分法对计算结果的验证
为了对比验证搜索算法的外推结果,根据式1采用直接积分法求解OOPB和TBM的长期分布。首先确定整个2重积分的积分域。根据前文定义的计算工况和平均风速的分布函数,取平均风速的积分区间为5 m/s~25 m/s;根据有义波高的分布函数取积分区间0 m~5 m。然后将各自的积分区间划分成多个子区间。为此将平均风速按照2 m/s的分辨率划分成11个子区间,各子区间平均风速为 5 m/s,7 m/s,···,25 m/s。将有义波高按照1 m的分辨率划分成5个子区间,各子区间平均有义波高分别为0.5 m,1.5 m,···,4.5 m。综上所述,总积分域被划分成55个子区间。

表 4 1年重现周期TBM搜寻结果Tab. 4 Search results of TBM in 1 year return period
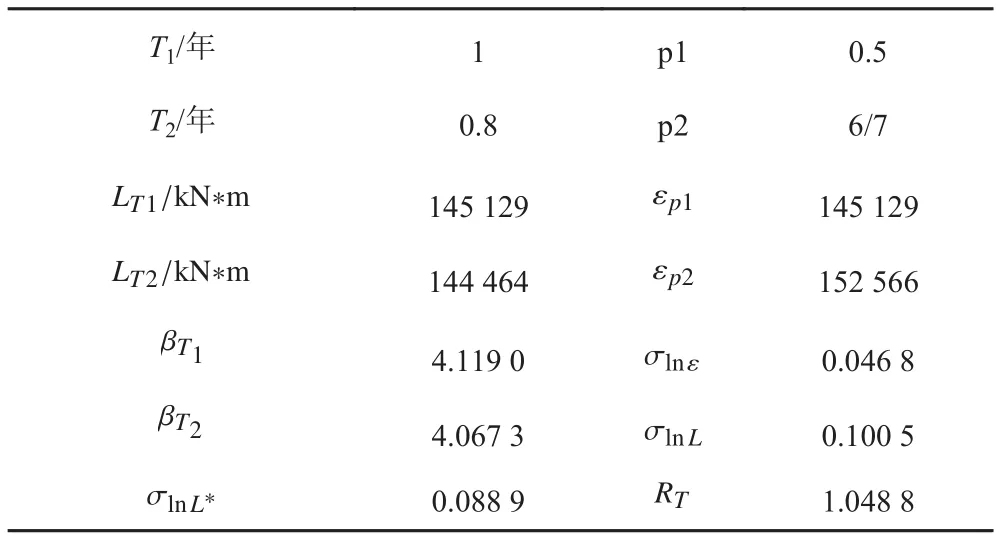
表 5 1年重现周期TBM设计点修正Tab. 5 Correction of the TBM design point in 1 year return period
确定好各子区间后根据其风浪参数,对风机在该环境条件下的运行进行数值仿真,以获取短期极值点。本文对每个风浪点均进行至少6次随机仿真。首先由湍流风软件TurbSim[14]产生湍流风数据,然后导入风机仿真软件FAST[15]进行10 min短期仿真,最后从输出结果中提取时域响应的极值点。采用常见的分块法选取极值点,根据夏一青等[16]的建议取分块数30,即从每次仿真中选取30个极值点。以平均风速13 m/s,有义波高4.5 m的某次随机仿真为例,选取OOPB短期极值点如图 6所示。
1年和20年重现周期下搜索算法与积分法的对比如表 6所示。其中OOPB1和TBM1为搜索算法直接搜寻的结果,OOPB2和TBM2为经修正点修正之后的结果。
由表中数据可见,在4项对比中,搜索算法预估的失效点与积分法预估的设计点均较一致,平均风速的误差不超过1 m/s,这表明搜索算法具有良好的识别能力,能够有效地分析出风机正常发电时最有可能出现失效的情况。
对于不确定性较小的叶片根部首尾弯矩OOPB,搜索算法外推结果与积分法更接近,修正因子的数值也更小。塔筒基底首尾弯矩TBM较OOPB的不确定性更大,在和积分法直接比较时,存在一定误差,并且重现周期越大误差也越明显。然而较大的不确定性也导致了较大的修正因子,所以在一定程度上弥补了搜索算法的不足。经过修正因子修正之后,外推结果与积分法更为接近,误差在5%左右。
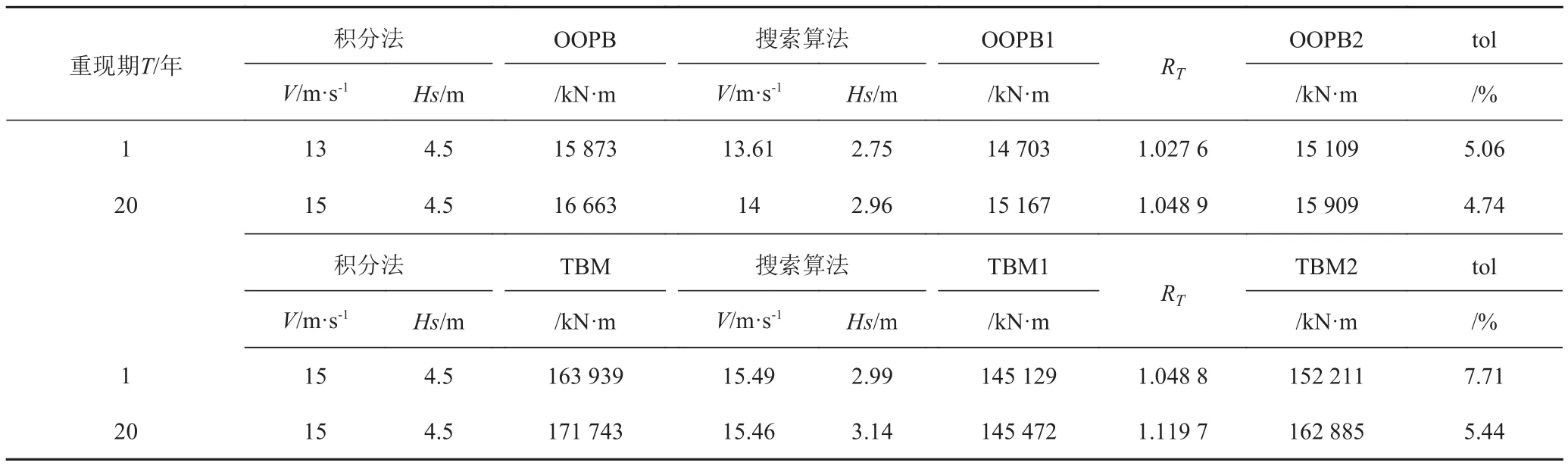
表 6 搜索算法与积分法外推结果对比Tab. 6 Comparison of extrapolation results of search method and integration method
5 结 语
将EC法与二分法结合起来形成一种新的搜索算法,应用于求解Spar型浮式风机叶片根部面外弯矩和塔筒基底首尾弯矩在1年和20年重现周期下的极端载荷,主要可得以下结论:
1)相较于积分法55组的仿真数量,搜索算法仅利用17~19组仿真便获得了相应的极限载荷与设计点,因此在计算成本上具有较大的优势。
2)经过与传统直接积分法的外推结果对比验证,发现在极限载荷数值和引发失效的设计点上均较一致,说明了搜索算法同时也具有较高的可靠性。
3)作为参考,EC法还可结合其他最优化方法以进一步减少仿真需要的数量,提高求解精度。
