基于粒子群算法优化核极限学习机的磨煤机故障诊断

2018-10-13张文涛马永光董子健杜景琦

电力科学与工程 2018年9期

张文涛，马永光，董子健，杜景琦

(1.华北电力大学控制与计算机工程学院，河北保定 071003；2.云南电力试验研究院(集团)有限公司，云南昆明 650217)

0 引言

磨煤机是火电厂制粉系统非常重要的设备，其工作状况对于整个火电机组的安全和经济运行具有非常重要的意义，一旦磨煤机发生故障，将会影响制粉系统的正常运行，其后果较为严重[1，2]。二十世纪八十年代之前，一般都是依靠人工分析和信号处理来对故障进行诊断和分析，这种方法效率低且准确率不高。随着人工智能技术的不断发展，许多机器学习方法开始运用到故障诊断之中。支持向量机(Support Vector Machine, SVM)是一种得到广泛应用的机器学习算法，文献[3]利用核主元分析(Kernel Principal Component Analysis, KPCA)提取特征向量，将提取后的主元作为SVM的输入，进行诊断和分类。此外，许多专家学者利用神经网络进行磨煤机的故障诊断。文献[4]使用RBF神经网络，但训练样本过大时，训练速度会很慢。文献[5]提出基于粗糙集(Rough Set, RS)和概率神经网络的故障诊断方法，解决了样本维数和训练速度的问题，但是粗糙集理论[6，7]对数值型数据进行离散化处理，会带来信息损失。随着信息融合技术的发展，许多基于D-S证据理论[8]的方法开始应用到磨煤机故障诊断中来，文献[9]将灰色关联分析与D-S证据理论相结合，文献[10]将模糊聚类分析与D-S证据理论结合，通过证据之间的相互融合，提高了故障诊断的准确率。

极限学习机(Extreme Learning Machine, ELM)是由南洋理工大学的黄广斌教授[11]在2006年提出的一种单隐含层前馈神经网络(Single-hidden Layer Feedforward Neural networks, SLFNs)的快速学习算法。ELM算法在学习过程中，无需调整网络的输入层与隐含层之间的权值和隐含层神经元的偏置，只需要设置隐含层节点的个数，就会产生唯一的最优解，与传统的BP神经网络相比，ELM训练速度快且泛化能力强。但是，对于某些分类或者回归问题，极限学习机往往需要较多的隐含层节点，且容易过拟合[12，13]。因此在此基础上，黄广斌又将核函数的思想引入到极限学习机中，提出了核极限学习机(Kernel Based Extreme Learning Machine, KELM)算法[14]。本文将KELM应用到磨煤机的故障诊断中，并且利用粒子群算法优化核极限学习机的参数，实验结果证明了本文方法的可行性和有效性。

1 核极限学习机

KELM借鉴了支持向量机[15]的思想，采用核函数来代替ELM隐含层节点的特征映射，与ELM相比，KELM无需人为确定隐含层节点的数目，只需要选择合适的核函数参数，就能得到输出权值。

给定N个训练样本数据集(xi,ti)，其中xi=[xi1,xi2,…,xin]T∈Rn为样本输入数据，ti=[ti1,ti2,…,tim]T∈Rm为样本输出值，对于有L个隐含层节点数的SLFNs，设其激励函数为g(x)，则其网络输出为：

(1)

式中：βi为第i个隐含层节点和输出层节点之间权值向量；ωi为第i个隐含层节点和输入层节点之间的权值向量；bi为第i个隐含层的偏置；yj为网络的输出值。

(2)

因此，上述N个方程可以表示为

Hβ=T

其中，

(3)

式中：H为隐含层输出矩阵；T为期望的输出向量。

通过最小二乘法确定网络的输出权值为：

β=H+T=HT(I/C+HHT)-1T

(4)

式中：H+为隐含层输出矩阵的Moore-Penrose广义逆矩阵；C表示惩罚因子。在矩阵HHT中加上I/C可以使其特征根偏离零，可以提高结果的稳定性和泛化能力。

对于KELM算法，输出函数的表达式如下：

f(x)=h(x)HT(1/C+HHT)-1T

(5)

定义核函数的计算式如下：

(6)

核函数的选择有很多种，本文选择RBF核函数，定义如下：

(7)

所以KELM的输出函数表达式为

(8)

式中：γ表示核函数参数。在KELM算法中并不需要知道隐含层节点的特征映射函数，只要知道核函数的具体形式，就可以求出输出函数的值。与传统的ELM相比，KELM无需设定隐含层节点数，也不用随机设定初始权值和偏置，因此具有更好的函数逼近能力和分类能力。

2 基于粒子群优化核极限学习机的参数优化算法

粒子群优化算法(Particle Swarm Optimization,PSO)是一种群体智能算法[16，17]，其基本思想是通过群体中个体对信息的共享从而使得整个群体的运动在求解空间中产生一种有序的演变，从而获得最优解。所有的粒子都具有一个位置向量和速度向量，并可以根据目标函数值计算当前的所在位置的适应值，在每次的迭代中，种群中的粒子通过自身的经验和种群中最优粒子的经验来学习，就这样逐步迭代，从而使得整个种群中的粒子趋于最优解。

令Xi=(xi1,xi2,…,xin)表示粒子的位置向量，Vi=(vi1,vi2,…,vin)表示粒子的速度向量，速度和位置更新公式如下：

(9)

(10)

式中：Pbest代表个体的局部最优位置；Gbest表示种群的全局最优位置；ω是惯性权重；c1、c2为学习因子；r1、r2为[0,1]之间的随机数。

惯性权值ω的调整公式如下：

ω=ωmax-t*(ωmax-ωmin)/tmax

(11)

式中：t表示当前迭代次数；tmax为最大迭代次数。

3 基于PSO-KELM的磨煤机故障诊断方法

火电厂运行环境复杂，而制粉系统磨煤机故障类别多，且难以通过故障征兆判断故障原因。KELM算法无需设置隐含层节点数，且训练时间短，分类精度高，具有非常好的泛化性能。由于KELM引入了核参数会导致对参数的非常敏感[18]，因此采用粒子群算法去优化核函数的参数γ和惩罚因子C[19，20]。基于PSO-KELM的磨煤机故障诊断方法的流程图如图1所示，具体步骤如下：

(1)将样本数据分为训练样本和测试样本。

(2)对数据进行归一化处理。

(3)初始化粒子群算法的参数，确定组合搜索参数[C,γ]的搜索范围。

(4)利用初始的惩罚系数C和核函数的参数γ，训练KELM。以样本的分类精度作为适应度函数，通过计算每个粒子的适应度值不断更新个体最优位置和群体最优位置。

(5)根据公式(9)、公式(10)和公式(11)，更新粒子的速度、位置和惯性权值。

(6)当适应度满足条件或者达到最大迭代次数时，终止优化过程，否则返回步骤(4)。

(7)根据寻优得到的最佳惩罚系数C和核函数的参数γ，建立KELM故障诊断模型。

(8)利用已经训练好的KELM故障诊断模型对测试样本数据进行故障诊断。

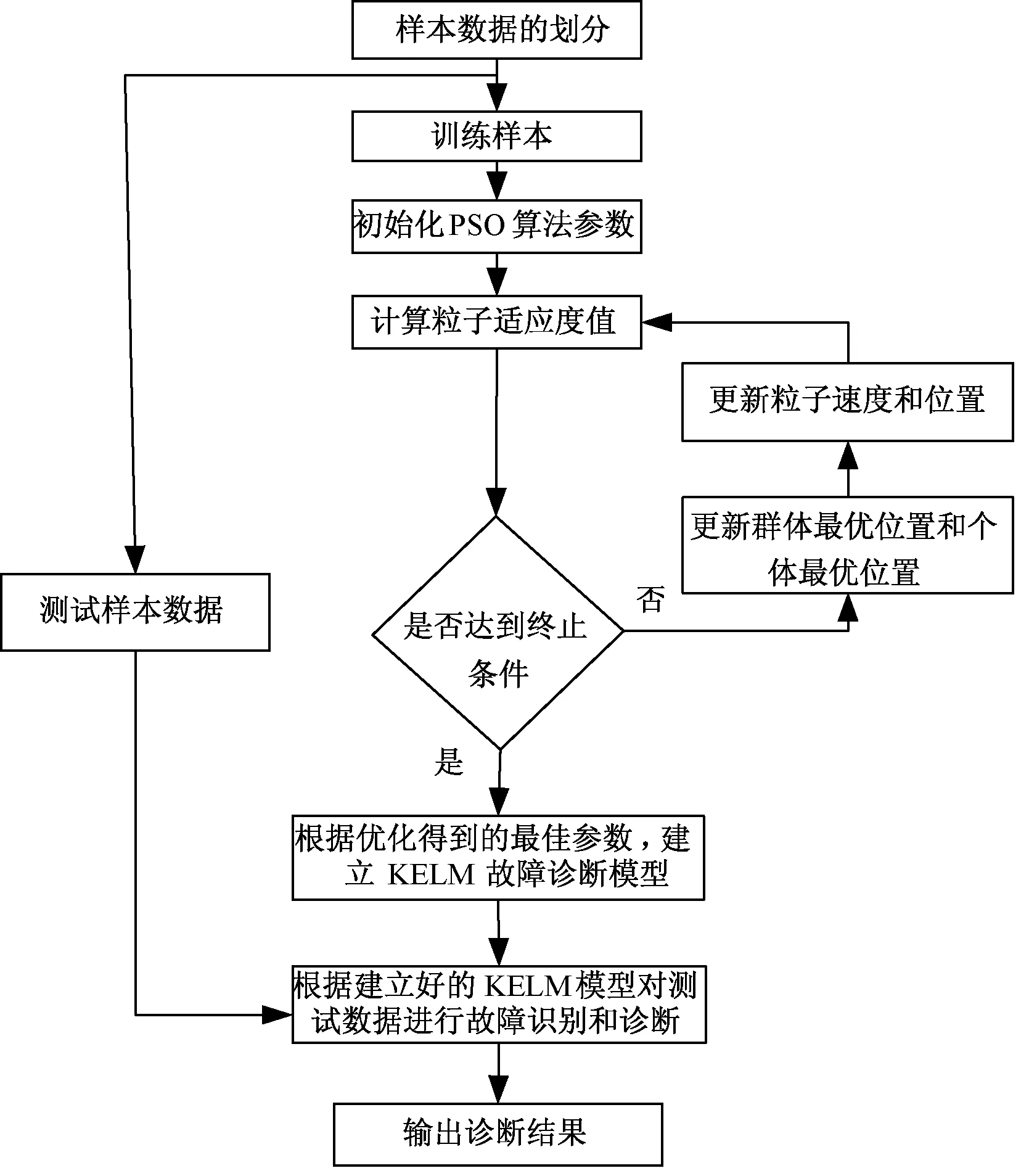
图1 基于PSO-KELM的磨煤机故障诊断流程图

4 实例分析

(1)样本的选取及处理

本文以正压直吹式中速磨煤机为研究对象，样本数据来自于云南某600 MW机组，根据专家知识和机组以往历史运行经验[21]，输入参数选择跟磨煤机相关的11个测点，分别为磨煤机电流、磨煤机齿轮箱推力瓦温度、磨煤机润滑油温度、磨煤机入口温度、磨煤机一次风流量、磨煤机入口压力、磨煤机进出口压差、磨煤机出口温度、磨密封风与一次风差压、分离器出口压力、给煤量。输出参数为4种状态，分别为正常状态、磨堵煤、磨断煤和煤粉自燃。一共选取160组数据，每类数据40组，数据进行归一化处理，消除量纲的影响，归一化公式如下：

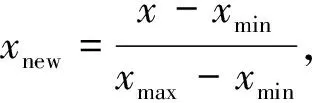
(2)模型参数的选择

本文选择PSO算法的参数如下：c1=c2=1.5，种群数量为20，最大迭代次数为100。经过粒子群算法优化KELM的参数，得到正则化参数最优值C=23.411，核参数γ=0.685。

(3)故障诊断

仿真实验一共有4类数据，其中每类数据40组，每类数据的前30组作为训练数据，建立KELM故障诊断模型，每类数据的后10组数据作为测试数据样本，一共有40个测试样本数据。建立KELM故障诊断，PSO-KELM模型在测试集上的故障诊断结果如图2所示。

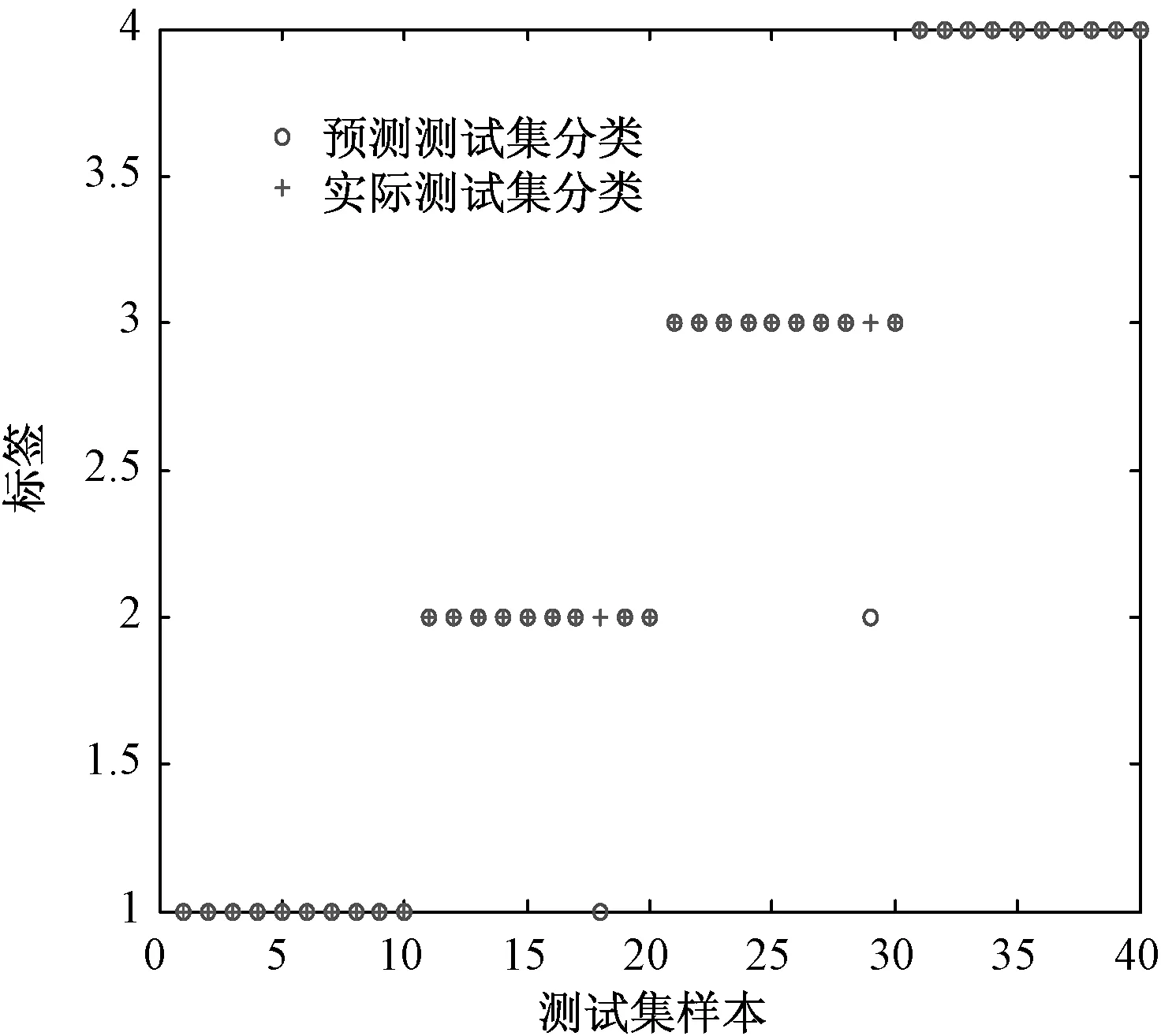
图2 测试集样本的故障诊断结果

从图2中可以看出，40个测试样本，只有2个诊断错误，故障诊断准确率可以达到95%。

为了进一步验证本文所提方法的优越性，再分别利用BP神经网络、SVM算法根据上文所示数据进行磨煤机的故障诊断。其中BP神经网络的输入层节点为11个，隐含层节点数为15个，输出对应4种状态。SVM采用RBF核函数，其中惩罚系数C和核函数的参数γ通过K折交叉验证得到，并且采用“一对一”的多分类方式。3种方法的训练时间和诊断准确率的比较如表1所示。

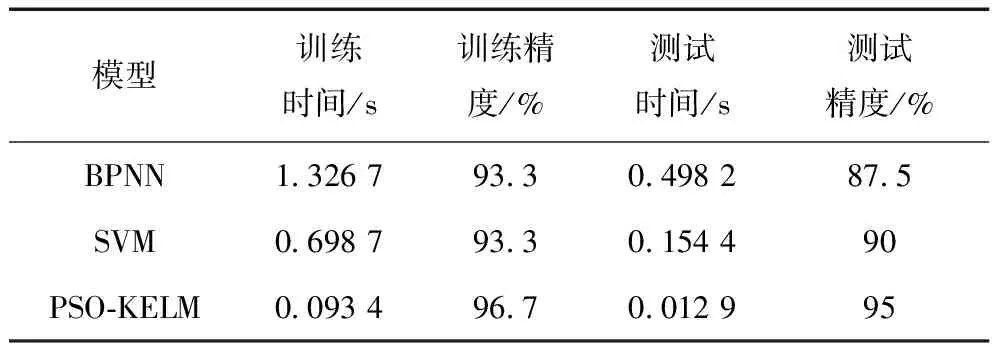
表1 诊断结果比较

从表1中可以看出，BP神经网络的训练时间和测试时间都是最长的且训练样本数据和测试样本的分类精度分别为93.3%和87.5%。基于SVM的磨煤机故障诊断方法要优于BP神经网络，在测试样本上的诊断准确率可以达到90%。但是很明显，文中所提的PSO-KELM方法的效果更好，训练时间只有0.093 4 s，且在训练样本上的准确率可以达到96.7%，在测试集上的诊断准确率可以达到95%。