一种基于ARMA模型的单回路控制性能评价方法

王印松， 苏婉婉， 高 颖， 蒋雄杰， 李士哲

(1. 华北电力大学 控制与计算机工程学院，河北 保定 071003；2. 浙江浙能嘉华发电有限公司，浙江 嘉兴 314000)

0 引言

工业过程中约90%的控制器都是PID控制器，其控制性能与产品质量、操作成本及生产安全都密切相关。在实际生产过程中，只有在调试阶段才会对PID控制器进行参数寻优，但是随着回路长时间的运行及现场工况的变化，控制系统性能退化，不能达到原先设计和整定时的性能。另外，一般的生产企业都有成千上百个控制回路，给维护工作带来了一定困难。因此，评估控制系统性能以确定控制器是否需要整定十分重要。然而常规控制器整定方法一般都需要整定参数后加阶跃响应，这样耗时耗力，不适合在线分析。因此利用在线性能评估方法来确定控制器是否需要整定和维护具有很重要的意义，只需要对评估结果较差的回路进行整定，大大减少了工作量。

对于PID控制器来说，控制器性能降低的原因可能来自控制器参数的调节问题、执行机构故障或干扰等。如何对由于控制器调节不当导致的性能降低进行参数优化，是控制系统性能评价的一个重要任务。Hägglund[1]通过分析控制量和被控量，定义了IDLE指标用于诊断控制回路响应迟缓情况；Visioli[2]基于控制量定义了面积指数，诊断回路对负载扰动的响应的突发性或缓慢性；Salsbury[3]基于输出数据响应峰的变化定义了R指数；Veronesi[4]首先估计了现有控制器的性能，然后在仅需要设定值改变的情况下完成控制器的参数调节。上述方法能够定量地判断控制器调节性能，但是需要在设定值或负载扰动出现大的阶跃变化的情况下使用，而工业现场中，这种情况较少，不适用于系统长期在线评价。针对现场中经常受到随机扰动的情况，Yamamoto[5]利用基于最小方差的PI系统性能评估结果对PI参数进行了在线优化控制；Goradia[6]提出一种基于系统脉冲响应曲线的方法判断当前控制器调节迟缓/振荡，通过迭代寻优的方法寻找PI控制器最佳性能。周猛飞[7]提出了一种基于双层结构PID控制器的性能评估方法，第一层是基于脉冲响应曲线和最小方差准则来评估控制器的确定性和随机性性能，接着对PID结构的控制器进行评估，该方法更符合生产实际，但需要更多的过程信息。吕书艳[8]将传统PID控制与模糊控制算法相结合，实现PID参数的在线整定。赵洪洲[9]等提出一种多指标性能评价方法，同时评价回路的响应和设定值跟踪情况、振荡情况及控制器的投用情况。孙超杰等[10]采用线性二次高斯(Linear Quadratic Gaussian, LQG)基准针对PID控制回路进行了性能评价分析，并给出最优控制器。

目前，基于脉冲响应曲线评价控制系统性能的方法有很多，但在工业实际过程中利用该方法评价当前控制器参数下系统响应迟缓/振荡的成果较少。本文利用系统单位脉冲响应函数与ARMA模型Green函数等价的特点[11]，通过对系统被控变量进行时间序列分析，得到系统单位脉冲响应曲线。根据脉冲响应曲线的性能分析系统克服随机干扰的能力，判断当前控制系统响应迟缓/振荡，同时给出控制器参数优化方向。在评价过程中，系统脉冲响应曲线方法与Harris指标[12]评价结果对比验证其有效性,同时在优化控制器参数过程中采用Harris指标作为结束标志。该方法只需要系统运行数据和迟延时间的信息，不会影响系统正常运行，适用于工业现场进行在线性能评价。

1 控制系统性能评价方法

1.1 脉冲响应曲线

脉冲响应曲线描述了噪声序列和系统输出之间的动态关系，可以直观地反映控制器调节随机干扰好坏的程度。不同于以往需要做设定值实验得到脉冲响应曲线，本文根据自回归滑动平均模型(Auto-Regressive and Moving Average, ARMA)Green函数即是系统单位脉冲响应的特性，通过对常规闭环运行数据进行时间序列分析即可获得系统单位脉冲响应函数。求解脉冲响应的步骤如下：

(1)建立ARMA模型。对采集数据进行预处理[13～15]，建立ARMA模型。由于扰动信号at未知，ARMA模型参数估计的过程中会出现非线性回归问题。而基于观测时序建立起来的自回归模型(Auto-regressive, AR)模型、ARMA模型是等价系统的数学模型，这两个模型在同一时刻的残差值at是相等的[16]。本文选用长自回归法[17，18]建立ARMA模型，即先估算AR模型后[19]根据传递函数相等的规则估计出ARMA模型。该方法能够避免ARMA模型参数估计中的非线性回归问题。

考虑典型的单输入单输出控制系统，其闭环过程通过ARMA模型表示，即被控变量与扰动变量之间的关系可以表示为：

(1)

式中：φ(B)=1-φ(1)B-…-φ(n)Bn；θ(B)=1-θ(1)B-…-φ(q)Bm，且φ(B)和θ(B)无公因式；B为后移算子。

(2)计算Green函数。上述ARMA模型也可用Green函数表示为[20]：

(2)

通过式(1)和式(2)可知

(3)

在ARMA模型参数φi、θi已知的情况下，通过比较式(3)两边B算子的同次幂系数即可知Green函数G(j)。

(3)系统单位脉冲响应。在ARMA模型建模中，at必须为白噪声，但模型建立后，参数φi、θi已经确定，从系统的观点来看，at可以是任意形式的输入，若式(2)的输入为单位脉冲，即at=δt-j，只有在j=t时，δt-j=1。则在j=t时，

X(t)=G(t)

(4)

可以看出，G(t)是系统对t时刻作用的单位脉冲所产生的响应，即系统单位脉冲响应函数y(t)=G(t)。

脉冲响应曲线可以直观地反映系统动态响应快慢及振荡等信息，如果脉冲响应曲线衰减很慢，则表明有较高的可预测扰动和相对较差的控制性能；如果是快速衰减的脉冲响应曲线，则表明该系统调节很好等。因此可以通过系统的单位脉冲响应曲线计算系统响应时间和振荡次数等，判断当前控制器调节下系统响应迟缓/振荡。

1.2 动态响应指标

因为系统单位脉冲响应函数是单位阶跃函数对时间的导数，可以证明单位脉冲响应曲线第一次过零点的时间就是单位阶跃响应曲线的峰值时间tp，即

y(tp)=0

(5)

另外，系统调节时间ts为系统单位脉冲响应曲线衰减到稳定值y(∞)的2%或5%的过渡过程时间，即当t≥ts时，

|y(t)-y(∞)|≤y(∞)*2%(或5%)

(6)

通过式(5)和式(6)可知，系统响应的第一次过零点时间tp和调节时间ts反映了系统响应速度。调节时间和峰值时间越小，系统响应的快速性越好。

此外，通过分析脉冲响应的振荡次数可以直观反映系统的相对稳定性。在过渡过程内，穿越稳态值的次数的一半即为振荡次数N，通过判断脉冲响应曲线穿越零点的次数即可求得振荡次数。振荡次数越多，说明系统调节过度，否则控制器调节较好或较为迟缓。

通过综合分析脉冲响应第一次过零点时间、调节时间和振荡次数来判断控制器调节迟缓/振荡，从而可以判断控制器调节方向，通过不断调整参数达到控制器最佳性能。

2 仿真验证

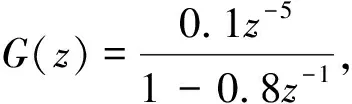
该过程采用PI控制器克服扰动，初始控制器的参数为：Kp=1.1，T=0.08。采集在该PI控制器作用下2 000个过程输出数据，采样时间为1 s。

根据上述性能评价方法，通过对过程输出数据建立ARMA模型得到初始控制器参数下闭环脉冲响应曲线，并根据评价结果对当前控制器参数进行逐步优化，具体参数优化过程如图1所示。

优化过程中系统脉冲响应曲线如图2所示，该过程初始控制器参数下的脉冲响应曲线如曲线a所示，其Harris指标为0.559 6。曲线b、c、d是不同参数下的脉冲响应曲线。

图1 脉冲响应曲线仿真优化结果

图2 系统仿真脉冲响应曲线图

可以看出脉冲响应曲线衰减缓慢，表明在该PI控制器作用下系统响应相对迟缓。因此，可以通过增大积分作用和比例作用加快系统响应速度。

从图1可以看出随着控制器参数的不断调整，脉冲响应曲线响应速度加快，且Harris指标也逐渐增大，表明控制器优化方向是正确的。

图1中Harris指标达到最大时为η=0.835 4，PI控制器参数为Kp=2.5，T=0.2，系统脉冲响应曲线如图2曲线c所示，其第一次过零点时间为10 s，调节时间为78 s，振荡次数为3，脉冲响应衰减速度较快且无较大振荡，系统调节性能较好。此时，若比例作用继续增大，如Kp=3，Harris指标η=0.786 5，脉冲响应曲线系统如图2曲线d所示，调节时间增大，振荡次数增加，系统性能明显降低；若比例作用减小，如Kp=2，Harris指标η=0.82，脉冲响应曲线系统如图2曲线b所示，第一次过零点时间增大，振荡次数减小，系统性能明显降低。因此，在Harris指标达到最大值时系统性能最佳，可以不用调整或进行细微调整达到需要的性能，与上述性能评价方法一致，该方法能够有效地调整控制器参数，优化系统性能。

3 现场数据分析

本文将上述性能评价方法应用到某电厂#1发电机组中，从2018年1月的常规操作数据中采集炉膛压力数据如图3所示(采样时间为5 s)，每两小时计算一次系统脉冲响应曲线和Harris指标，结果如图4所示。

图3 炉膛压力输出曲线

图4 炉膛压力脉冲响应曲线性能评价结果

可以看出，该系统脉冲响应曲线振荡次数较少，调节时间较短，即系统响应的快速性和相对稳定性较好，系统动态性能良好，相对应的Harris指标较好，因此控制器参数不需要重新调节。

采集2018年1月的系统正常运行状态的连排水位数据如图5所示(采样时间为5 s)，每两小时计算一次系统脉冲响应曲线和Harris指标，结果如图6所示。

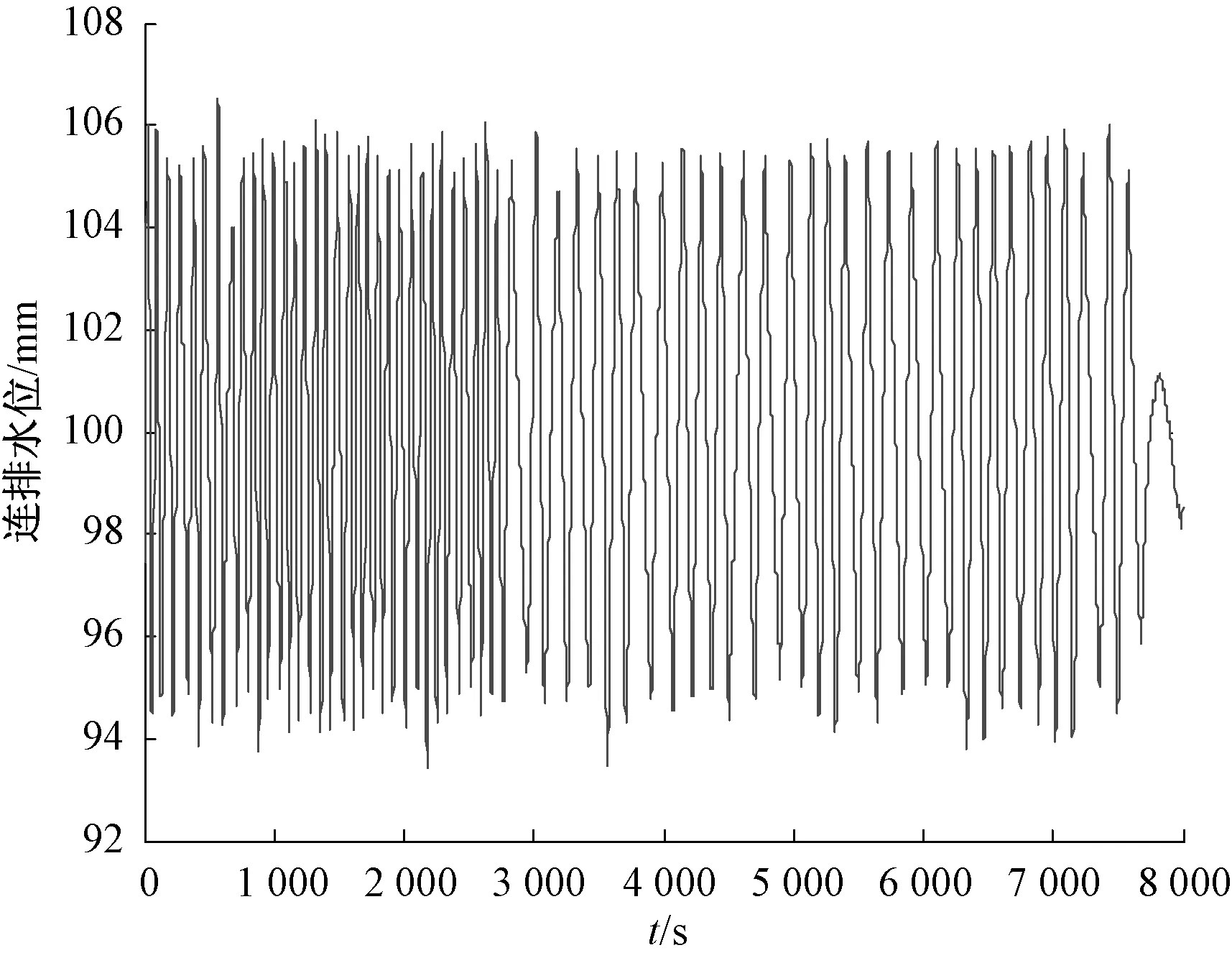
图5 连排水位输出曲线

图6 连排水位脉冲响应曲线性能评价结果

由图6可以看出，该系统脉冲响应曲线振荡较大，调节时间较长，即系统响应的快速性和相对稳定性较差，系统动态性能相对较差，对应的Harris指标都较差，可知当前系统性能距最佳性能还比较远，该PI控制器的控制性能还需要进一步提高。

采集2018年1月的系统正常运行状态的氢侧密封油温度数据如图7所示(采样时间为5 s)，每两小时计算一次系统脉冲响应曲线和Harris指标，结果如图8所示。

图7 氢侧密封油温度输出曲线

由图8可以看出，在12时和14时系统调节时间较长，Harris指标较差，可以判断在10时至14时时间段内该系统调节迟缓，但在之后的时间，系统响应的快速性和相对稳定性都较好，对应的Harris指标都较好。由于该系统某一段时间可能会出现调节迟缓的情况，控制器参数还没有达到最佳参数，该系统性能还能进一步提高。通过上述分析可以看出脉冲响应曲线法分析系统性能与Harris指标一致，因此该方法能够有效地对控制系统进行性能评价。另外，采用该方法能够很容易的分析当前系统响应速度并给出系统优化方向，且不需要对系统做任何扰动实验。

图8 氢侧密封油温度脉冲响应曲线性能评价结果

4 结论

本文研究了基于脉冲响应曲线的方法、针对单输入单输出控制系统进行性能评价，通过脉冲响应曲线对当前控制器调节下的响应快速性和平稳性进行分析，可以明确控制器参数优化方向，同时在仿真过程中利用Harris指标作为参数优化的结束标志，从而避免出现调节过度的情况。该方法仅利用闭环运行数据和系统延迟时间信息，不对系统的正常运行进行额外的任何形式的扰动，易于实现，适用于工业现场控制系统的性能优化。目前，该方法还有很多不足，首先，控制器参数可能需要调整几次才能达到最佳性能，但这是一个必须付出的代价，因为没有一个过程模型能够避免任何实验，仍然能够达到最高性能；其次，在本次工作中针对仿真回路做了性能优化研究，接下来可以针对实际工业系统进行性能优化实验。