积分分离模糊PID算法在MPPT中的应用

李宜伦，王胜辉，郑 洪,高 山，李锦秩.国网丹东供电公司，辽宁 丹东 8000)

随着煤、石油等传统化石能源的日渐缺乏，太阳能作为一种新型绿色可再生能源，具有储量大、经济、环保等优点而受到人们的广泛关注[1]。但是光伏电池在电能转换时很容易受到外界环境的影响(温度和光照强度)，不能一直保证电池的输出功率最大，所以保证电池最大功率输出,提高电池的转换效率显得尤为重要。

到目前为止，最大功率点跟踪的控制方法基本分为非智能控制和智能控制[2]。目前应用广泛的非智能控制方法为恒压法、电导增量法、扰动观察法，但是由于没有精确的数学模型，使得在寻优过程中出现了振荡、误判，造成了能量的损失。而智能控制算法则弥补了这个缺陷，模糊控制、神经网络等智能控制不需要精准的数学模型，但这些算法往往局限于跟踪速度和稳定程度的单一优化，难以将速度和稳定相互同时优化，无法去除两者之间的制约[3]。

本文首先建立了光伏电池和升压斩波电路的数学模型；其次对模糊控制、PID控制进行了分析，在此基础上首次将模糊控制与PID算法进行了结合并将其进行改进，引入了积分分离的概念，通过设置分离系数，将模糊PID控制器的工作模式分为模糊PD控制、半模糊PID控制和完整模糊PID控制，以寻优速度和稳定性为目标给出了具体的算法流程图以及控制器的结构框图，介绍了控制器的结构以及参数的选择，最后通过Matlab/Simulink仿真验证积分分离的模糊PID控制的优越性。

1 光伏电池组间模型

组成光伏电池的基本材料是半导体材料[4]，其等效模型即为1个恒电流源与1个二极管并联，并有1个串联电阻和并联电阻，文献[5]给出了其等效数学模型:

(1)

(2)

式中：I为光伏电池输出电流；V为光伏电池输出电压；ILG为光生电流；IOS为反向饱和电流；Id为二极管节点电流；q为单位电荷；T为电池板温度；A为理想因子；K为玻尔兹曼常数；RS为等效串联电阻；Rsh为并联电阻。

如图1、图2所示为光伏电池温度在25 ℃时，改变光照强度后的功率输出特性和伏安输出特性，外界环境(温度、光照强度)对太阳电池的功率输出有很大影响，保证光伏电池在快速到达并运行在最大功率点(MPP)是提高转换效率的关键。

图1 伏安特性曲线

图2 功率特性曲线

2 系统构成

光伏系统结构如图3所示，本文DC-DC电路选择为Boost升压电路，Boost控制相对简单，结构也并不复杂，同时电路转换效率也相对较高。光伏电池并联1个滤波电容CPV，滤波电容是为了滤除电路输入电压波动。其控制过程为MPPT控制器通过采集信号继而生成1个占空比的PWM信号以此来控制IGBT的开通和关断。其负载电压Vload与光伏组间之间的电压Vpv之间的关系[6]：

(3)

等效电阻Req与负载电阻Rload之间的关系为

(4)

MPPT控制的实质就是通过改变IGBT的关断来产生占空比信号D，以此来改变外电路中等效电阻的大小，当等效电阻与内阻相同时系统就运行到了最大功率点。

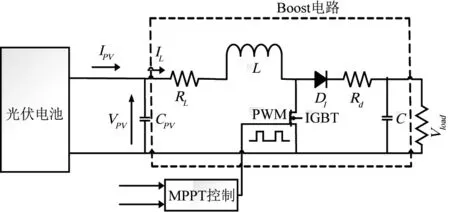
图3 光伏系统结构

3 单一MPPT算法

3.1 模糊控制算法

光伏MPPT控制的实质就是通过调节DC-DC电路的占空比使得负载与电池内阻大小相同使光伏电池功率达到MPPT点，本文MPPT的模糊控制器采用的是双输入，单输出[7]，其中：

Δe(k)=e(k)-e(k-1)

输出：调节步长

本文采用的是二维控制，取采样值的偏差量和变化率作为输入，将输入量进行模糊化处理，映射成为模糊论域内的某个值，得到可以用模糊集合和隶属度来描述的模糊变量，用编辑好的模糊控制规则对其进行判断，最后通过解模糊化处理得到系统的扰动量，完成对整个系统的控制[8]。

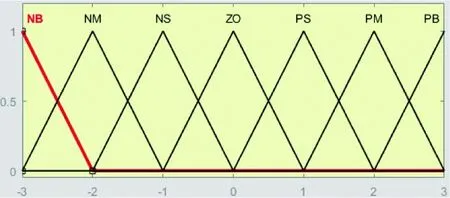
本文选用mamdani模型作为模糊控制方法，选择“交”方法为min，“并”方法为max，推理方法为min，聚类方法为max，解模糊方法为重心法[9]。输入量e和输出量ΔD分别定义为8个和6个模糊子集，输入和输出的隶属度函数如图4所示，光伏电池随着两端电压的增大，电流逐渐减少，在最大功率点左侧，功率逐渐增大，Ppv(k)-Ppv(k-1)>0，Ipv(k)-Ipv(k-1)<0，所以此刻e(k)<0，还可知，随着逐渐靠近最大功率点，Ppv(k)-Ppv(k-1)逐渐增大，Ipv(k)-Ipv(k-1)逐渐减少，得到Δe(k)的变化规律，将其转变为控制规则，如图4所示。

(a)输入隶属度函数

(b)输出隶属度函数图4 隶属度函数

但是该控制方法仍旧具备一定的局限性，文献[10]说明模糊控制存在固有的精度死区,模糊规则制定和变量、参数的设置需要依赖专家的经验和变量、参数的设定，而且由于缺少积分项I的控制作用，很难消除其静态误差[11-12]。

3.2 PID控制法

PID控制的基本组成为PID控制器和控制函数。其中比例系数P的作用是按照一定的比例反映系统的误差，当系统出现偏差时P就会进行调节减少误差；积分系数I的作用是消除静态误差，过大的I值使系统稳定性下降，动态性能减慢；微分系数D调节系统偏差变化率，具有预见性，能产生超前控制作用。其控制过程为当系统出现偏差时它根据设定的r(t)和实际的输出值y(t)构成1个控制的偏差量，继而将偏差量按比例、积分、微分通过线性组合成为1个控制量u(t)对控制函数进行控制[13]。其离散函数、传递函数表达式分别为[14]

(5)

(6)

PID控制器其结构简单，稳定性良好，但是由于其非线性、时滞性的特点很难建立被控对象的精确数学模型，所以PID控制的适应能力弱且控制力低。

4 积分分离的模糊PID控制

4.1 工作原理

模糊控制中由于缺少了积分模块使得系统会出现静态误差；PID控制中没有精确的数学模型，参数的设定需要大量的人为试验，这就大大影响了运行结果的准确性，缺少良好的鲁棒性和稳定性；将模糊控制算法与PID算法结合，既消除了静态误差影响，又不需要具体的数学模型，但是模糊PID控制算法中积分项I一直起到控制作用，虽然消除了模糊控制中静态误差的影响，但是降低了系统的动态性能，对此本文设计了一种积分分离的模糊PID控制器，其该方法结合了模糊控制和PID控制的优点，消除了模糊控制中静态误差的影响，控制积分项的大小使系统不会出现过大的超调，同时也不需要依赖完整的数学模型。其主要由1个模糊控制器和1个PID控制器组成的1个闭环控制，通过分离系数的选取对PID控制器中积分项I进行控制，使输出模式分为3种：完整模糊PID控制、半模糊PID控制、模糊PD控制。完整积分分离模糊PID控制器的传递函数：

(7)

式中：α为分离系数，判定对象为上文提到的e(k)，经过多次的试验调整，本文中α的具体取值为

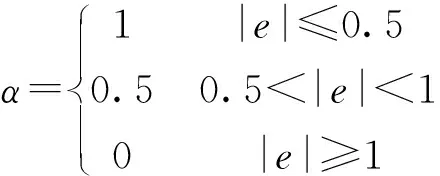
当|e|≥1时，PID控制器中的积分项不起作用，此时采用的是模糊PD控制，避免了系统由于积分积累而使系统无法退出饱和输出状态，缩短了系统响应的时间；当0.5<|e|<1时，采用的是半模糊PID控制，这是为了避免由PD转换为PID控制时，产生较大的振荡；当|e|≤0.5时，控制器采用的是完整模糊PID控制，缩短了系统寻优时间，提升了系统性能，运行过程如图5所示。

图5 积分分离的模糊PID控制结构

4.2 控制器的设计

4.2.1 控制器的结构设计

积分分离模糊PID控制器其控制结构设计主要是由模糊控制模块、PID控制模块和分离系数判定模块组成，输入信号e(k)进入模糊控制器后，输出为3个PID控制器的输入，并通过分离系数判定I的值，最后进入PID控制器，输出占空比信号。

4.2.2 控制器参数的设计

模糊控制器在设计时输入为

Δe(k)=e(k)-e(k-1)

输出：PID控制器3个增益量

输入为实际误差e和误差速度ec对应的模糊变量为E、EC，输出为PID控制器的3个增益量，模糊控制器输入和输出都选取为7个模糊子集[16]，分别为模糊子集{NB(负大)NM(负中)NS(负小)ZO(零)ZS(正小)ZM(正中)ZB(正大)}。其中ΔKp为比例增益量，ΔKi为积分增益量，ΔKd为微分增益量。PID控制器输入为Kp、Ki、Kd，各个控制参数可以表示为

(8)

式中：Kp0、Ki0、Kd0为PID控制器的初始值，是常量，本文中取值为300、0.3、280；ΔKp、ΔKi、ΔKd分别为各自的增益系数，是模糊控制模块的输出量；Kp1、Ki1、Kd1是增益因子[15]。其中增益系数是模糊控制模块的输出量，通过模糊控制对PID的参数进行整定，增强了该方法的鲁棒性和适应性[15]。控制过程中将变量归一化，归一化后的论域为[-1,1]，通过系统实际运行的动态范围，确定了模糊控制量化因子Ke、Kec和PID控制增益因子Kp1、Ki1、Kd1输入和输出变量变换的公式为式(9)所示(由于输出增益因子太多，这里只选取1个，其余依次类推)：

(9)

量化因子大小为0.3、0.1；增益因子大小分别为300、0.3、280，模糊论域均为{-3 3}其隶属函数均选为三角形分布输入输出形式如图6所示，为了更加具体的体现输入和输出之间的关系，制订了控制规则，其控制规则共有7×7=49条，为图7的if-then语句，输入ec、e对应的为输出ΔKp/ΔKi/ΔKd,，描述为

ife=Ajandec=BithenΔKp=Ci,ΔKi=Ci,ΔKd=Ci。

(a)输入隶属度函数

(b)输出隶属度函数图6 隶属度函数

图7 模糊控制规则

5 仿真结果分析

本文中光伏电池的基本参数均为Im=4.72 A、Um=18 V、Isc=5 A、Uoc=22.1 V，DC-DC变化电路采用的是BOOST升压电路，开关频率为10 kHz，温度在25 ℃，分别从静态和动态两个方面分析其功率特性。

5.1 静态特性分析

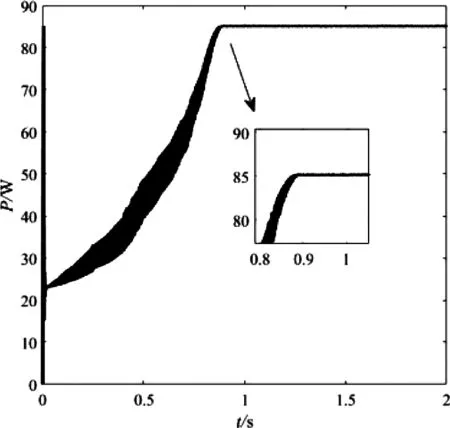
光照强度为1 000 W/m2，分别采用模糊控制、PID控制、模糊PID控制和基于积分分离的模糊PID控制对其静态特性进行仿真，仿真结果如图8所示，其数值结果为方法1系统在t=0.03 s进入最大功率点后，系统进入振荡，振荡范围83.28～84.38 W；方法2在t=0.85 s系统进入振荡，振荡范围为82.8～84.8 W；方法3在t=0.028 s系统到达最优值点P=85.8 W；方法4在t=6.39×10-4s系统到达最优值点P=84.96 W，静态结果可以看出PID控制对于控制函数精度要求较高，I+PD控制跟模糊控制算法结合后整体提升了输出功率的稳定性，明显缩短了初次寻优的时间，很好地平衡了速度和稳定精度的矛盾。

5.2 动态特性分析

分别采用模糊PID算法和积分分离的模糊PID算法对其进行仿真，其仿真结果如图9所示，其中光照1为800 W/m2、光照2为600 W/m2、光照3为1 000 W/m2，对比可以发现，积分分离的模糊PID与模糊PID在跟踪精度上均有误差，但其均可以快速跟踪到最大功率点且误差值均小于0.05%；在寻优时间上模糊控制PID 3次寻优时间分别近似为t1=0.023 s、t2=0.02 s、t3=0.024 s，积分分离模糊PID控制3次寻优时间分别近似为t1=5.8×10-4s，t2=6.2×10-4s，t3=3.8×10-4s，从结果可以明显看出积分分离模糊PID算法由于对积分项I进行了动态调节提高了系统的动态特性，其仿真时间明显短于模糊PID控制。

(a)模糊控制进行MPPT

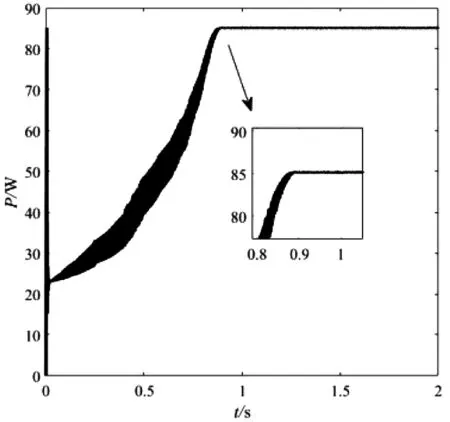
(b)PID控制进行MPPT

(c)混合算法进行MPPT图8 静态变化功率输出曲线

(a)模糊PID控制

(b)积分分离模糊PID控制图9 动态变化功率曲线

6 结束语

本文将I+PD控制和模糊控制相结合，完成了模糊控制算法的优化，通过对积分项I进行动态控制，通过分离系数去进行选择切换3种工作模式(模糊PD控制、半模糊PID控制、完整模糊PID控制)进行光伏电池的最大功率跟踪提升了系统的寻优的速度和稳定性，通过了Matlab/Simulink的验证。仿真结果表明基于积分分离的模糊PID控制具有非常良好的跟踪性能，符合寻优时间短、稳定性高的预期结果，有良好的控制性能。