基于动态弹性力学模型的煤系致密砂岩储层裂缝预测方法

黄玉欣，胡望水，尹 帅

(1.长江大学地球科学学院，湖北武汉 430100；2.中国石油吉林油田分公司勘探开发研究院，吉林松原138000；3.西安石油大学地球科学与工程学院，陕西西安 710065)

煤系致密砂岩储层具有岩性变化快、单层厚度小、非均质性强的特征，裂缝发育特征复杂。利用常规测井曲线无法直接对裂缝进行有效识别。裂缝的形成受控于岩石的弹性性质，且前人的研究表明[1_6]，裂缝在岩石部分声学参数或动态弹性参数上有良好的响应。因此，利用弹性力学模型对致密砂岩储层进行裂缝预测具有现实意义。目前，国内外基于动态弹性力学模型识别岩石裂缝的研究主要还停留在试验分析层面。同时，将动态弹性力学模型扩展到测井评价中的研究尚未进行。因此，基于高分辨率测井资料和动态弹性力学模型对单井裂缝进行定量表征，并从平面上标定出裂缝发育区，能极大地扩展该模型的应用范围。

微分等效介质(differential equivalent medium，DEM)模型是一类基于动态弹性力学理论的经典模型，侧重于定量表征具有不同形态孔缝结构弹性介质的动态力学性质[2]。该模型假设孔隙和裂缝的密度及方向均是随机分布的[3]，适用于具有强非均质性的致密砂岩储层。DEM模型通过定义岩石孔隙纵横比(α)，对岩石体积模量和剪切模量的常微分方程进行解耦，进而实现对含有不同孔缝岩石弹性性质的评价[4]。因此，笔者利用动态弹性力学模型对沁水盆地南部下二叠统山西组致密砂岩储层的裂缝进行了预测，预测结果与岩心裂缝观察结果一致。

1 DEM模型评价裂缝的原理

岩石的弹性性质取决于其矿物含量及分布、孔缝的数量及分布。目前，从微观尺度对岩石动态弹性性质进行评价的理论主要有有效介质理论和孔弹性理论2种。有效介质理论假设岩石内部的孔隙和裂缝是相对独立的，孔缝之间的连通性较差，而孔弹性理论假设岩石内部孔缝之间具有较好的连通性。J.G.Berryman等人[2]在上述理论研究的基础上，提出了DEM模型,其主要用于解决含裂缝介质的弹性问题。利用有限差分法求解DEM模型获取岩石孔隙纵横比α的研究，已经取得不少研究成果[1_4]。

DEM模型认为裂缝会对岩石的动态弹性性质产生显著影响。干岩石骨架模量与岩石基质矿物模量、孔隙度及孔隙纵横比α密切相关[4]。α为岩石椭球状孔隙短轴与长轴的比。根据α的值可将岩石孔缝形态分为球形孔(α>0.9)、针形孔(0.1<α≤0.9)、硬币形裂缝(0.01<α≤0.1)及无限狭长裂缝(α≤0.01)4类[7]。球形孔一般用来表征溶蚀洞，针形孔可用来表征溶蚀孔，无限狭长裂缝可用来表征裂缝。笔者对Berryman提出的耦合常微分方程进行解耦来求取岩石的α。Berryman提出的耦合常微分方程为[2]：

(1)

式中：φ为孔隙度；Ki和Gi分别为孔隙内成分或包裹体的体积模量和剪切模量，GPa；K*和G*分别为考虑基质矿物及孔隙组分的等效体积模量和等效剪切模量，GPa；P*i和Q*i分别为等效体积模量和等效剪切模量的激化因子。

对式(1)进行解耦，可得到干岩石骨架模量比Kd/Gd的计算公式[8]：

(2)

式中：Kd和Ko分别为干岩石和基质矿物的体积模量，GPa；Gd和Go分别为干岩石和基质矿物的剪切模量，GPa。

对阵列声波测井数据进行处理，可获取岩石的Kd，Gd，Ko和Go等模量参数，具体方法见文献[9_10]。各模量参数计算结果的可靠性可根据由Gassmann方程[9]预测岩石纵横波波速与实测纵横波波速的误差进行判定。m和n为式(3)的截距和斜率，两者均为α的函数。

(3)

采用线性方法对式(3)中的P*i-Q*i进行一阶求导[8]，即可确定n和m。

n=(P*i-Q*i)′

(4)

(5)

式中：P*i-Q*i和P*i-Q*i′的具体表达式见文献[8]。

基于寻优算法[11]对式(2)中隐含在m和n内的α进行反演。寻优算法是目前在提取干岩石模量及基质矿物模量方面较为成熟且最为常用的算法，所求取的结果与地层实际地质情况的相符度较高[11]。其主要思路是在合理取值范围内，对不同岩性地层岩石的基质矿物及骨架模量赋值，利用Gassmann方程反演岩石的纵横波波速，判断反演结果与测井测得的岩石纵横波波速的误差是否在允许误差范围内，如不在允许误差范围内，则调整各模量赋值，直至误差在允许误差范围内，此时各模量的值为最优解。当根据给定的α值所求取的Kd/Gd与利用阵列声波测井资料计算结果的误差达到允许误差时，此时的α值即为反演的目标值。

笔者反演岩石孔隙纵横比的技术路线如图1所示。首先迭代干岩石泊松比(νd)和Ko，基于Gassman-Biot-Geertsma等方程[11]对参数进行优化，最终求取地层岩石的α，并利用测井资料评价裂缝。

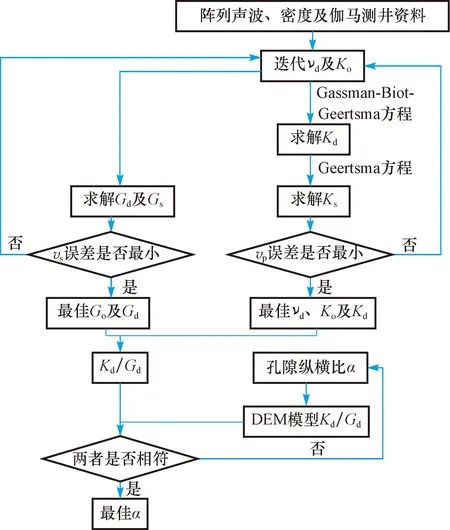
图1 岩石孔隙纵横波反演技术路线Fig.1 Technical route of rock pore P-S wave inversion

2 裂缝测井评价结果

2.1 模量参数的提取

研究区位于沁水盆地南部地区，属于残留型盆地，上古生界地层高角度走滑断裂极为发育，喜马拉雅期发生了大规模的隆升剥蚀等后期强烈改造作用[11]。研究目的层为下二叠统山西组煤系致密砂岩储层。

以研究区HG17_2井为例，利用寻优算法提取山西组煤系致密砂岩储层岩石的模量参数，结果如图2所示。该井491.00～512.00 m井段为煤系碎屑岩地层，512.00～520.00 m井段为煤岩地层。从图2可以看出，预测纵横波波速与实测纵横波波速的平均相对误差分别为4.00%和2.83%，因此各模量参数提取结果可靠。

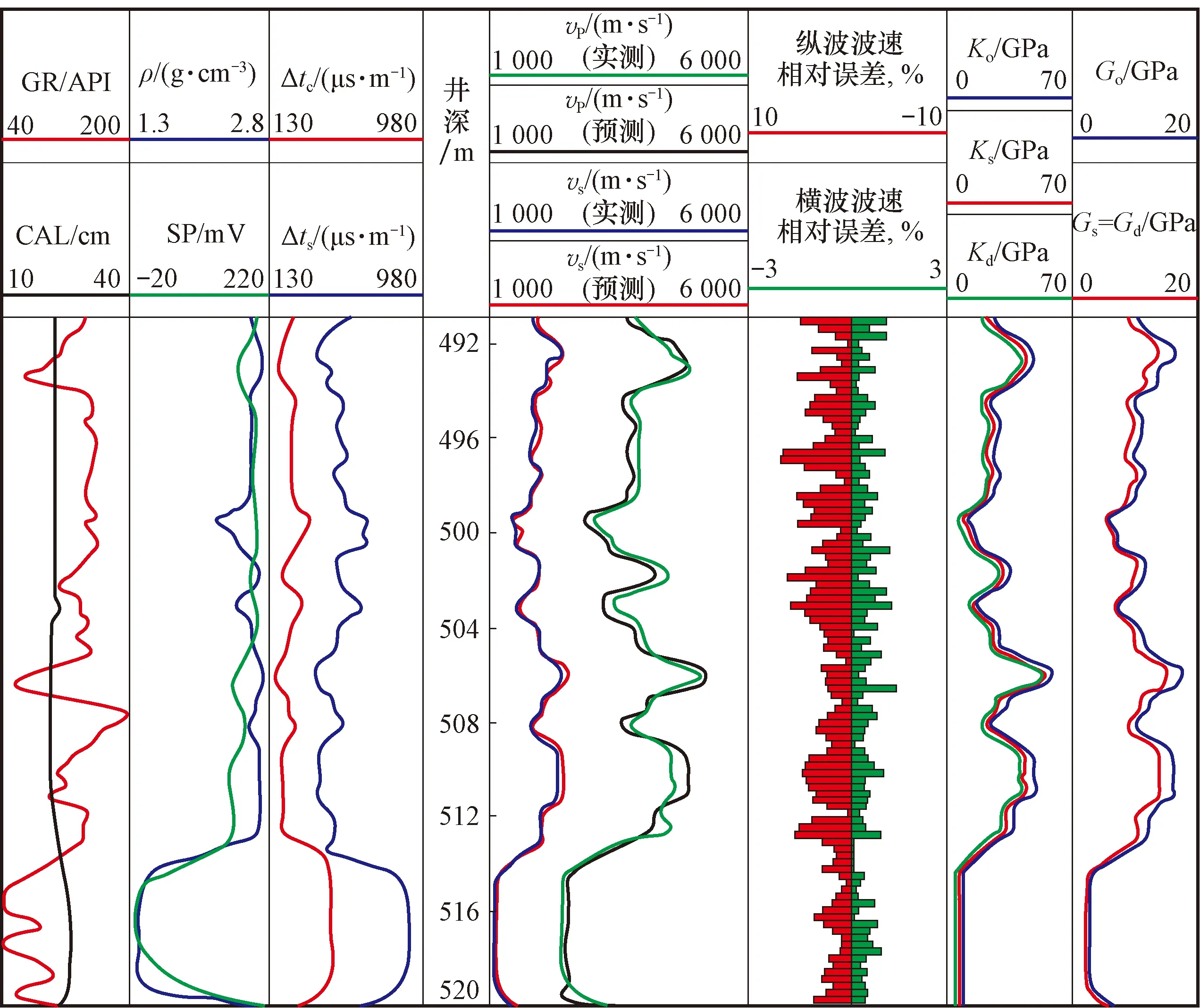
图2 基于寻优算法提取的HG17_2井各模量参数Fig.2 Various modulus parameters of well HG17-2 based on the optimization algorithm method 注：GR为自然伽马；CAL为井径；SP为自然电位；Δtc和Δts分别为阵列测井的地层岩石纵波时差和横波时差；vp和vs分别为纵波速度和横波速度；Ks和Gs分别为计算的地层岩石体积模量和剪切模量。

2.2 DEM模型测井解释

在提取了目的层各模量参数后，利用DEM模型求取了地层岩石的α。对利用寻优算法所提取的岩石Kd/Gd与式(2)的计算结果进行了对比，两者相符度较高(见图3)，表明利用式(2)所求取的α可靠。由图3可以看出：砂岩的Kd/Gd相对高一些，通常大于2.5，峰值约为3.3；泥岩次之，Kd/Gd主要分布在1.0～3.3，峰值约为2.4；煤岩的KdGd相对较小，通常小于1.8，峰值约为1.6。

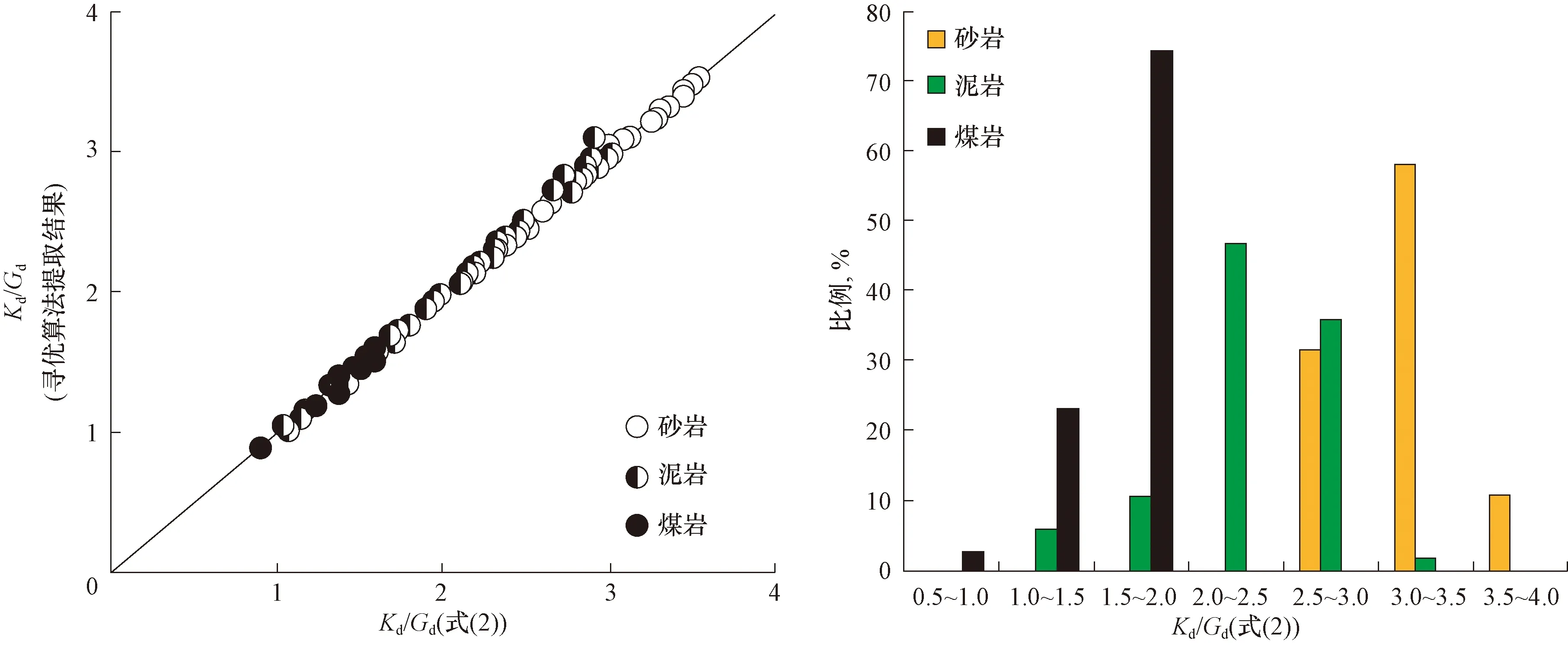
图3 HG17_2井山西组地层Kd/Gd计算结果与寻优算法提取结果对比Fig.3 Comparison of the calculated results and the extracted results of Kd/Gd of Shanxi Formation of Well HG17-2 based on the optimization algorithm method

2.3 裂缝测井预测

利用DEM模型对均匀分布在研究区的50口井的山西组地层的α进行了预测，部分井的预测结果见图4。从图4可以看出：利用该方法预测的裂缝发育程度与岩心裂缝观察结果基本一致，两者的符合率约达到90%，表明该方法适用于预测研究区煤系致密砂岩储层的裂缝；对于α小于0.1的裂缝性地层，砂岩段所占比例较高，表明裂缝主要在砂岩中发育，而泥岩地层则具有较好的封闭能力；裂缝性地层的α通常小于0.001，表现为无限狭长裂缝形态，表明裂缝延伸较长或具有较小的开度，这与显微镜下所观察到山西组岩心裂缝形态是一致的。

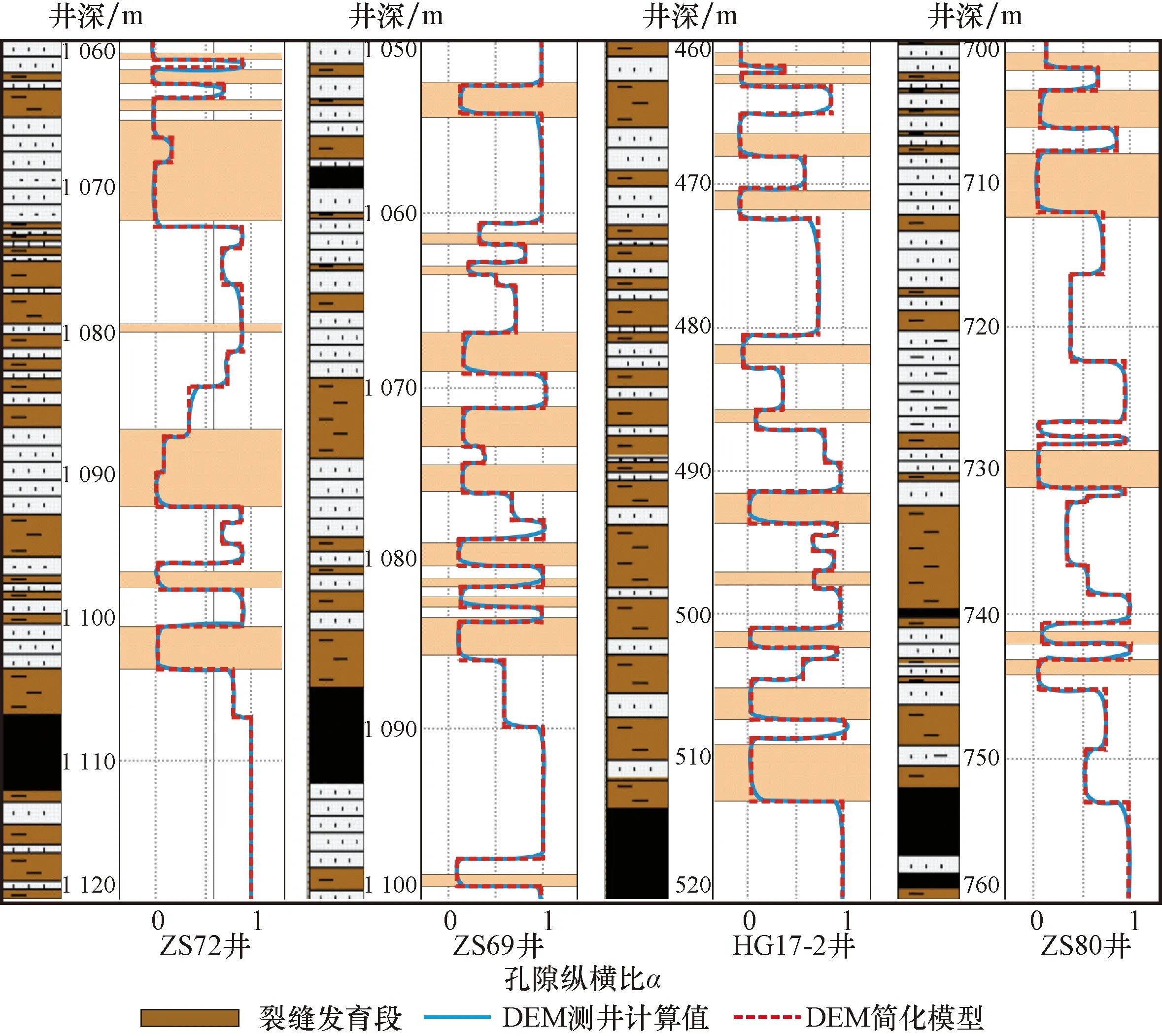
图4 部分井山西组岩石孔隙纵横比测井解释成果Fig.4 Logging interpretation results of rock pore aspect ratio in Shanxi Formation of some wells

研究区山西组主要发育4个砂组，其中Ⅱ砂组的裂缝发育程度最高，勘探潜力最大。笔者以Ⅱ砂组为例，利用测井资料对该砂组的裂缝平面分布特征进行预测，结果见图5。由图5可以看出：Ⅱ砂组的α整体较低，表明裂缝较为发育；α较小的裂缝强发育区主要分布在中南部地区及北部局部地区；该地区最大的2条边界断裂(寺头断裂及后城腰断裂)所组成的寺头_后城腰走滑断裂带的中段和南段附近地区岩石的α较低，裂缝最为发育；而该走滑断裂带北段的α相对高一些，表明裂缝发育程度相对低一些；寺头-后城腰走滑断裂带中段和南段的断距普遍大于200.00 m，断裂活动性强；而其北段的断距通常小于150.00 m，断距相对较小。这是造成该断裂带中_南段与北段裂缝发育程度出现较大差异的重要原因。

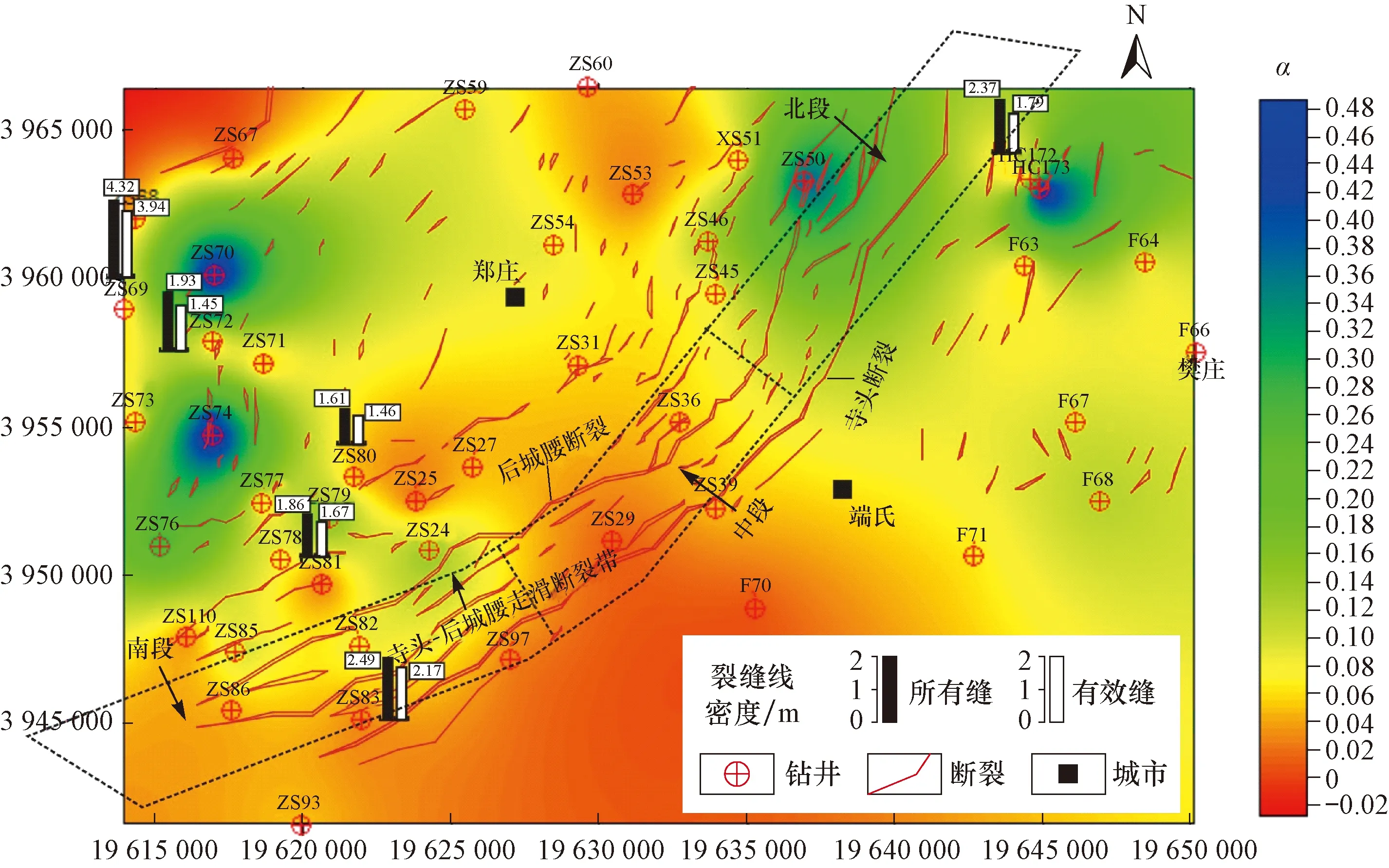
图5 研究区山西组Ⅱ砂组岩石孔隙纵横比平面分布Fig.5 Plane distribution of aspect ratio of rock pore in the sand group II of Shanxi Formation in the study area注：纵横坐标轴为大地坐标，单位为m。

测井预测结果与岩心裂缝观察结果进行对比可以看出，两者也是吻合的。ZS69井、ZS83井及HG17_2井附近的α较低，其岩心裂缝发育程度较高，有效裂缝线密度均大于1.79条/m；而ZS72井、ZS78井及ZS80井处于相对平缓的构造带及裂缝发育的边缘带，这些区域的α要相对大一些，对应裂缝密度相对小一些，其有效裂缝线密度主要为1.45～1.67条/m。整体而言，岩心裂缝观察结果与预测结果相符。

研究区东北部及西北部地区存在2个α较高的中心，代表裂缝发育程度较差，这些区域的断裂相对欠发育，构造活动较弱。整体来看，该裂缝测井预测结果与该地区目前的基本地质认识是吻合的。因此，该方法对于指导强改造区海陆过渡相煤系致密砂岩储层“裂缝甜点”预测具有一定参考价值。

3 结论与建议

1) 提出了基于动态弹性力学模型的煤系致密储层裂缝预测方法，利用寻优算法提取了煤系地层各类岩石的干岩石模量参数。单井裂缝预测结果表明，该方法的预测精度较高，预测结果与岩心裂缝实际发育程度的符合率约为90%。

2) 利用寻优算法提取了煤系地层各类岩石的模量参数，但各模量参数与各矿物组分之间的关系及相应的定量测井模型尚未建立，因此还需继续深入研究。

3) 岩石的破裂受控于岩石力学性质，且涵盖不同尺度，建议下一步进行各模量参数与不同尺度及不同类型破裂之间的关系研究。