水平振动管内液氢流动沸腾压降的数值模拟
2018-10-13商燕常华伟郑尧陈建业舒水明
商燕,常华伟, 2,郑尧,陈建业,舒水明
水平振动管内液氢流动沸腾压降的数值模拟
商燕1,常华伟1, 2,郑尧1,陈建业1,舒水明1
(1. 华中科技大学 能源与动力工程学院,湖北 武汉,430074;2. 航天低温推进剂技术国家重点实验室,北京,100028)
在液氢加注系统中,管道振动会显著影响液氢加注效率,甚至会威胁到加注过程的安全性。为了避免这种现象,确保加注过程的安全的进行,建立加注管路的三维模型,采用数值仿真的方法,从不同入口速度、振幅、频率等方面,利用CFD软件模拟并分析振动对液氢管内流动沸腾压降的影响。利用快速傅里叶变换(FFT)分析方法,得到液氢管内流动沸腾压降波动与管道振动之间的关系。研究结果表明:对液氢在输运管内流动压降影响最大的是频率,而对压降波动影响最大的是入口速度。
液氢;振动;压降;数值模拟;快速傅里叶变换
液氢作为一种清洁且高能量密度的燃料,被广泛应用于卫星、航天飞机和宇宙飞船等的运载火箭发射中,在航空推进领域中起着关键性作用。在火箭加注系统中,低温流体的管道输送过程对火箭加注系统是否成功加注起着决定性作用,因此,对低温流体在输送管道内流动换热的研究具有重大意义,而确定管路系统的振动对输送管内流体流动压降的影响是安全输送低温流体的重要部分。KIM等[1]在原有理论的基础上,通过考虑过冷度的影响,提出了一种分析流体诱发振动的方法,实验结果证实了该方法的有效性。而WIGGERT等[2−3]对考虑管道轴向振动与流体压力脉动的流固耦合4方程模型进行了研究。在输流管道振动方面,花纯利等[4−5]利用有限元方法对输液管道的振动进行了分析,得到了流体速度、压力在管道中的分布规律以及管道固有频率的影响因素;梁建术等[6]分析了高频振荡流体载荷作用下折弯式管道系统的耦合振动特性,其结果表明节流孔板对管道系统的振动有一定的抑制作用。对于液氢等深低温流体而言,还没有较准确的管道振动微分方程。对于低温气液两相流动问题,国内外学者进行了大量的研究。MIWA等[7]对管内两相流动流激振动进行了分析,且总结了近几年有关流激振动方面的研究进展,提出了减少输送管内流激振动现象的措施;CHEN等[8]基于CFD数值模拟,利用欧拉双流体模型通过分析水平圆管内固−液两相流动压降,总结出速度、固相体积分数与压降的关系;CHIAPERO等[9]研究了R134a在水平管内沸腾流动压降特性曲线,其研究结果表明压降、入口速度和入口温度与R134a在水平管内沸腾流动曲线有一定的关系;CHEN等[10]对水平微型圆管内液氮沸腾流动的摩擦压降进行了相关研究,根据实验结果拟合得到液氮在水平微型管道内沸腾流动的摩擦压降与质量流量、入口压力和热流量的关系曲线;PENDYALA等[11]对低频振荡的垂直管流压降进行了研究,结果显示速度以及雷诺数是压降的2个重要影响因素;栾骁等[12]利用AMESim软件进行仿真分析,初步得到防止液氢在输送管道内流动出现气液两相的方法;陈虹等[13]对输运管内低温流体的传热过程进行了分析,得到管路结构对热力学参数变化的影响;CHANG等[14]对液氢在弯管内流动空化现象进行了数值模拟,总结出影响空化过程的因素有入口速度、出口压力、湍流黏度以及弯管角度等;齐守良等[15]利用均相模型、L−M模型、Chisholm B系数模型和Friedel模型对微通道内液氮沸腾流动压降进行了分析和比较。目前,人们对于液氢在输流管内流动沸腾时状态参数变化的研究较少,大多是从流体诱发振动的角度出发进行研究。为此,本文作者采用CFD数值模拟的方法对液氢在水平管内流动沸腾进行研究,通过检测入口与出口处的流体压力,考虑不同入口速度、振动频率以及振幅来分析管路振动对液氢流动压降的影响,并对所检测到的压降进行快速傅里叶变换,分析液氢管内流动压降的频率,确定压降频率变化的范围,以便为低温输流管路的设计提供参考。
1 物理模型与数学模型
1.1 物理模型
液氢以一定速度从管道左侧流入,管壁保持恒壁温,加热管内流体。在流动过程中,由于液氢温度低于壁面温度,使近壁处的流体因吸热气化产生气液两相,并且随着流动的进行,气相体积分数逐渐增加,直至流出管道。在管道振动的情况下,管内流体在流动过程中还会随管道上下波动,靠近壁面处的换热增强,使湍流动能增强,此时的总压降由摩擦压降、重力压降和加速压降组成。
图1所示为液氢在水平管道内流动的物理模 型。管道在垂直速度方向振动,由于壁面热流加热而沸腾。水平管管长=2 m,内径=0.2 m。管道的结构性网格是利用Gambit2.4.6创建的,网格数为 138 240个。
1.2 数学模型
管内流动采用三维非稳态模型,在数值计算过程中采用欧拉沸腾模型中的RPI模型来模拟液氢管内沸腾流动,能量方程和动量方程采用二阶离散化,具体形式如下。

(a) 系统的物理模型;(b) 数值计算网格
1.2.1 连续性方程

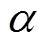
1.2.2 动量守恒方程

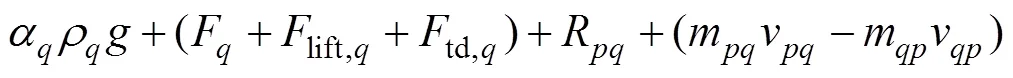
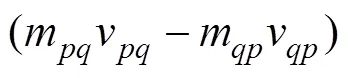
1.2.3 能量守恒方程
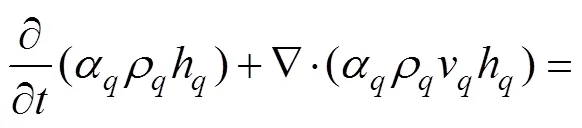
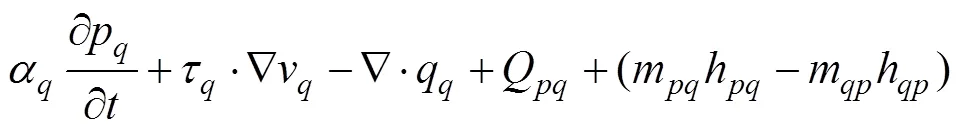

1.2.4 RPI模型
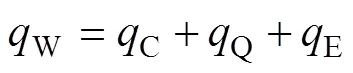

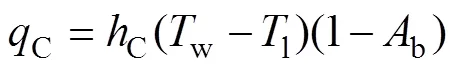
式中:C为单相换热系数,W/(m2∙K);w和l分别为壁面和液相的温度,K。
淬火热流量的计算式为
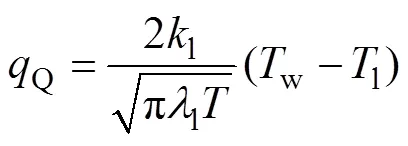
式中:l为导热系数,W/(m∙K);为周期,s;l为热扩散率,m2∙s。
蒸发热流量计算式为

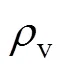
1.3 初始条件及边界条件
在初始时刻,水平管入口处液氢以恒定速度流入管内,计算域入口为速度边界条件,出口为压力出口边界条件,壁面上液相采用无滑移边界条件,壁面温度恒定为23.28 K,具体计算参数见表1。管道振动边界条件为纵向振动,采用UDF定义,即
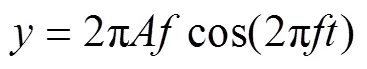
式中:为管道的时刻瞬时振动位移,m;为管道振动幅度,m;为振动频率,Hz。
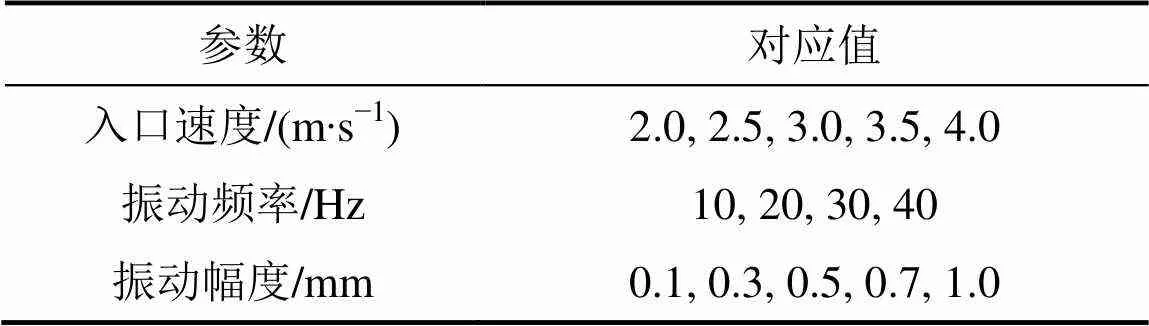
表1 数值模拟的参数范围
1.4 模型验证
由于液氢在水平振动圆管内流动沸腾压降的实验数据较少,而欧拉沸腾模型在本文模拟中是极为重要的一部分,故有必要对此计算模型进行验证。采用相同条件下的计算模型,与液氮两相沸腾流动压降的数值研究[16]中的实验结果进行类比。边界条件如下:入口过冷度为2.2 K,系统压力为0.72 MPa,质量流量为185 kg/(m2∙s)。计算8组不同热流量下的压降,热流量为1.5~2.3 kW/m2。图2所示为8组数值模拟的结果与实验结果的对比。由图2可知:压降模拟结果与实验结果的相对误差在±50%以内。因此,用来进行液氢在水平振动管道内流动沸腾压降特性的CFD数值模型是有效的。

图2 压降数值模拟值与实验结果对比
2 数值仿真及结果分析
2.1 振动对管路压降的影响
图3所示为当流速为2 m/s时,管道振动与无振动时压降的对比结果。由图3可见:管道振动时液氢沸腾流动的压降波动明显比无振动时的强;当入口速度较小(如速度为2 m/s)时,管道不施加振动的压降波动曲线近似为1条直线,而管道振动时的压降波动曲线呈现周期性的上、下波动。在输送低温流体的过程中,这种现象存在安全隐患,因此,研究管道振动对液氢流动沸腾压降的影响对设计液氢输送管道尤为重要。
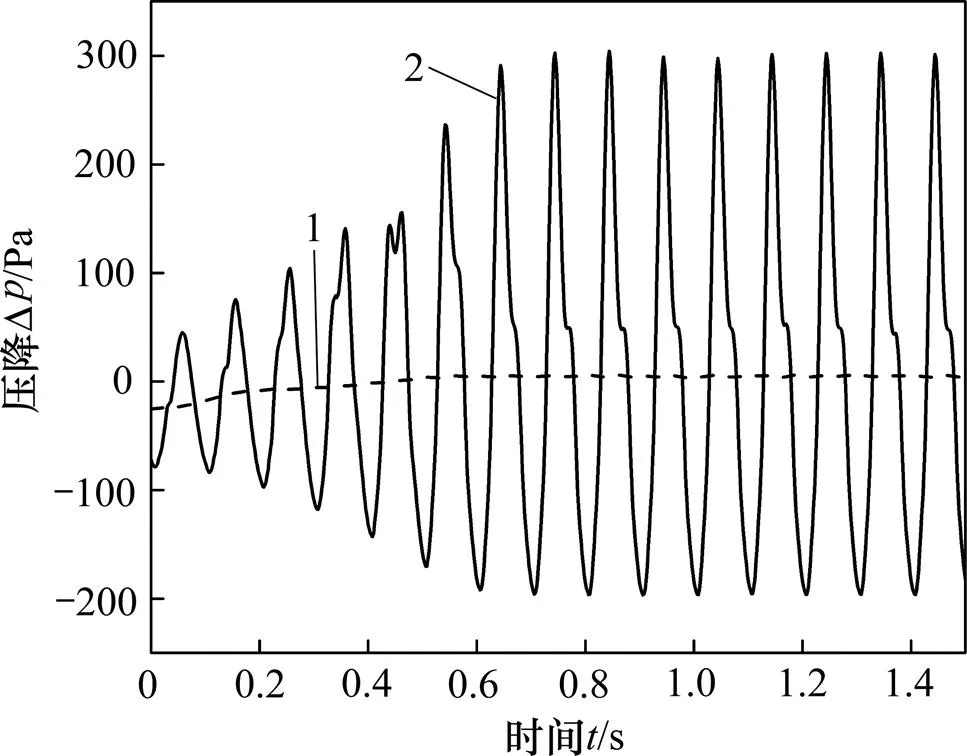
1—无振动;2—有振动。
2.2 流速对管路压降的影响
图4所示为不同流速下振动对压降的影响。由图4可见:由于对管道施加的振动频率为正弦曲线,故压降呈周期性变化;当流速为2 m/s时,压降最大波动范围为−100~400 Pa;而当流速增加到4 m/s时,其最大波动范围为−600~1 200 Pa。其原因是液氢流速越大,压降波动的频率越接近管道振动频率从而产生的压降变化越大。由此可知:在其他条件一定时,入口流速越大,压降波动越剧烈,压降变化范围也越大。
此外,在图4(c)所示的压降图中,每个周期内有2个较高峰,并且这2个较高峰均在管道振幅趋近于0 mm时发生,而在管道振动最大时,压降最小。这是因为在近壁处的表面上气泡的数量随热流量的增加而增加,而增加的气泡会在近壁处产生更大的扰动。根据模拟结果发现,在图5所示的不同压降波动下的总表面热流量变化中,压降的2个较高峰处的热流量较大,而在压降最小的时候热流量较小,因此,压降在管道振动最大时处于最小值,在管道振幅趋近于 0 mm时达到最大值。

(a) 速度为2 m/s时的压降变化;(b) 速度为4 m/s时的压降变化;(c) 振动和压降对比

(a) 压降最大时;(b) 压降最小时
2.3 振动频率及振幅对管路压降的影响
图6所示为不同管道振动频率下压降的变化。由图6可知:当管道振动频率为10 Hz时,压降最大波动范围为−600~1 200 Pa,而当频率增大到40 Hz时,压降最大波动范围为−300~1 300 Pa,其变化不明显,即频率对压降最大波动范围影响比入口流速的小。与图4相同,此时的压降图在1个周期内也存在2个波峰,其最高峰对应管道振幅趋近于0 mm时。
图7所示为管道振幅对压降的影响。由图7可知:当振幅为0.1 mm时,压降最大波动范围为−200~ 800 Pa,而当振幅增加到1 mm时,其最大波动范围为−600~1 200 Pa,即在其他条件一定时,管道振幅越大,压降波动越剧烈,并且在不同振幅下,压降变化范围明显不同。另外,与图4类似,此时的压降波动图中也在1个周期内出现了2个波峰,并且对应在振幅趋近于0 mm时。出现这种情况的原因与速度对压降波动影响的原因相同。
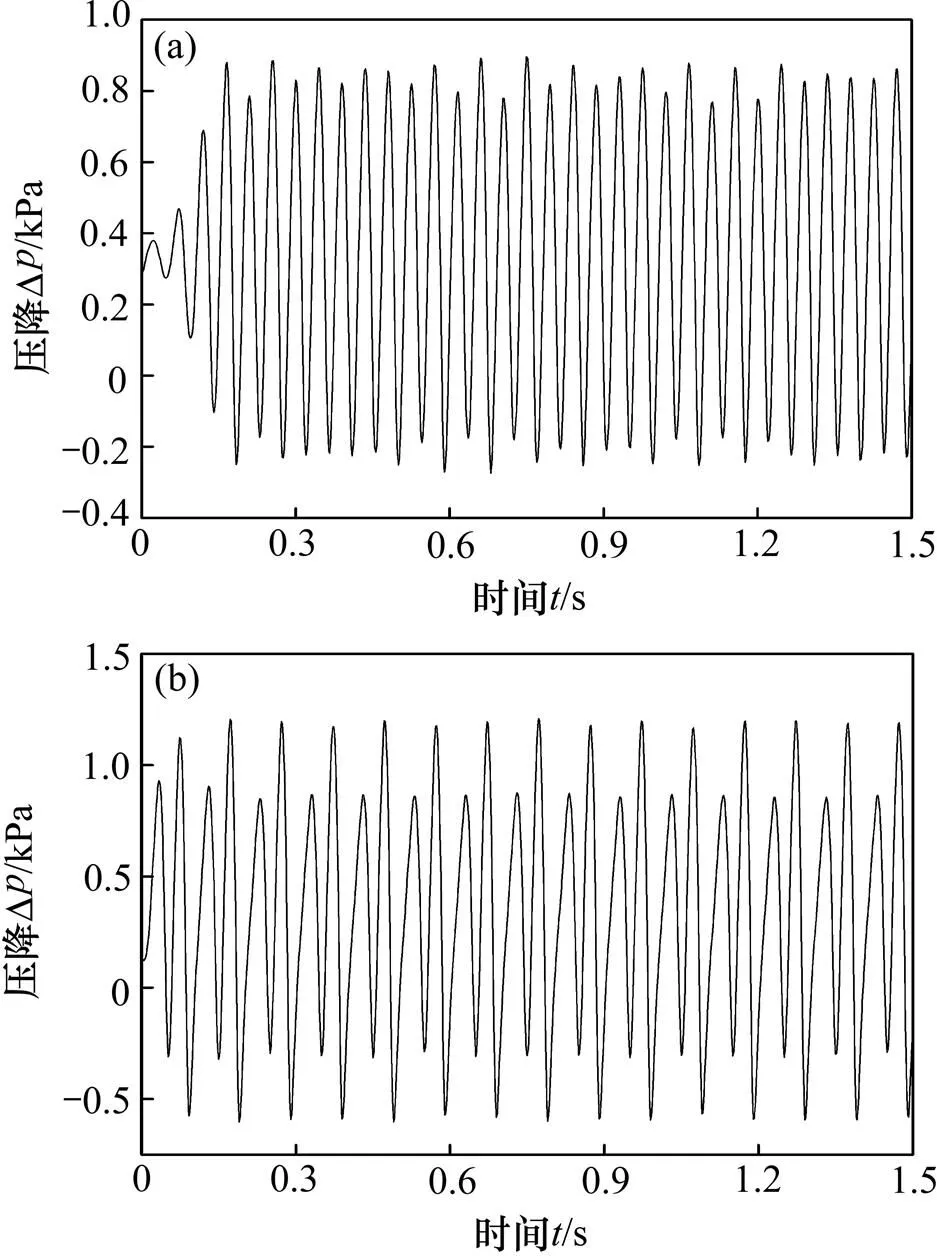
A/mm:(a) 0.1;(b) 1.0
对图4、图6以及图7中的压降求平均值∆ave,可以发现:当液体速度从2 m/s增加到4 m/s时,∆ave从112.04 Pa变化到344.49 Pa;当管道振动频率从 10 Hz增加到40 Hz时,∆ave从344.49 Pa变化到386.13 Pa;当管道振幅从0.1 mm增加到1 mm时,∆ave从338.14 Pa变化到344.49 Pa。即当速度增加1倍时,压降增加约2.5倍,然而,当振幅增加9倍时,压降变化较小。因此,在其他条件一定时,对压降变化影响最大的是速率,影响最小的是振幅。
2.4 压降变化频谱分析
为了进一步分析振动管道对液氢沸腾流动压降的影响,对压降变化进行FFT变换,如图8所示。从图8可以看出:在其他条件一定时,速度对压降波动影响较小,管道振动频率对压降影响较大,且最大频率在20 Hz附近。
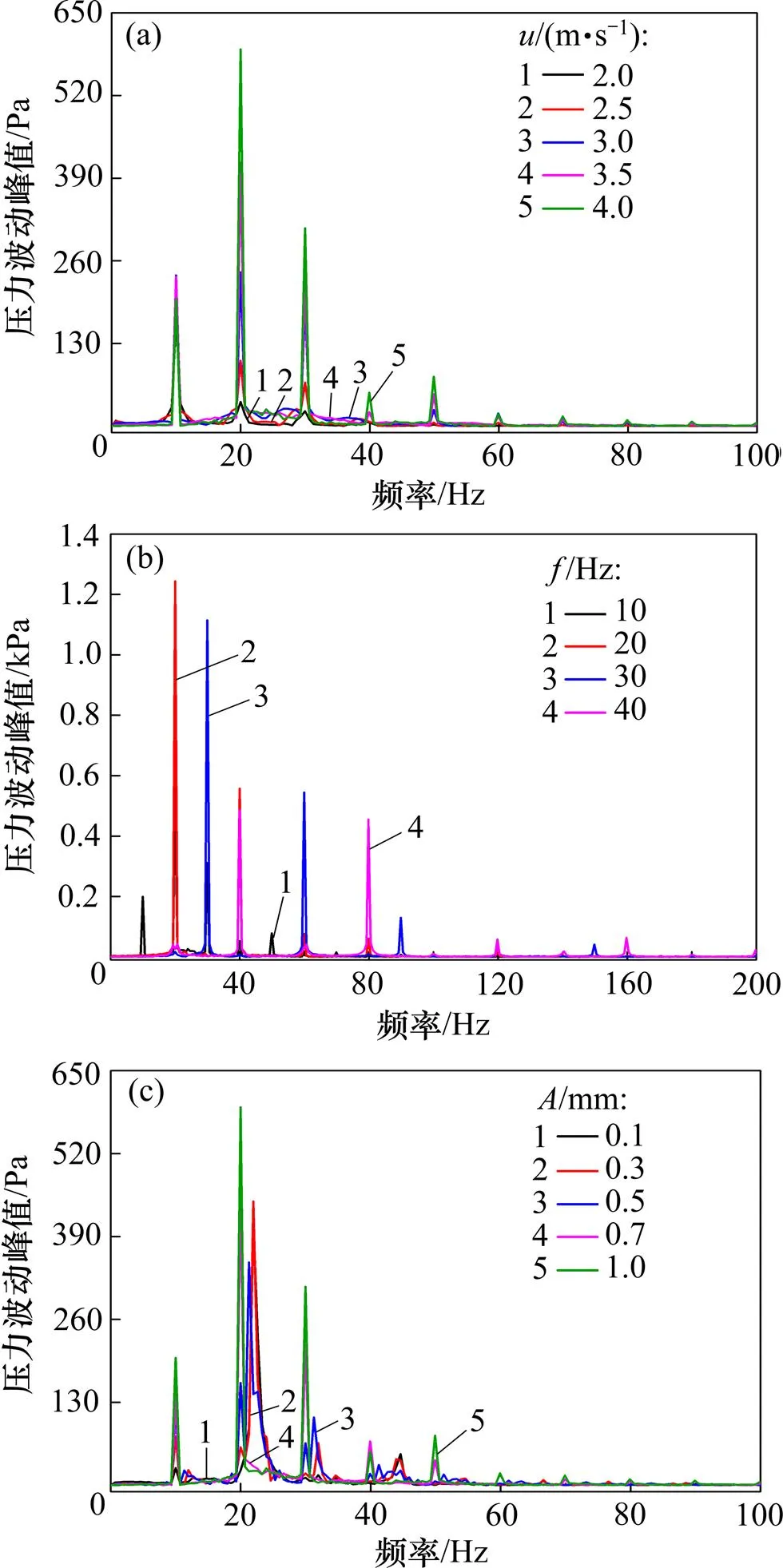
(a) 不同进口流速(f=10 Hz,A=1 mm);(b) 不同振动频率(u=4 m/s,A=1 mm);(c) 不同振幅(u=4 m/s,f=10 Hz)
在图8(a)中,不同流速下压降波动曲线均出现3个较高的峰值,而且其变化趋势均相同。在压降频率等于管道振动频率时出现第1个波峰。由图4(c)可见:第2个较高峰出现是因为在1个周期内压降波动出现2个最高点,频率叠加;而出现第3个波峰的可能原因是压降频率成倍叠加。在频谱分析图8(b)中,不同频率下的压降曲线都存在2个较高的峰值。在压降波动频率等于管道振动频率时出现第1个波峰;第2个则是因为在压降图中对应1个周期的管道振动,压降波动出现2个最高峰,频率叠加。在频谱分析图8(c)中,不同振幅下的压降曲线都有3个较高的峰值。第1个均在压降波动频率等于管道振动频率时出现的;第2个则为流体流动引起的管道振动峰;而第3个可能是在压降频率成倍叠加时出现的。
从以上速度、频率和振幅对压降影响的频谱分析图可以发现:除频率外,压降波动幅值均是在叠加频率发生时达到最大值。
3 结论
1) 液氢在水平圆管内流动沸腾时的压降与管道振动关系密切,由压降的研究结果可以发现压降波动的最高点对应管道振动振幅趋近于0 mm时,而管道振动最大时对应的是压降的最低点。
2) 速度对压降波动范围影响很大。2~4 m/s之间,随着液氢入口速度的增加,压降波动范围也随之变大。但是,对于不同振动频率下液氢流动,压降波动范围变化不大。
3) 管道振动频率对压降波动的幅值影响最大,而速度和振幅对压降波动的幅值影响相差不大。
[1] KIM B S, KIM Y K, CHOI J. Analysis of fluid induced vibration of cryogenic pipes in consideration of the cooling effect[J]. Journal of Mechanical Science and Technology, 2008, 22(12): 2375−2385.
[2] WIGGERT D C, TIJSSELING A S. Fluid transients and fluid-structure interaction in flexible liquid-filled piping[J]. Applied Mechanics Reviews, 2001, 54(5): 455−481.
[3] TIJSSELING A S. Water hammer with fluid–structure interaction in thick-walled pipes[J]. Computers & Structures, 2007, 85(11): 844−851.
[4] 花纯利, 高康, 周俊, 等. 特种输液(汽)管道振动固有特性分析[J]. 噪声与振动控制, 2013, 33(3): 60−64. HUA Chunli, GAO Kang, ZHOU Jun, et al. Analysis of characteristics of intrinsic vibration of a special liquid (gas) transfer pipeline[J]. Journal of Noise and Vibration Control, 2013, 33(3): 60−64.
[5] 武永红, 李永堂, 刘志奇. 输液管道的振动分析[J]. 振动、测试与诊断, 2013, 33(S2): 100−104. WU Yonghong, LI Yongtang, LIU Zhiqi. The vibration analysis in full liquid pipe[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(S2): 100−104.
[6] 梁建术, 王涛, 李欣业. 基于Ansys的输液管道系统的振动控制分析[J]. 机械强度, 2012, 34(4): 486−490. LIANG Jianshu, WANG Tao, LI Xinye. Vibration control analysis of liquid-conveying pipe system based on Ansys[J]. Journal of Mechanical Strength, 2012, 34(4): 486−490.
[7] MIWA S, MORI M, HIBIKI T. Two-phase flow induced vibration in piping systems[J]. Progress in Nuclear Energy, 2015, 78: 270−284.
[8] CHEN Xiaoning, WU Jiande, WANG Xiaodong. Numerical simulation of solid-liquid two phase flow in horizontal circular pipe based on CFD[C]// Control and Decision Conference (CCDC). Yinchuan, China: IEEE, 2016: 600−605.
[9] CHIAPERO E M, DODER D, FERNANDINO M, et al. Experimental parametric study of the pressure drop characteristic curve in a horizontal boiling channel[J]. Experimental Thermal and Fluid Science, 2014, 52(2): 318−327.
[10] CHEN Xingya, CHEN Shuangtao, CHEN Jun, et al.Two-phase flow boiling frictional pressure drop of liquid nitrogen in horizontal circular mini-tubes: experimental investigation and comparison with correlations[J]. Cryogenics, 2017, 83: 85−94.
[11] PENDYALA R, JAYANTI S, BALAKRISHNAN A R. Flow and pressure drop fluctuations in a vertical tube subject to low frequency oscillations[J]. Nuclear Engineering & Design, 2008, 238(1): 178−187.
[12] 栾骁, 马昕晖, 陈景鹏, 等. 液氢加注系统低温管道中的两相流仿真与分析[J]. 低温与超导, 2011, 39(10): 20−23. LUAN Xiao, MA Xinhui, CHEN Jingpeng, et al. Analysis and simulation on two-phase flow in the pipeline of liquid hydrogen filling system[J]. Cryogenics & Superconductivity, 2011, 39(10): 20−23.
[13] 陈虹, 刘超, 舒畅, 等. 输送管内低温流体滞止状态热力参数数值仿真[J]. 中南大学学报(自然科学版), 2016, 47(7): 2507−2512. CHEN Hong, LIU Chao, SHU Chang, et al. Numerical simulation of thermodynamic parameters of cryogenic fluid in stagnation state within conveying pipeline[J]. Journal of Central South University(Science and Technology), 2016, 47(7): 2507−2512.
[14] CHANG Huawei, XIE Xiaoshu, ZHENG Yao, et al. Numerical study on the cavitating flow in liquid hydrogen through elbow pipes with a simplified cavitation model[J]. International Journal of Hydrogen Energy, 2017, 42(29): 18325−18332.
[15] 齐守良, 张鹏, 王如竹, 等. 微通道中液氮的流动沸腾: 两相流动压降分析[J]. 机械工程学报, 2007, 43(5): 36−43. QI Shouliang, ZHANG Peng, WANG Ruzhu, et al. Flow boiling of liquid nitrogen in micro-tubes: two phase flow pressure drop[J]. Journal of Mechanical Engineering, 2007, 43(5): 36−43.
[16] LI Xiangdong, WANG Rongshun, HUANG Rongguo, et al. Numerical and experimental investigation of pressure drop characteristics during upward boiling two-phase flow of nitrogen[J]. International Journal of Heat and Mass Transfer, 2007, 50(9): 1971−1981.
(编辑 刘锦伟)
Numerical simulation of pressure drop with liquid hydrogen flow boiling in horizontal vibration pipeline
SHANG Yan1, CHANG Huawei1, 2, ZHENG Yao1, CHEN Jianye1, SHU Shuiming1
(1. School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; 2. State Key Laboratory of Technologies in Space Cryogenic Propellants, Beijing 100028, China)
In the liquid hydrogen filling system, pipeline vibration will significantly affect the filling efficiency of liquid hydrogen and even threaten the safety of the filling process. To avoid this phenomenon and ensure the safety of the filling process, a three-dimensional model of the filling pipeline with liquid hydrogen was established to analyze the influence of vibration on the flow boiling pressure drop under different inlet speeds, amplitudes and frequencies with numerical simulation by CFD software. The relationship between the flow boiling pressure fluctuation and the vibration of the pipeline was obtained by Fast Fourier Transform (FFT) analysis. The results show that the main factor affecting the magnitude of pressure drop of liquid hydrogen boiling flow in the pipeline is frequency, and the main factor affecting the pressure drop fluctuation is the inlet velocity.
liquid hydrogen; vibration; pressure drop; numerical simulation; FFT
10.11817/j.issn.1672-7207.2018.09.029
TK91
A
1672−7207(2018)09−2337−07
2017−10−21;
2017−11−17
航天低温推进剂技术国家重点实验室基金课题(SKLTSCP1510) (Project(SKLTSCP1510) supported by the Fund of the State Key Laboratory of Technologies in Space Cryogenic Propellants)
常华伟,博士,助理研究员,从事制冷及低温技术研究;E-mail: changhuawei@hust.edu.cn
