基于运动单元故障建模的装配可靠性控制技术
2018-10-13鞠萍华黄广全冉琰肖莉明李壮
鞠萍华,黄广全,冉琰,肖莉明,李壮
基于运动单元故障建模的装配可靠性控制技术
鞠萍华,黄广全,冉琰,肖莉明,李壮
(重庆大学 机械工程学院,重庆,400044)
为提高机电产品装配环节的可靠性,首先采用“功能—运动—动作”的结构化分解方法得到元动作单元,然后对产品历史故障数据进行分析以确定各运动单元的故障模式,并建立运动单元故障树;为提高分析效率,使用二元决策图(BDD)对故障树进行转化,得到故障树的最小割集,并根据基本事件的发生概率计算得到基本事件的重要度;然后根据80/20定律将重要度较高的事件确定为可靠性控制点,分析可靠性控制点故障的故障源,建立基于多色集合理论的故障与故障源间的布尔关系矩阵,提出在装配过程中针对各主要故障原因的可靠性控制措施。研究结果表明:该故障建模和可靠性控制技术能够有效提高装配过程中的可靠性。
功能结构化分解;故障树分析;多色集合理论;装配可靠性
装配是将各种不同的零部件组装成一个具有一定功能整体的过程。装配环节的质量控制是保证产品质量的重要环节,装配不良是导致产品故障的重要因素。因此,确保装配过程中的产品质量控制,对于提高产品质量具有非常重要的意义[1−2]。要提高产品装配可靠性,故障分析是基础,先通过故障分析找出可靠性薄弱环节,再采取必要的保障措施以提高产品可靠性,所以,故障分析在产品装配可靠性提升过程中具有重要作用。目前故障分析方法一般有故障树分析法(fault tree analysis, FTA)和失效模式与影响分析(failure mode and effects analysis, FMEA)[3],其中故障树分析法已经在航空、电子等领域得到应用。FTA能够找出故障的相互联系,便于系统的管理和维修[4]。因此,本文作者采用故障树分析法来对产品故障进行分析。为实现元动作单元与机床可靠性的定量关系研究,提出建立模块化故障树模型的思路。模块化故障树不引入其他基本事件,也不改变故障树的结构,仅是对模块进行重组,且利用其子树能够提高建模的效率,节省时间。对于复杂的机电产品,从整体研究往往很困难,必须将其进行分解,化繁为简。为此,以产品的基本运动功能为出发点,将整机的运动功能分解为中间层的运动单元和最底层的元动作单元,建立以运动单元为基础的模块化故障树。为提升效率和计算速度,利用BDD分析FTA,求得故障树的最小割集。通过对故障树的定量计算,确定基于元动作粒度的可靠性控制点。目前,人们针对如何提高产品的装配质量开展了许多研究。SUZUKI等[5]提出了一种装配可靠性评价方法(assembly reliability evaluation method, AREM),通过分析设计因素和车间因素对装配故障率进行了定量研究;SU等[6]对设计复杂度评价方法进行了改进,建立了复印机产品人为装配缺陷的二元统计模型,对装配质量进行预测;王永等[7]针对装配规划分解问题,提出了装配单元规划方法;邓明星等[8]提出了一种基于蚁群算法的改进装配序列规划方法,根据装配优先关系,制定了一种装配序列规划方法来提高产品的装配质量;王小巧等[9]提出一种基于装配损失−控制阀模型的装配质量研究方法,通过对影响产品质量的多载荷影响因子的控制,对产品装配质量进行优化;解维德[10]提出根据不良装配记录确定装配工艺中关键薄弱环节的方法,并建立关键薄弱质量控制点,通过对控制点装配工艺的改进来提高产品的装配质量。上述研究对产品的装配过程可靠性建模和预防提供了有价值的理论和方法,但其都是以产品结构或者功能部件为研究对象,面对的是静态对象,分析方法没有与产品的运动功能联系起来,且没有落实到零件上。本文作者从动态角度将产品按照运动功能进行分解,根据故障模式和分解结构建立关键故障运动单元模块化故障树;在分析得到可靠性控制点以后,通过对可靠性控制点的故障源进行分析,利用多色集合理论建立所有故障源和主要故障之间的布尔关系矩阵;最后通过对故障源和主要故障之间相对关系的分析,确定各主要故障的故障源。针对故障源制定装配过程可靠性提升措施,为提高产品的可靠性提供参考依据。
1 运动单元故障的提取方法
提高整机的可靠性,要有可行的可靠性控制措施,常用的办法是分析产品现有的故障,得到质量控制点并制定有针对性的措施。因此,产品的故障数据分析以及质量控制点的提取显得相当重要。基于上述分析,提出产品可靠性提升流程,如图1所示。
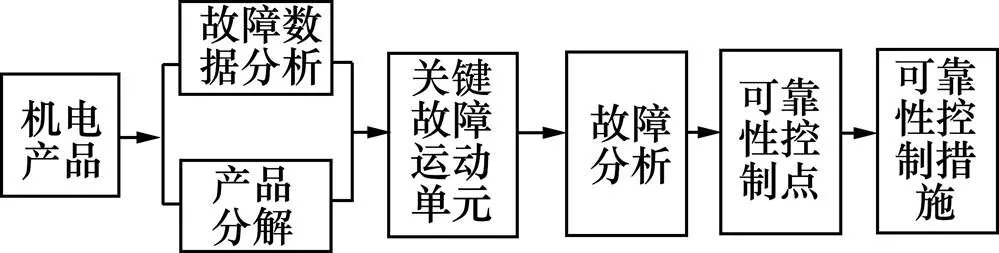
图1 产品可靠性提升流程
1.1 运动单元的建立
分析产品的历史故障数据时,应结合产品的结构化分解结果。复杂机电产品结构化分解过程的建模可以从运动角度出发,考虑机床通过最小的动作来实现其功能的过程,即通过“功能—运动—动作”的分解方法对其进行结构化分解,如图2所示。

图2 基于动作分解的结构化分解模型
由图2可知:机电产品要实现整机的运动功能,需要相应的部件子功能去实现,部件子功能的实现依靠相应的运动,运动的实现又依靠相应的动作,即“功能(function)—运动(motion)—动作(action),FMA”。在此把结构关系相对独立、能够实现一定动作目标或达到一定目的。可控可分析不需要(也不能)再细分的动作单元称为元动作(meta-action)[11]。如某加工中心整机要实现零件的各种加工工序,B轴工作台就要能够正常升降、回转。要实现B轴工作台的回转运功,伺服电机、蜗轮、蜗杆、回转油缸都要能够正常动作,产品的最后一层动作即为元动作(如蜗杆、蜗轮的转动)。由伺服电机、蜗轮、蜗杆、回转油缸等元动作单元动作所产生的B轴回转即为运动。
1.2 运动单元关键故障的提取
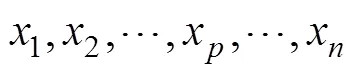
2 运动单元的故障分析
确定关键故障以后,使用FTA构建关键故障故障树,然后使用BDD对FTA的计算过程进行优化。
2.1 运动单元的故障树分析
为建立运动单元与装配可靠性的定量关系,使用FTA分析关键故障,并提出建立运动单元模块化故障树的思路。模块化故障树不引入其他基本事件,也不改变故障树的结构,仅是对模块进行重组,且利用其子树能够提高建模的效率,节省时间。文献[12]提出通过建立元动作单元故障树对机床进行故障分析,但在实际中机电产品的故障通常为运动形式的故障。而由图2可知:运动单元由若干个元动作单元组成,任何一个元动作单元发生故障,运动单元就会发生故障,且元动作单元之间存在一定的耦合关系,导致运动单元故障的元动作单元的确定和提取有一定困难,对于结构复杂、功能多、动作多的产品直接分析元动作故障单元显得不全面且可能发现不了主要故障点。因此,本文作者提出以运动故障为顶事件来建立故障树,这样既不会改变元动作单元故障树的形状,也能在故障树中找出元动作之间存在的联系,提取出比较准确、完善的可靠性控制点,且在主要故障的提取上比原方法准确、高效。基于运动单元的故障树模型如图3所示。
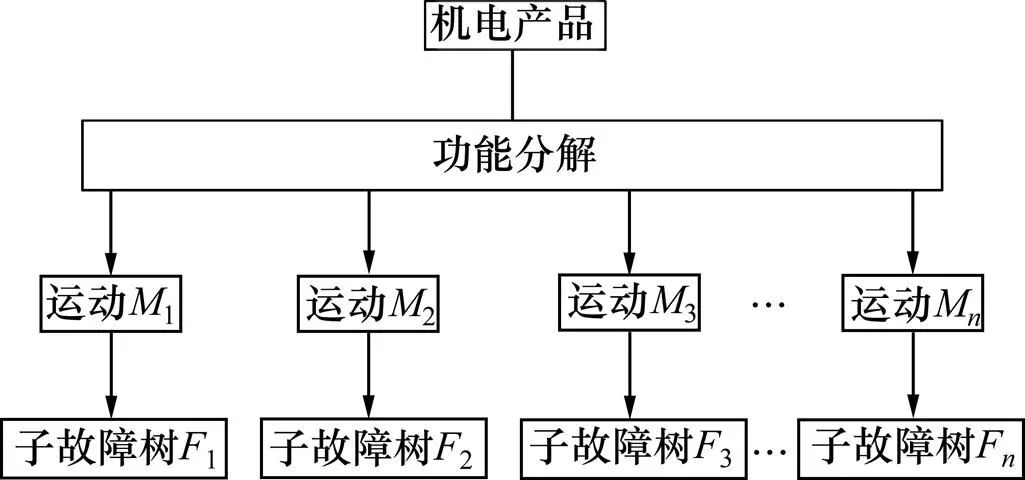
图3 基于运动单元的故障树模型
2.2 故障树计算的优化分析
FTA是目前应用非常普遍的故障分析方法,但使用FTA对复杂的系统进行计算时一般很繁杂,会产生向下展开结点的组合爆炸以及难以求解的问题[13−14]。BDD是分析FTA的一种新的方法,利用BDD分析FTA有2种优点:一是能够容易得到故障树的最小割集;二是能构造基本事件的关键函数,利用计算机求解各部件的结构重要度和概率重要度[15−16]。为求运动单元故障树的最小割集,将FTA转换为BDD,然后进行故障树的定量分析。

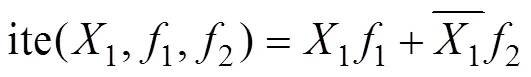
将故障树转换到BDD时,需从故障树的底层自下而上,使用ite结构对故障树进行编码转换,直到得到顶层事件的BDD。
假设和是故障树中的2个基本事件,求取顶事件的BDD。求解过程中需遵循以下合并规则,设ite,1,2),ite(,1,2)。
1) 若<(基本事件的顺序上<),则有
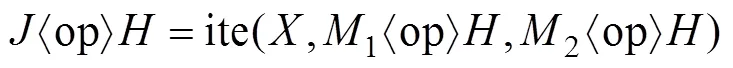
2) 若=(基本事件的顺序上=),则有:
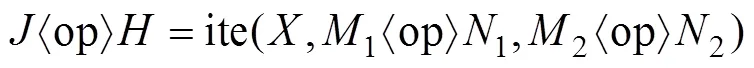
利用BDD法可以简化复杂的故障树求解最小割集的过程,但是在将FTA转化为BDD的过程中,最后产生的BDD节点数依赖于底事件的排列次序,不当的排序会导致BDD规模呈指数增长[17],而对基本事件进行合理的排序便会有效减小BDD的规模[18],因此,对底事件合理排序是FTA转化为BDD过程中的关键。本文作者先利用基本事件的排序法则对故障树的底事件进行排序,然后利用ite结构分析方法将故障树转化为BDD;利用BDD求出故障树最小割集,然后对故障进行定量分析;计算得出基本事件的概率重要度和相对概率重要度后,通过对比重要度便可以确定关键故障。

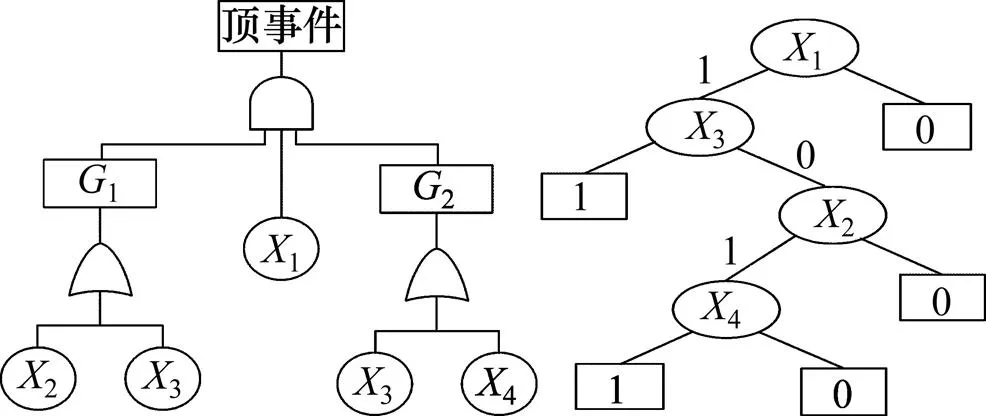
图4 故障树和转换后的BDD图
3 基于多色集合理论的故障与故障源建模
通过关键故障分析得出质量控制点后,应对质量控制点对应的故障(以下简称故障)进行溯源以找到故障发生单元并对其采取有效的可靠性控制措施。而复杂产品的装配可靠性、故障、故障源之间的关系复杂,弄清楚它们之间的对应关系也是一个难点。
多色集合理论是俄罗斯巴甫洛夫教授提出的,该理论能够清楚表达集合的统一颜色、集合元素、其元素颜色之间的关系。对组成零件较多的机电产品进行分析时,可利用它求解复杂空间中元素与整体的关 系[19−21]。而产品的装配可靠性与故障源之间的逻辑关系与多色集合中组成多色集合的元素的个人颜色的存在是统一颜色存在首要原因的逻辑关系相似,因此,可将主要故障组成1个集合,各主要故障为该集合中的元素,故障源为元素的个人颜色。这样便能找出与众多故障相对应的故障源,建立故障与故障源之间的对应关系,从而为可靠性控制指明方向。

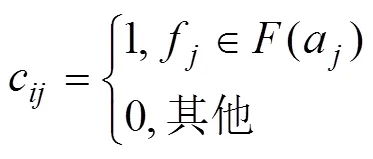
4 实例分析
通过对某型号加工中心2012—2016年这5年间的故障数据进行整理,发现该型号机床的托盘交换架故障率较高,占主要故障的16.83%,故在此选择托盘交换架进行分析。机床要实现零件的加工,托盘交换架功能组必须完成相应的运动,如托盘交换架回转、托盘交换架的升降等。而实现托盘交换架的回转运动要通过伺服电机转动带动凸轮本体上升,然后凸轮转动,凸轮与交换架本体通过螺钉、螺母链接,螺杆一转动便带动托盘交换架回转体转动进而实现托盘交换架的回转运动。而托盘交换架的升降运动则是靠托盘交换架升降油缸的进油、排油导致升降油缸内活塞的升降来带动交换架的升降来实现的。
4.1 托盘交换架运动单元故障的提取及分析
通过上述分解思路,按照图2中“功能—运动—动作”的分解模型对托盘交换架进行结构化分解,结果如图5所示。
要分析托盘交换机的故障,首先要找到其关键故障。通过对其历史故障数据进行分析发现该托盘交换架功能组故障中的回转运动失效的发生率较高,占故障的31.4%。所以,在此选择“托盘交换架回转失效”作为关键故障,并利用FTA进行故障分析。由于托盘交换架回转运动下的元动作单元较多,且单元之间存在相互影响,分析元动作单元的故障可能导致分析结果不全面,因此,选择“托盘交换架回转失效”作为故障树的顶事件来构建运动单元故障树,如图6所示。其中A,B,C,D,E和F分别为转移事件。
构造出故障树之后,对各底事件的重要度进行计算,甄选出对FTA顶事件“托盘交换架回转失效”影响比较大的底事件作为可靠性控制点。由前面的分析可知:为定量计算故障树,可先将故障树转化为BDD,利用BDD求出故障树的最小割集,然后进行计算。
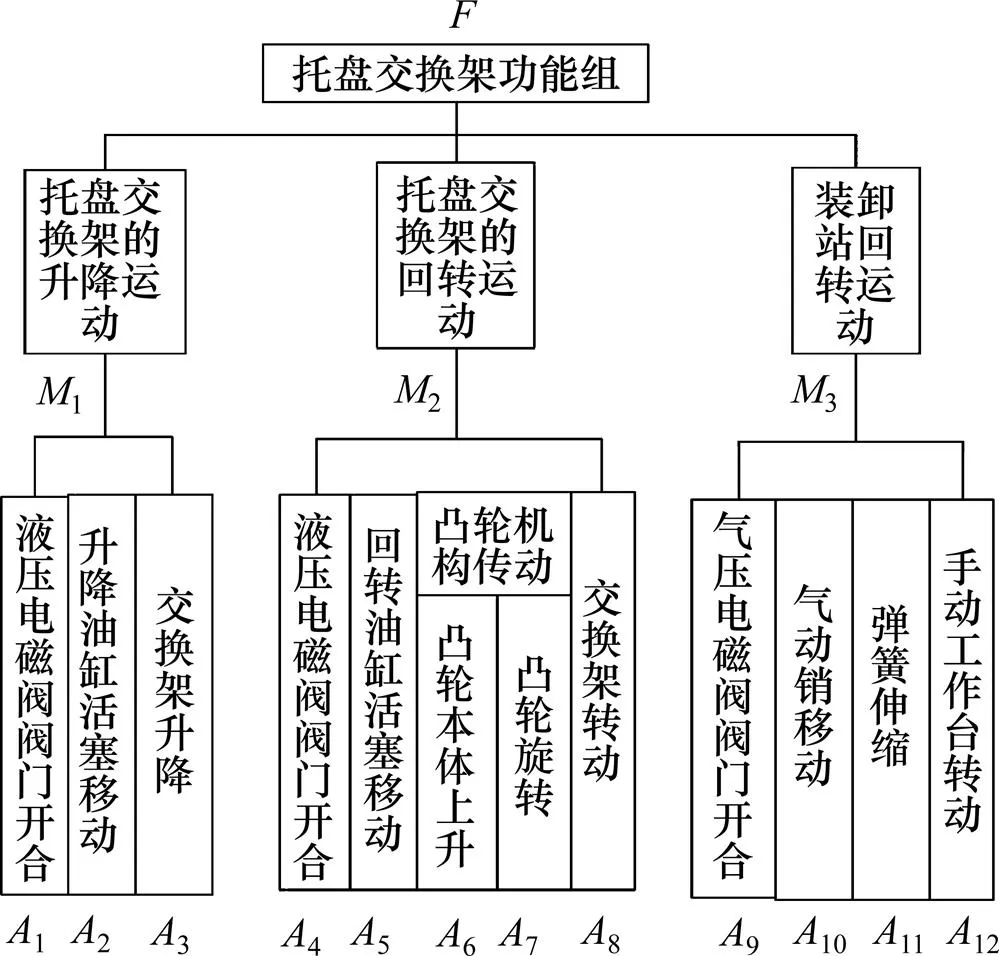
图5 托盘交换架基于动作的结构化分解
4.2 托盘交换架故障树计算的优化分析
为了求得“托盘交换架回转失效”故障树的最小割集,需要将故障树基本事件进行排序,然后转化为BDD。为了简化计算规模,在此分别对“托盘交换架回转失效”故障树中的元动作层故障树进行BDD转化。
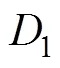
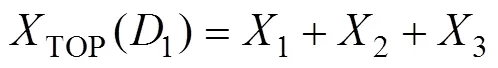
(6)
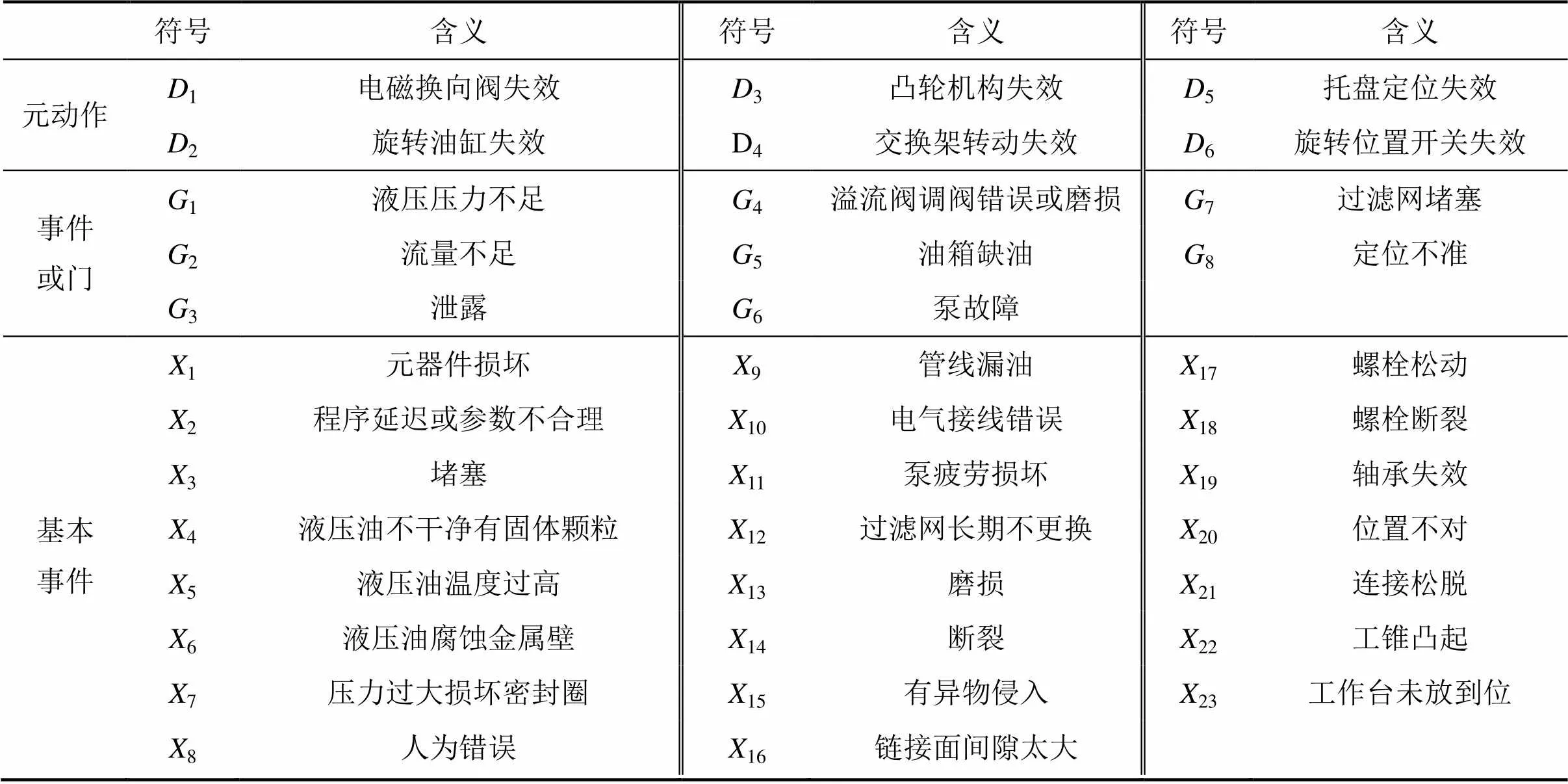
表1 托盘交换架回转运动故障树各符号含义
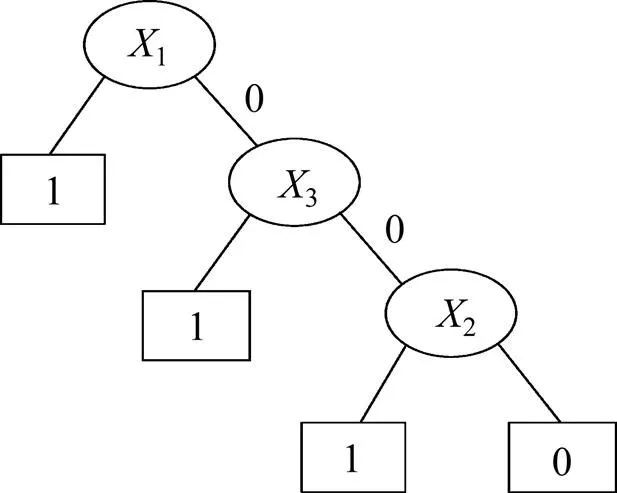
图7 元动作D1故障树转化的BDD
1元动作对应的BDD如图7所示。
元动作1子故障树对应的最小割集为{1}, {2}, {3}。
同理可得其他元动作的最小割集:元动作2子故障树的最小割集为{4}, {5}, {6}, {7}, {8}, {9}, {10}, {11}, {12};元动作3子故障树的最小割集为{13}, {14}, {15}, {16};元动作4子故障树的最小割集为{17}, {18}, {19};元动作5子故障树的最小割集为{15}, {22}, {23};元动作6子故障树的最小割集为{20}, {21}, {2}, {4}。
故障树顶事件“托盘交换架回转失效”(设顶事件为TOP)的计算公式为
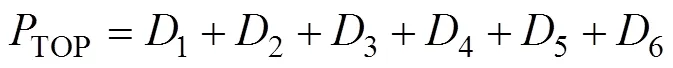
根据FTA转换为BDD需遵循的规则,可以求出故障树顶事件对应的ite结构和BDD图(过程略),则“托盘交换架回转失效”故障树对应的故障树的最小割集为{1}, {2}, {3}, {4}, {5}, {6}, {7}, {8}, {9}, {10}, {11}, {12}, {13}, {14}, {15}, {16}, {17}, {18}, {19}, {20}, {21}, {22}, {23}, {4,12}。
根据该型号机床托盘交换架基本事件的相关数据,利用BDD求得的故障树最小割集可以求出“托盘交换架回转失效”故障树各基本事件概率重要度和相对概率重要度,如表2所示。
根据计算的结果,可以确定重要度较大的事件分别为1,17,3,21,19,11,13,12,16和14。这些基本事件对托盘交换架的可靠性影响较大,因此,将其确定为可靠性控制点。
4.3 托盘交换架功能组多色集合故障与故障源建模分析
控制点确定以后分析所有故障源,找出故障与故障源的对应关系,然后,制定相应的可靠性控制措施,提高托盘交换架的装配可靠性。
根据分析可知装配环节导致托盘交换架回转失效的故障源有:1) 毛刺未除干净;2) 缸体口未倒角;3) 装螺钉时未按照力矩要求;4) 感应开关故障;5) 未按装配位置参数要求安装;6) 装配时未检查密封圈质量;7) 跳动性差;8) 蜗杆、涡轮齿磨损;9) 使用时未按要求操作;10) 未定期清理异物;11) 使用气源干燥性差;12) 未定期更换;13) 未定量化装配;14) 未调整好润滑参数;15) 参数设置不合理。
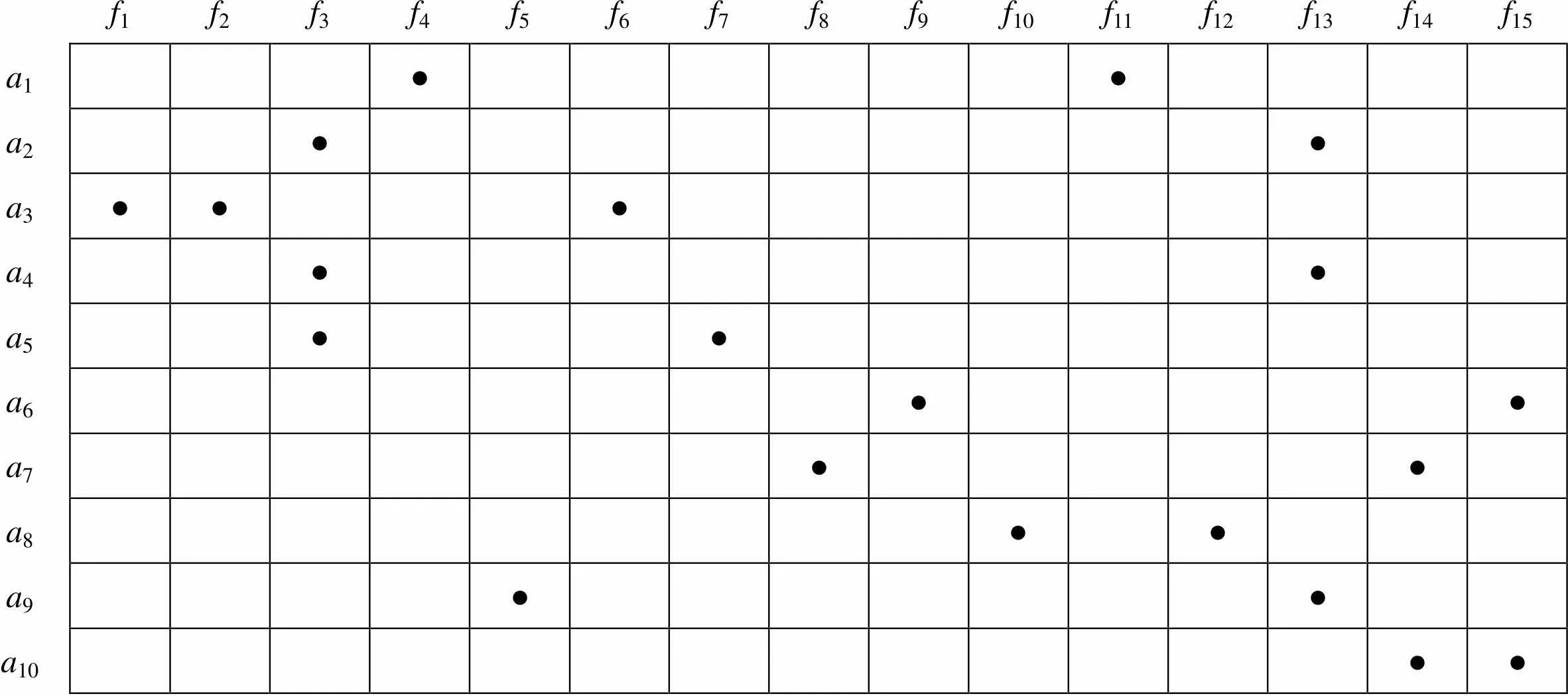
结合4.2节中确定的主要可靠性控制点及基于多色结合的故障与故障源建模方法,可得故障={1,2, …,10},故障源={1,2, …,15}。a故障受f故障源影响时,c=1,在布尔矩阵表格中用黑色原点表示;a故障点不受f故障源影响时,c=0,用空白格表示(其中=1, 2, …, 10;=1, 2, …, 15)。托盘交换架各主要故障多色集合布尔矩阵如图8所示。
由图8及多色集合理论将各故障源与托盘交换架装配过程可靠性之间的布尔关系模型表示为
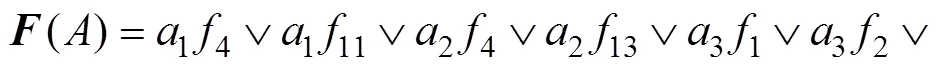
(8)
由式(8)可以直观地看出影响托盘交换架装配可靠性的故障及对应的故障源,从而可以有针对性地采取可靠性控制措施对产生故障的因素进行控制。根据可靠性知识,通过分析托盘交换架各故障的故障源,制定相应提高托盘交换架装配可靠性的控制措施。托盘交换架可靠性部分控制措施如表3所示。
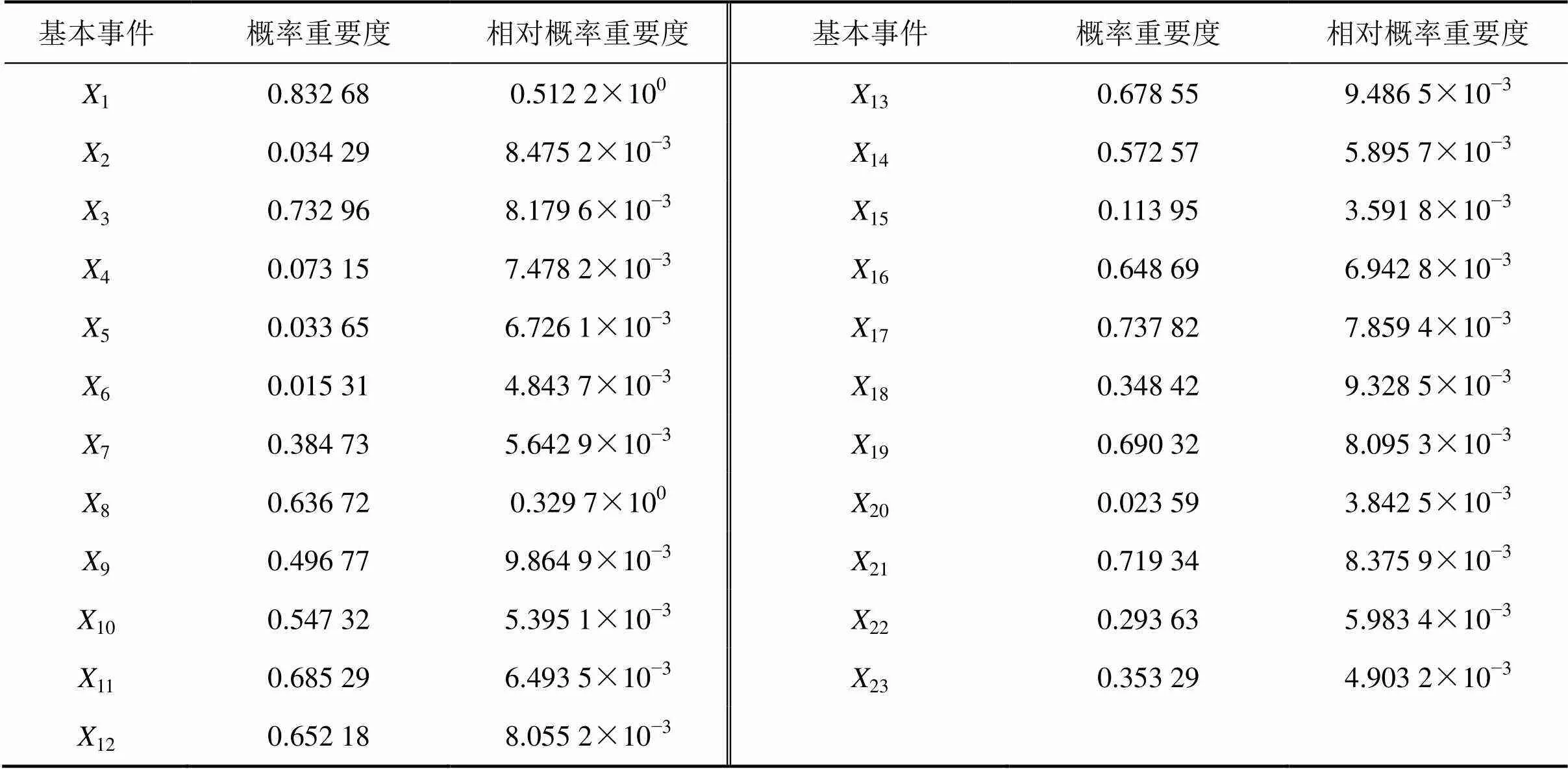
表2 托盘交换架各基本事件结构重要度和概率发生重要度
f1f2f3f4f5f6f7f8f9f10f11f12f13f14f15 a1●● a2●● a3●●● a4●● a5●● a6●● a7●● a8●● a9●● a10●●
图8 托盘交换架故障原因的多色集合
Fig. 8 Polychromatic sets of fault causes of tray exchanger

表3 托盘交换架可靠性控制措施
5 结论
1) 对机电产品进行结构化分解,通过对产品的历史故障数据进行分析确定关键故障运动单元。
2) 利用FTA和BDD对关键故障运动单元进行分析,确定可靠性控制点;通过分析装配环节导致控制点故障发生的故障源,利用多色集合理论建立故障与故障源的布尔矩阵模型,确定装配可靠性与各故障点的布尔或关系,并分析得到故障与故障源的对应关系。
3) 最后对故障源进行分析,制定装配过程的可靠性控制措施,为提高产品装配可靠性提供保障。
[1] 江荣汉. 工程系统可靠性分析基础[M]. 长沙: 湖南大学出版社, 1987: 13−18. JIANG Ronghan. Reliability analysis on engineering system[M]. Changsha: Hunan University Press, 1987: 1−3.
[2] 张根保, 葛红玉, 刘佳, 等. 可靠性驱动的装配过程建模及预测方法[J]. 计算机集成制造系, 2012, 18(2): 249−355. ZHANG Genbao, GE Hongyu, LIU Jia, et al. Assembly process modeling and prediction of reliability-driven[J]. Computer Intergrated Manufacturing Systems.2012, 18(2): 249−355.
[3] 龚庆祥. 型号可靠性工程手册[M]. 北京: 国防工业出版社, 2007: 150−163. GONG Qingxiang. Model reliability handbook[M]. Beijing: National Defense Industry Press, 2007: 150−163.
[4] 罗巍. 数控机床故障分析与可靠性评价技术的研究[D]. 吉林: 吉林大学机械科学与工程学院, 2011: 29−33. LUO Wei. Research on failure analysis and reliability evaluation technology for CNC machine tool[D]. Jilin: Jilin University. College of Mechanical Science and Engineering, 2011: 29−33.
[5] SUZUKI T, OHASHI T, ASANO M, et al. AREM shop evaluation method[J]. CIRP Annals Manufacturing Technology, 2004, 53(1): 43−46.
[6] SU Qiang, LIU Lei, WHITNEY D E. A systematic study on prediction model for operator induced assembly defect based on assembly complexity factors[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems & Humans, 2010, 40(1): 107−120.
[7] 王永, 刘继红. 面向协同装配规划的装配单元规划方法[J]. 机械工程学报, 2009, 45(10): 172−179. WANG Yong, LIU Jihong. Assembly unit partitioning for collaborative assembly planning[J]. Journal of Mechanical Engineering, 2009, 45(10): 172−179.
[8] 邓明星, 唐秋华, 雷喆. 基于蚁群算法的改进装配序列规划方法[J]. 武汉大学学报(工学版), 2013, 46(2): 246−252. DENG Mingxing, TANG Qiuhua, LEI Zhe. A novel approach for assembly sequence planning based on ant colony algorithm[J]. Engineering Journal of Wuhan University, 2013, 46(2): 246−252.
[9] 王小巧, 刘明周, 葛茂根, 等. 基于混合粒子群算法的复杂机械产品装配质量控制阀优化方法[J]. 机械工程学报, 2016, 52(1): 130−138. WANF Xiaoqiao, LIU Mingzhou, GE Maogen, et al. Online control threshold optimization for complex mechanical products assembly process based on hybrid genetic particle swarm optimization[J]. Journal of Mechanical Engineering, 2016, 52(1): 130−138.
[10] 解维德. 重型数控机床装配工艺可靠性保障方法的研究[D]. 吉林: 吉林大学机械科学与工程学院. 2016: 38−52. XIE Weide. Research on protection methods of reliability assembly process of heavy CNC machine tools[D]. Jilin: Jilin University. College of Mechanical Science and Engineering, 2016: 38−52.
[11] 李冬英. 数控机床装配质量建模与诊断技术研究[D]. 重庆: 重庆大学机械工程学院, 2014: 23−24. LI Dongying. Research on quality modeling and diagnosis technology for the assembly process of CNC machine tool[D]. Chongqing: Chongqing University. College of Mechanical Engineering, 2014: 23−24.
[12] 张根报, 张恒, 范秀君, 等. 数控机床基于FMA的功能分解与可靠性分析[J]. 机械科学与技术, 2012, 31(4): 528−533. ZHANG Genbao, ZHANG Heng, FAN Xiujun, et al. Function decomposition and reliability analysis of CNC machine using function−motion−action[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(4): 528−533.
[13] CONTINI S, MATUZAS V. Analysis of large fault trees based on functional decomposition[J]. Reliability Engineering and System Safety, 2011, 96(3): 383−390.
[14] 陈传海, 杨兆军, 陈菲, 等. 基于BDD技术的数控机床故障树分析[J]. 工程与实验, 2010, 50(3): 13−16. CHEN Chuanhai, YANG Zhaojun, CHEN Fei, et al. Fault tree analysis on CNC machine tools based on BDD technology[J]. Engineering & Test, 2010, 50(3): 13−16.
[15] 徐亨成, 张建国. 基于BDD技术下的故障树重要度分析[J]. 电子机械工程, 2003, 19(6): 1−4. XU Hengcheng, ZHANG Jianguo. The importance analysis of fault tree based on the binary decision diagrams(BDD) technique[J]. Electro−Mechanical Engineering, 2003, 19(6): 1−4.
[16] 于捷, 孙立大, 石耀霖, 等. 基于BDD技术的数控机床故障树重要度分析[J]. 机床与液压, 2008, 36(12): 186−189. YU Jie, SUN Lida, SHI Yaolin, et al. Analysis of fault tree importance od CNC machine tools based on BDD[J]. Machine Tool & Hydraulics, 2008, 36(12): 186−189.
[17] REMENYTE P, ANDEREWS J D. An enhanced component connection method for conversion of fault trees to binary decision diagrams[J]. Reliability Engineering and System Safety, 2008, 93(10): 1543−1550.
[18] FAUSTO P, JESUS M. Identification of critical components of wind turbines using FTA over the time[J]. Renewable Energy, 2015, 87(2): 869−883.
[19] 赵姗姗, 李宗斌. 基于多色集合的装配序列形式化推理方法[J]. 计算机集成制造系统, 2008, 14(8): 79−86. ZHAO Shanshan, LI Zongbin. Formalization reasoning method for assembly sequences based on polychromatic sets[J]. Computer Intergrated Manufacturing Systems, 2008, 14(8): 79−86.
[20] 蒋科, 刘检华, 宁汝新, 等. 基于多色集合理论的几何公差信息推理及其规范性验证[J]. 计算机集成制造系统, 2015, 21(3): 593−605. JIANG Ke, LIU Jianhua, NING Ruxin, et al. Geometric tolerances reasoning and its specification verification based on polychromatic sets theory[J]. Computer Integrated Manufacturing Systems, 2015, 21(3): 593−605.
[21] 杨沁, 许祥, 陈李云, 等. 基于多色集合理论的微线段齿轮表面工程技术工艺建模[J]. 中国机械工程, 2016, 27(6): 815−821. YANG Qin, XU Xiang, CHEN Liyun, et al. Micro segment gear surface engineering process modeling based on polychromatic sets[J]. China Mechanical Engineering, 2016, 27(6): 815−821.
(编辑 伍锦花)
Reliability control method of assembly process of products based on motion unit fault model
JU Pinghua, HUANG Guangquan, RAN Yan, XIAO Liming, LI Zhuang
(College of Mechanical Engineering, Chongqing University, Chongqing 400044, China)
To enhance the reliability of assembly process of electromechanical products, the method of structural decomposition of “function−motive−action” based on basic motor function was proposed. Then the fault mode of motive units were determined through analysis on failures data of products, and the fault tree of motive unit was established. To improve efficiency of analysis, the fault was translated into binary decision diagrams (BDD) for optimization. The minimal cut set of fault tree was obtained, and the importance of basic events was calculated according to the occurrence probability of basic events. According to the 80/20 rule, the events with higher importance were identified as reliability control points. Fault sources of reliability control point faults were analyzed. Polychromatic sets theory was used to establish the Boolean relationship matrix between fault and fault source, and the control measures for reliability of main factors were proposed. The results show that the proposed method is effective in improving reliability for assembly process.
functional structural decomposition; fault tree analysis; polychromatic sets theory; assembly reliability
10.11817/j.issn.1672-7207.2018.09.012
TH165+4
A
1672−7207(2018)09−2197−09
2017−09−09;
2017−10−19
国家自然科学基金资助项目(51575070);国家科技重大专项计划(2015ZX04003-003,2016ZX04004-005) (Project(51575070) supported by the National Natural Science Foundation of China; Projects(2015ZX04003-003, 2016ZX04004-005) supported by the National Science and Technology Major Program)
鞠萍华,博士,副教授,从事机械测试技术、机械设备故障诊断、机床设计与制造、机电产品可靠性等研究;E-mail: jupinghua@163.com
