东北地区机场混凝土道面温度翘曲试验研究
2018-10-13张万志徐帮树李兵杨来华连艳武
张万志,徐帮树,李兵,杨来华,连艳武
东北地区机场混凝土道面温度翘曲试验研究
张万志1,徐帮树1,李兵1,杨来华2,连艳武2
(1. 山东大学 岩土与结构工程研究中心,山东 济南,250061;2. 中铁十二局集团有限公司,山西 太原,030024)
为了研究我国东北地区机场水泥混凝土道面板板角温度分布规律及温度−应力/应变关系,依托新建松原查干湖机场道面工程开展道面温度翘曲试验,应用智能温度、应变传感器监测板角不同深度处的温度与应变、应力日间变化和季节性变化差异。研究结果表明:板内温度−应变增量日间变化规律具有明显的滞回特性,且板顶同一点横向温度−应变增量滞回圈面积比纵向的大;板内应力的日间变化具有近似周期性波动特征,波动峰值滞后温度波动峰值约1 h,且任一时间板内同一点纵、横向应力相差不大。板内温度及应变、应力受季节性环境温度影响显著,随环境温度的降低,板内正、负温度梯度的日间交替持续时间有明显变化;板内温度−应变增量滞回圈面积逐渐减小;板顶最大压应力逐渐减小,最大拉应力几乎不受影响。
机场水泥混凝土道面;温度翘曲试验;温度梯度;温度−应力/应变关系
近几十年来,基础设施建设发展迅速,全国乃至全世界范围内的机场修建正处于高速发展阶段[1−2],其中机场道面建设最为重要,它是供飞机飞行前准备、起飞、降落、滑跑、维修保养的重要场地。在气候条件恶劣的地区,机场道面工程修建面临巨大的考验,尤其是机场混凝土道面受温度荷载影响产生的翘曲变形和温度应力是其修建过程中面临的严重问题之一。众多学者对温度荷载作用下水泥混凝土路面的温度翘曲变形及温度应力开展了大量研究,研究方法主要有解析法[3−5]、数值法[6−8]、试验法[9−10]等。解析法能够对所分析问题进行针对性研究,并可得到准确的解析解,然而,对于复杂温度变化或混凝土产生较大变形等问题,解析法的应用往往存在一定困难。数值法能够建立与实际情况相吻合的模型,但为了简化计算,往往进行某些假设,由此造成温度翘曲变形和应力计算值与实测值存在一定的误差。相比而言,试验法的假设和简化条件少,能够更真实地反映混凝土道面板温度翘曲变形和应力变化的实际情况。TELLER等[11]在Arlington试验场对混凝土面层中心的温度分布和温度应力进行研究,验证了板内温度场分布是高度非线性的。CHOUBANE等[12]通过大量的温度实测数据,证明水泥混凝土路面板内温度场沿板厚方向为二次多项式分布。景天然等[13]在同济大学铺筑了水泥混凝土试验路,对温度沿板厚的变化和板顶温度应力进行了研究,结果证明实测温度翘曲应力与威氏法解算结果相近。KIM等[14]基于不同配合比的混凝土路面板温度试验,研究了温度沿板深度的非线性分布特性,结果表明混凝土材料的热导率越小,混凝土板内相应的温差越大。MACKIEWICZ等[15]通过统计欧洲中部地区的温度场非线性分布特征,进一步研究了混凝土道面板内大温差对板内应力分布的影响。田波等[16]通过铺筑足尺试验路,研究了不同基层类型下水泥混凝土路面板中心及板边中心在温度荷载下的响应规律,结果表明贫混凝土基层路面板内温度应力最大,级配碎石基层的最小。颜可珍等[17]基于实测温度非线性分布数据,研究了其对混凝土路面板应力和变形的影响,且提出负温度梯度下板顶最大应力计算公式。魏亚等[18]通过对西南农村地区路面板内温度进行实际测量,分析了路面温度梯度的分布及变化特点,进一步研究了温度梯度和交通荷载的不利组合对不同尺寸路面板的应力影响。综合以上分析,目前,在水泥混凝土路面温度翘曲的试验研究中,针对路面板角内温度场和应力、应变场的关系还缺乏系统和有效的研究。对此,本文作者依托松原查干湖机场混凝土道面工程,基于2016−09—2016−11时间段内板角位置温度、应变监测结果,分析我国东北地区道面板内温度−应力/应变变化关系,以便为我国同地区水泥混凝土道面板的优化设计提供参考。
1 工程背景
1.1 工程概况
松原查干湖机场位于吉林省松原市境内,是1座在建的民用机场。机场场址位于前郭县蒙古艾里乡查干湖村,距松原市区29 km,距查干湖保护区26 km,占地面积1.57×106m2,属于国内支线机场。
1.2 自然气候条件
松原查干湖机场地区属北温带大陆性季风气候。春季干旱少雨,升温较快;夏季炎热,降水集中;秋季凉爽,变温快,温差大;冬季漫长,降雪量小,寒冷干燥。年平均气温为4.5 ℃左右,1月份温度最低,极端最低气温−36.1 ℃;最高气温出现在7月份,极端最高气温37 ℃。2016年该地区9月份和10月份日温差最大,分别达17 ℃和16 ℃。
1.3 机场道面结构
机场跑道长2 500 m,宽45 m,垂直联络道长 233 m,宽23 m。机场道面结构层自上而下依次为:厚度为36 cm的水泥混凝土面层;土工布、透层油;厚度为36 cm的水泥稳定级配碎石基层,分上、下2层,每层厚度为18 cm;厚度为54 cm的级配砂砾石垫层和土基层。水泥混凝土面层标准配合比如表1所示,其物理力学性能参数如表2所示,其中,其含气量(体积分数)为3.4%。

表2 道面混凝土物理力学性能
2 道面温度翘曲现场试验
受环境温度变化影响,水泥混凝土道面板内沿深度方向存在温度梯度,致使板内不同深度层位处发生不均匀的翘曲变形,当板的翘曲变形受板体自重、基层反力、相邻板钳制、面层−基层摩擦、传力杆、拉杆等因素的约束作用时板内不同位置将分别产生拉、压应变。基于此,本文作者通过在松原查干湖机场现浇混凝土道面板内埋设温度和应变传感器监测板角温度和应变变化情况。
2.1 试验道面板块选取
松原查干湖机场道面板分块纵向为5.0 m,横向为4.5 m。由于温度和应变传感器埋设于机场道面内,为避免对道面施工质量和后期运行造成影响,选择机场跑道纵向中间位置最外侧某一板块作为试验板块。为分析道面板角位置温度及温度−应变变化,温度和应变传感器埋设于道面板角位置。
2.2 传感器布设
根据MH/T 5004—2010“民用机场水泥混凝土道面设计规范”规定:机场跑道钢筋混凝土板设计中钢筋保护层厚度不应小于50 mm。因此,现场试验埋设温度、应变传感器时,道面板顶和板底混凝土保护层厚度预留60 mm。
试验道面板角温度传感器沿竖向自上而下每隔 8 cm布设1个,共布设4个;应变传感器分别于板顶、板底各布设2个,1个沿板纵向布置、1个沿板横向布置,共布设4个。道面板内温度、应变传感器平面及竖向布置图如图1所示,图1中:A1为温度传感器;B1为纵向应变传感器;C1为横向应变传感器;A1−1/2/3/4为温度传感器自上而下布设编号;B1−1/2为板顶、板底纵向应变传感器的编号;C1−1/2为板顶、板底横向应变传感器的编号。
2.3 数据采集
现场试验采用长沙金码公司生产的埋入式JMT−36B半导体温度计和JMZX−215A智能应变计自动采集道面板内温度和应变。数据传输及存储采用JMTX−2014无线传输模块和DSC软件系统。试验道面板块浇筑时间为2016−09−03T6:00,温度、应变 采集时间为2016−09−03—2016−11−03,采集间隔为 1次/h。
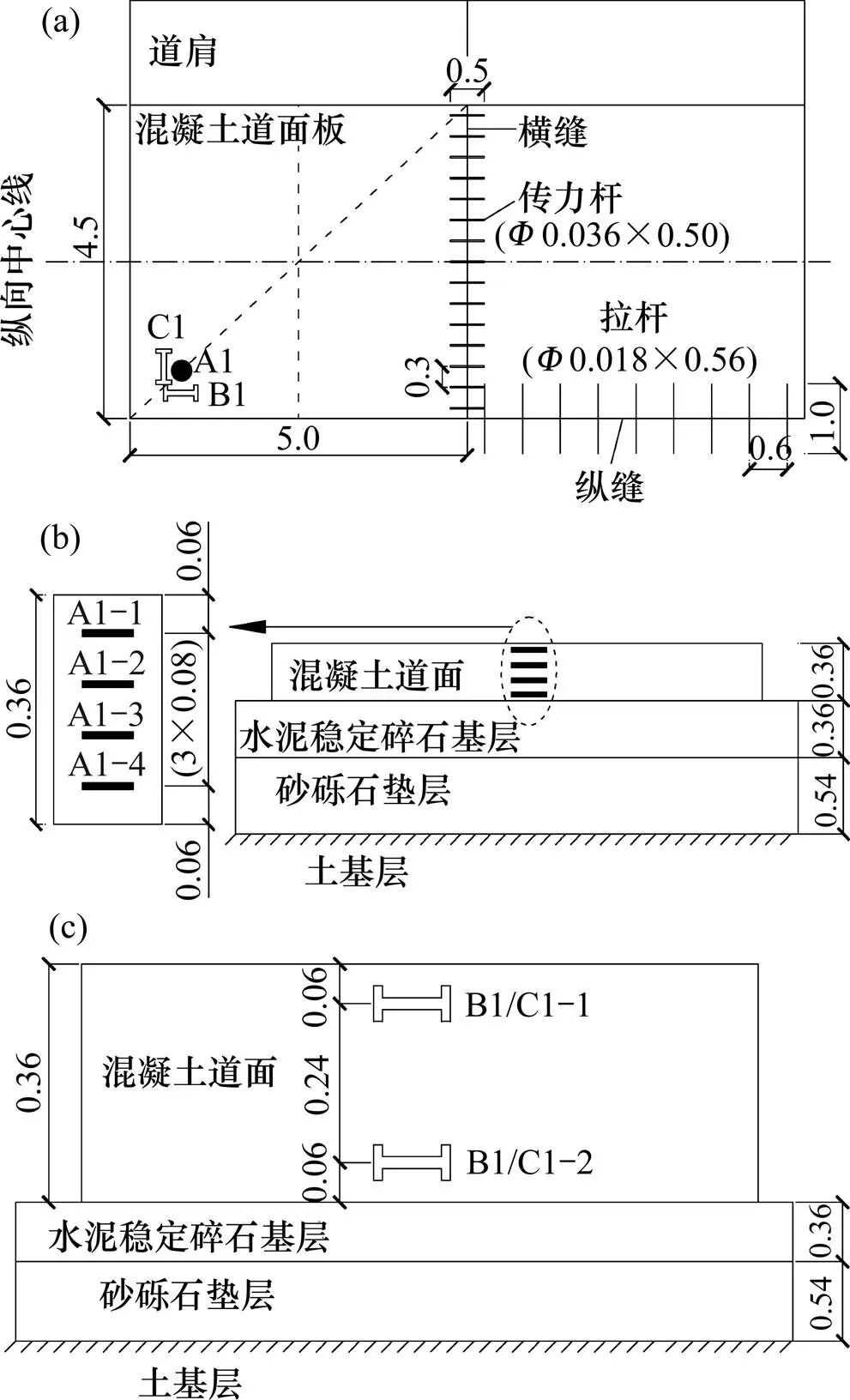
数据单位:m
3 试验结果分析
3.1 温度场长期分布规律
选取观测周期内每日3:00和15:00的温度,得到试验道面板角处温度随时间的长期变化情况,如图2所示。东北地区自9月份至11月份,受季节影响环境温度逐渐下降。从图2可以看到:受环境温度变化的影响,道面板内温度呈逐渐下降趋势;在同一时间,因道面自身板厚的原因,板内温度沿板厚度方向呈明显的梯度分布:夜晚(3:00)板顶温度低于板底温度,板内为负温度梯度;白天(15:00)板顶温度高于板底温度,板内为正温度梯度,且板内温度梯度不受季节影响,温度梯度一直存在。
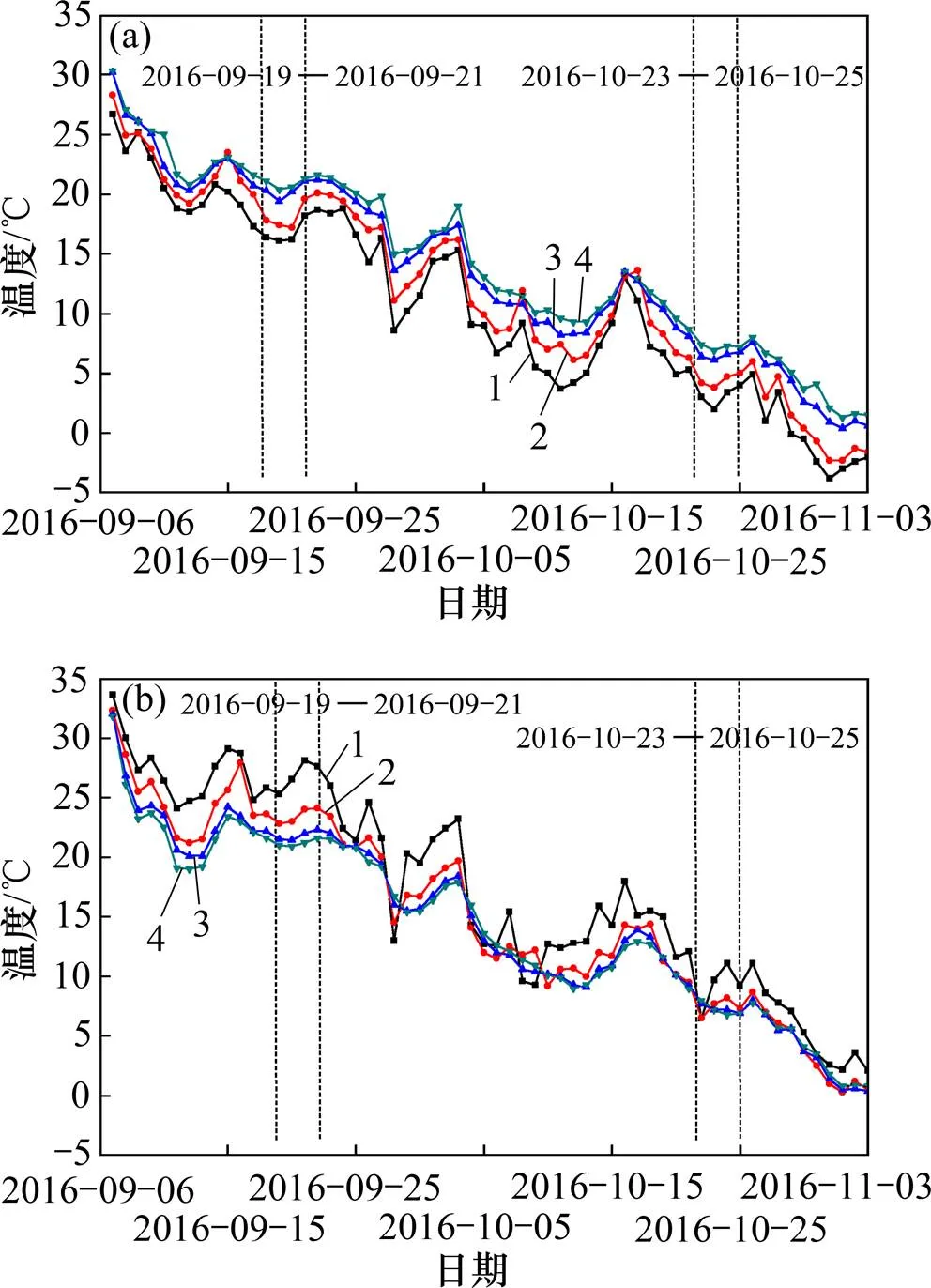
时刻:(a) 3:00;(b) 15:00
3.2 温度场日间分布规律
为研究板角温度梯度受季节性环境温度的影响规律,选取9月份中旬与10月份下旬2个时间段进行分析,具体为2016−09−19—2016−09−21和2016−10− 23—2016−10−25。在该时间段内,当地天气晴朗时,白天光照强烈,受地域特点影响,夜晚温度低,昼夜温差变化大,其温度变化特点具有代表性。且从图2可以看到:在2个时间段内,板内正、负温度梯度明显。因季节性环境温度差异,9月份与10月份2个时间段内环境温度相差约15 ℃。试验板角温度日间波动曲线如图3所示,不同时间板角温度随深度变化曲线如图4所示。
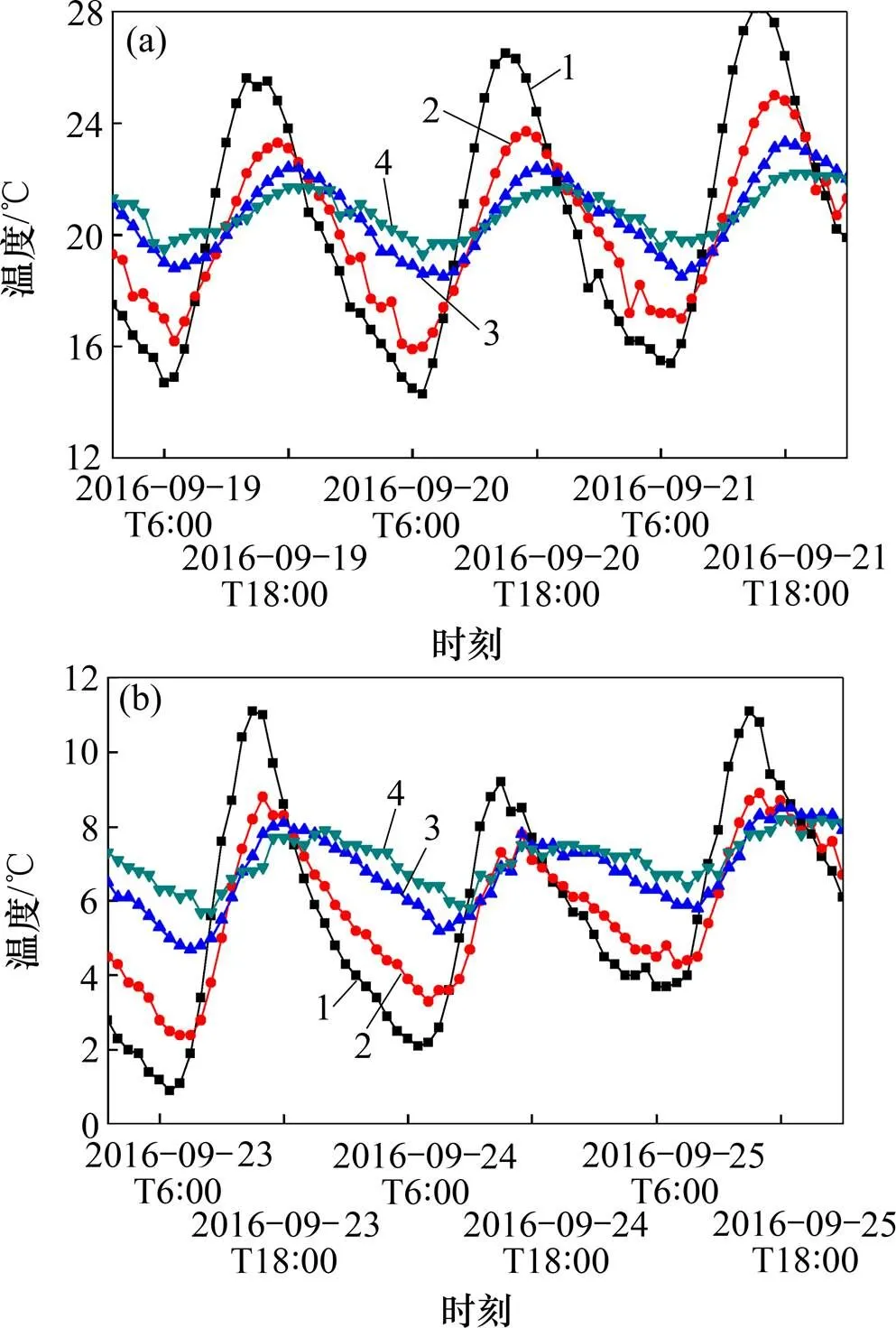
(a) 2016−09−19—2016−09−21;(b) 2016−10−23—2016−10−25
从图3可以看出:板内温度日间波动曲线随时间呈近似周期性波动,波动周期为24 h。板顶温度受环境温度影响最为显著,波动最为剧烈,板内温度波动幅度随着板深度增加逐渐减小,相位也依次滞后。受季节性环境温度影响,东北地区不同月份某天板内正、负温度梯度持续的时间不同,9月份某天板内正温度梯度持续时间约为10 h (10:00—20:00),负温度梯度持续时间约为14 h;10月份某天内板内正温度梯度持续时间约为7 h (11:00—18:00),负温度梯度持续时间约为17 h。由此可知:随季节性环境温度的降低,板内正温度梯度持续的时间逐渐缩短,负温度梯度持续的时间逐渐延长。
从图4可以看出:板内温度在板深度方向呈明显的非线性分布,且在1 d之内不同时间变化较大,板内不同深度层位间存在温度梯度,且随着深度增加,温度的变化趋势越来越小,板的上半层温度梯度远比下半层的大。东北地区不同月份某天板顶、板底最大正、负温度梯度发生的时间相同,1 d内最大正温度梯度出现在15:00,最大负温度梯度出现在6:00;但正、负温度梯度相差较大,9月份最大正温度梯度为7.2 ℃,最大负温度梯度为−5.6 ℃;10月份最大正温度梯度为5.1 ℃,最大负温度梯度为−6.5 ℃。由此可得:随季节性环境温度的降低,板内正温度梯度逐渐减小,而负温度梯度逐渐增大。
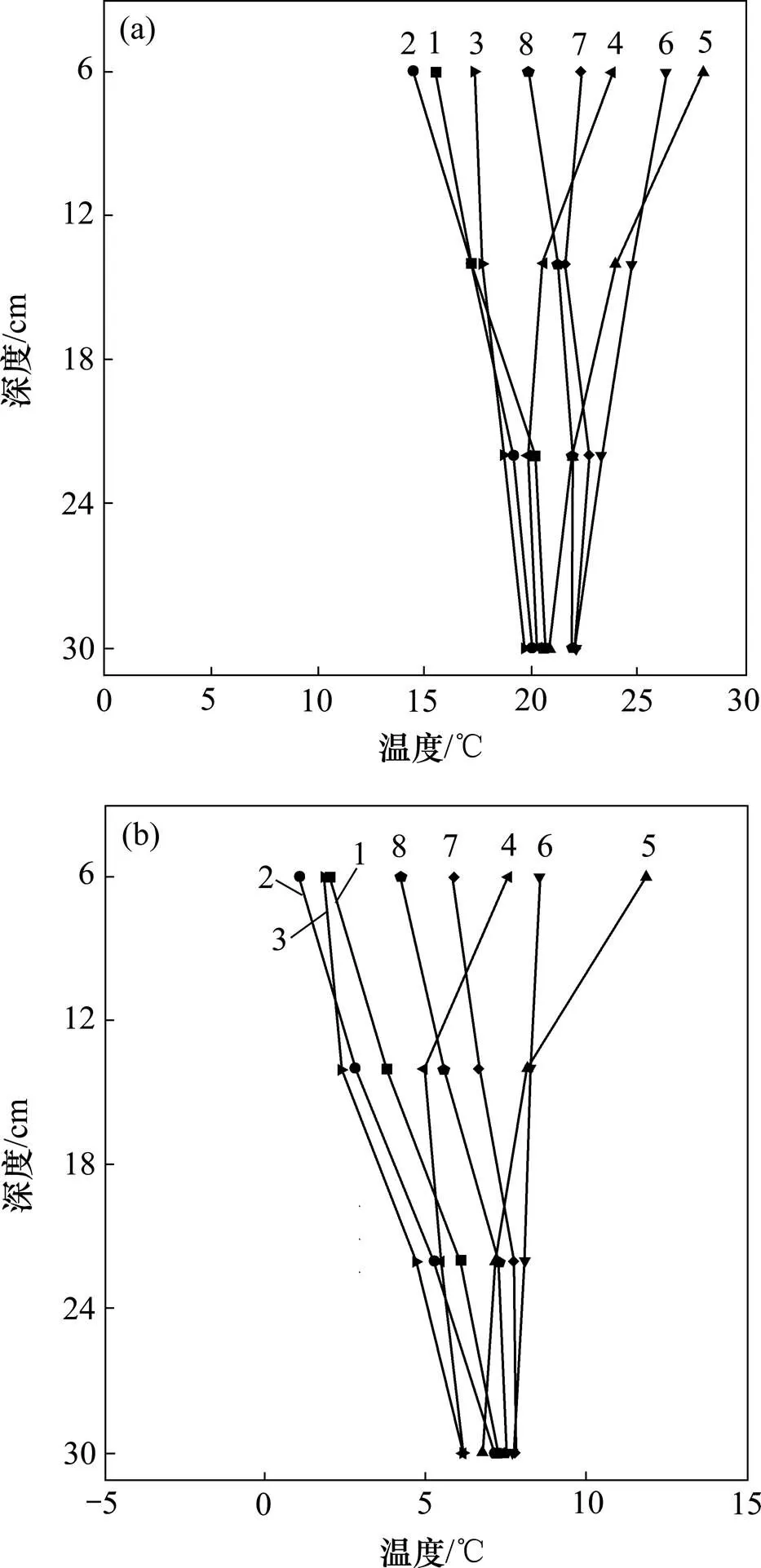
(a) 2016−09−20;(b) 2016−10−23
3.3 应变分析
为了分析板角温度与应变增量的关系,选取温度最为均匀(温度梯度几乎为0 ℃)的时间作为温度和应变数据的基准值,其他时间的温度、应变均为相对于基准值的温度增量和应变增量。若忽略固化翘曲、干缩翘曲、徐变等效应的影响,则板在基准时间应平整,且与基层保持完全接触的状态。从图3可以看到本文试验研究数据处理的基准时间:9月份为每日10:00和20:00,10月份为每日11:00和18:00。基准值为 2个时间温度或应变的平均值,板内实测温度−应变增量滞回曲线如图5、图6所示。
从图5、图6可以看出:混凝土板内温度−应变增量曲线表现出非常明显的滞回效应,即应变随温度升高或降低的变化路径并不重合,而是形成1个滞回圈,且日间的温度−应变增量滞回圈不完全重合;1 d内板顶温度−应变滞回圈面积明显比板底的大,即板顶滞回圈的长、短轴更大;1 d内板顶同一点纵、横向温 度−应变增量滞回圈面积也不相同,其表现为滞回圈的长轴相同,短轴不同,即同一点的温度增量相同,但横向应变增量大于纵向增量;1 d内板底同一点纵、横向温度−应变增量滞回圈面积相差不大。
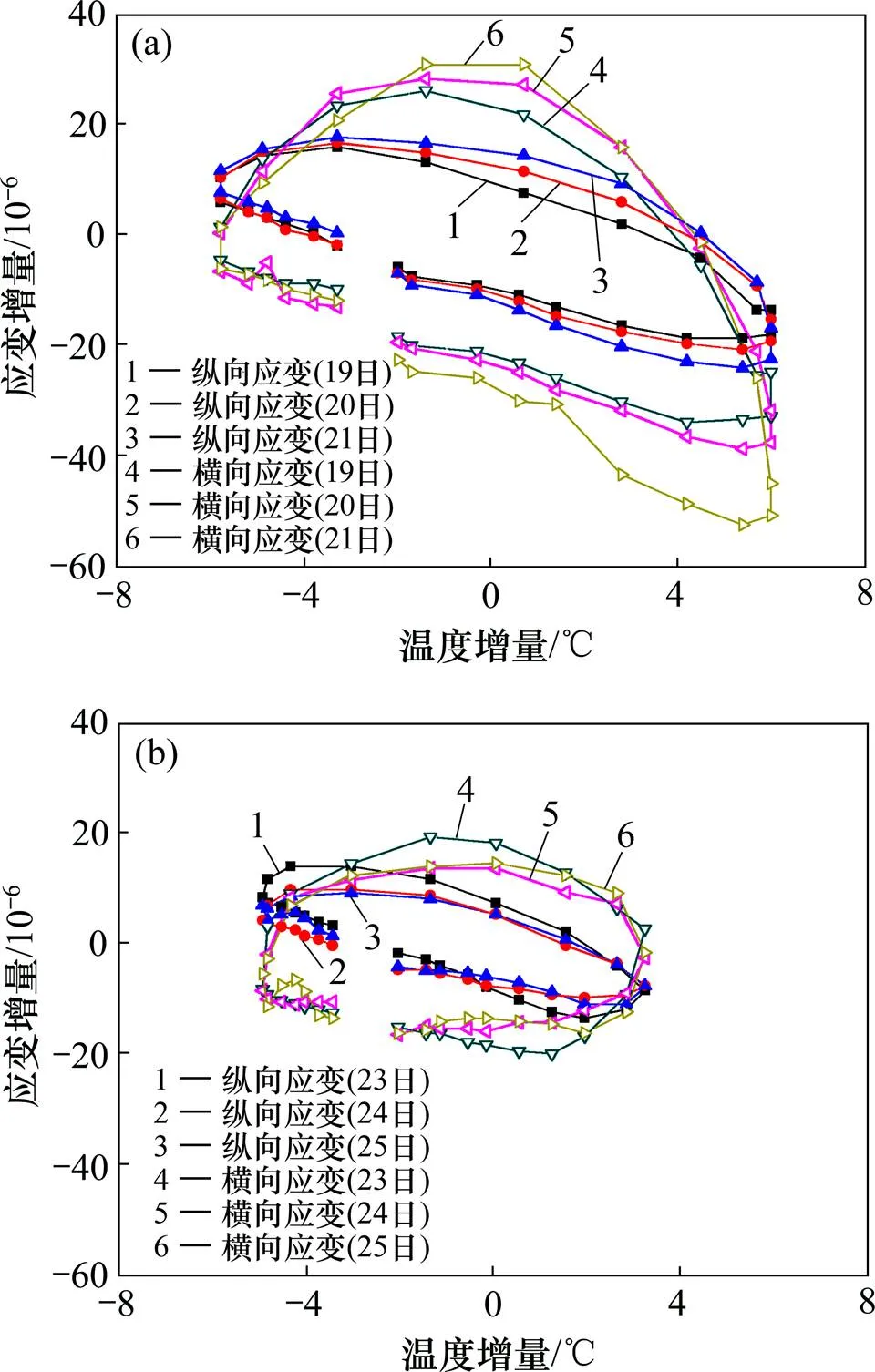
(a) 2016−09−19—2016−09−21;(b) 2016−10−23—2016−10−25

(a) 2016−09−19—2016−09−21;(b) 2016−10−23—2016−10−25
分析东北地区不同月份的温度−应变增量对比可得:受季节性环境温度影响,不同月份板内(板顶或板底)温度−应变增量滞回圈面积不同,与10月份相比,9月份明显更大。因此,可以得出随季节性环境温度的降低,板内温度−应变增量滞回圈面积逐渐减小。
3.4 应力分析
文献[19]指出,根据弹性薄板理论,考虑温度效应的影响,混凝土板内应力可通过下式计算:


试验道面板角纵、横向应力随时间的波动曲线如图7所示,以拉应力为正。
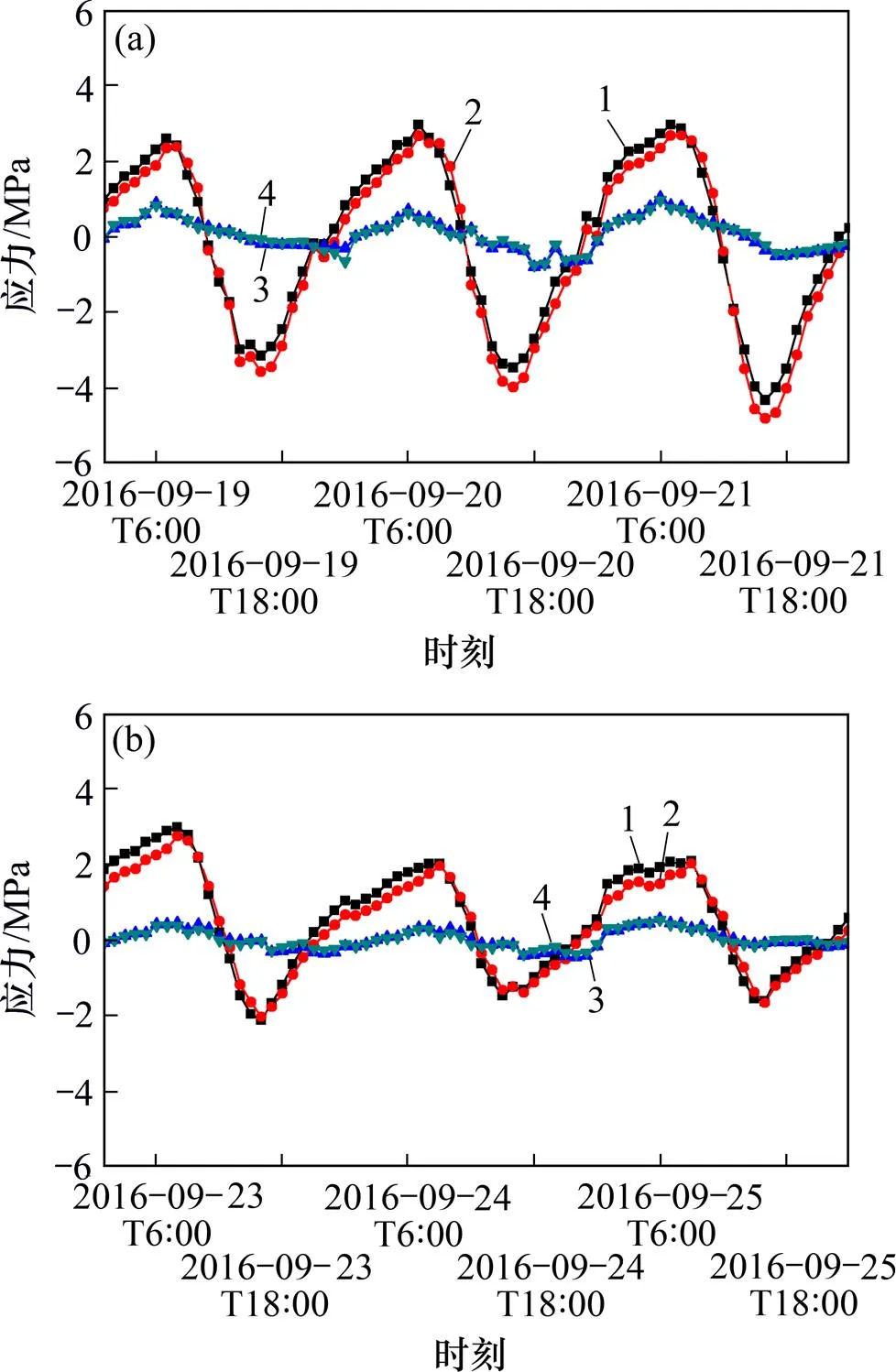
(a) 2016−09−18—2016−99−20;(b) 2016−10−23—2016−10−25
从图7可以看到:考虑温度效应的板内应力随时间变化呈近似周期性波动,波动周期为24 h,板顶内应力周期性波动更明显;板顶或板底同一点纵、横向应力随时间变化的波动趋势相吻合,当板顶为拉应力时,纵向拉应力稍大于横向拉应力,最大仅相差 0.48 MPa,当板顶为压应力时,纵、横向压应力相当或横向压应力稍大,最大仅相差−0.59 MPa;板底纵、横向拉压应力相差不大,拉应力最大相差0.09 MPa,压应力最大相差−0.11 MPa。
对比分析东北地区不同月份的板内应力可得:板顶拉应力相差较小,压应力相差较大;板底拉压应力均相差较小。9月份与10月份板顶最大拉应力分别为2.96 MPa和2.99 MPa,最大压应力分别为−4.8 MPa和−2.13 MPa;9月份与10月份板底最大拉应力分别为0.79 MPa和0.56 MPa,最大压应力分别为 −0.74 MPa和−0.47 MPa。因此,可以得出:随季节性环境温度的降低,板底拉压应力变化较小,板顶最大拉应力变化不大,但最大压应力逐渐减小。
综合分析图4和图8可知:当板角为负温度梯度时,板顶为拉应力;当板角为正温度梯度时,板顶为压应力。1 d内板顶最大拉压应力发生的时间滞后于最高、最低温度发生时间,板顶最低温度发生在6:00—7:00,最大拉应力发生在7:00—8:00,板顶最高温度发生在14:00—15:00,最大压应力发生在15:00—16:00,即1 d内板顶应力波动峰值滞后于温度波动峰值约1 h。
4 结论
1) 混凝土板内温度受季节性环境温度影响显著,板内温度与环境温度变化趋势相吻合。且随季节性环境温度降低,板内正温度梯度持续的时间逐渐缩短,最大正温度梯度逐渐减小,负温度梯度持续的时间逐渐延长,最大负温度梯度逐渐增大。
2) 混凝土板内温度沿深度方向非线性分布和日间非完全周期性波动的特性,使板内温度−应变增量曲线表现出非常明显的滞回效应,且日间的温度−应变增量滞回圈不完全重合。1 d内板顶同一点横向温度−应变增量滞回圈比纵向的大;但板底同一点纵、横向温度−应变增量滞回圈相差不大。且随季节性环境温度的降低,板内温度−应变增量滞回圈面积逐渐 减小。
3) 考虑温度效应的板内应力随时间日间变化呈近似周期性波动,板顶波动显著,板底波动较弱,1 d内板顶应力波动峰值滞后温度波动峰值约1 h。板内同一点纵、横向应力随时间日间变化的波动趋势相吻合,任一时间纵、横向应力相差不大:板顶纵、横向最大拉应力相差0.48 MPa,最大压应力相差−0.59 MPa;板底纵、横向拉应力最大相差0.09 MPa,最大压应力相差−0.11 MPa。且随季节性环境温度降低,板底拉压应力变化较小,板顶最大压应力逐渐减小,但最大拉应力几乎不受影响。
[1] 蔡靖, 李岳, 孙钦刚. 温度场下的机场柔性道面转弯区轮辙规律研究[J]. 西南交通大学学报, 2017, 52(1): 186−194. CAN Jing, LI Yue, SUN Qingang. Rutting behavior of flexible pavement in airport turning area under temperature field[J]. Journal of Southwest Jiaotong University, 2017, 52(1): 186−194.
[2] 靳美倩. 机场水泥混凝土道面典型病害分析及处治技术研究[D]. 西安: 长安大学材料科学与工程学院, 2015: 1−15.
JIN Meiqian. Research on typical diseases analysis and treatment technology of airport cement concrete pavement[D]. Xi’an: Chang’an University. School of Materials Science and Engineering, 2015: 1−15.
[3] WESTERGAARD H M. Analysis of stresses in concrete pavements caused by variation of theoretical[J]. Highway Research Board Proceedings, 1927, 6: 201−205.
[4] 姚祖康. 水泥混凝土路面的温度翘曲应力[J]. 同济学学报(自然科学版), 1981(3): 44−54. YAO Zukang. Thermal warping stress in concrete pavements[J]. Journal of Tongji University(Natural Science Edition), 1981(3): 44−54.
[5] 谈至明, 姚祖康. 非线性温度场下的水泥混凝土路面温度应力[J]. 中国公路学报, 1993, 6(4): 9−17. TAN Zhiming, YAO Zukang. Thermal stress in cement concrete pavements with non-linear temperature regime[J]. China Journal of Highway and Transport, 1993, 6(4): 9−17.
[6] 张君, 祁锟, 张明华. 早龄期混凝土路面板非线性温度场下温度应力的计算[J]. 工程力学, 2007, 24(11):136−145.
ZHANG Jun, QI Kun, ZHANG Minghua. Calculation of the thermal stresses in concrete pavement at early ages[J]. Engineering Mechanics, 2007, 24(11): 136−145.
[7] 权磊, 田波, 冯德成, 等. 水泥混凝土板硬化温度翘曲正向计算方法研究[J]. 土木工程学报, 2016, 49(4): 121−128. QUAN Lei, TIAN Bo, FENG Decheng, et al. Forward calculation method to determine built-in thermal curling of concrete slabs[J]. China Civil Engineering Journal, 2016, 49(4): 121−128.
[8] KIM S H, PARK J Y, JEONG J H. Effect of temperature-induced load on airport concrete pavement behavior[J]. KSCE Journal of Civil Engineering, 2014, 18(1): 182−187.
[9] 徐庆元, 孟亚军, 李斌, 等. 温度梯度作用下纵连板式无砟轨道疲劳应力谱[J]. 中南大学学报(自然科学版), 2015, 46(2): 736−741.XU Qingyuan, MENG Yajun, LI Bin, et al. Fatigue stress spectrum of longitudinally connected ballastless track under temperature gradient[J]. Journal of Central South University(Science and Technology), 2015, 46(2): 736−741.
[10] DULCE R, JEFFERY R. Effects of temperature curling on airfield rigid pavement responses[J]. Road Materials and Pavement Design, 2005, 6(3): 311−337.
[11] 李永毅, 李强, 吴士斌, 等. 高温差下混凝土板温度翘曲试验研究[J]. 低温建筑技术, 2014, 36(12): 12−14. LI Yongyi, LI Qiang, WU Shibin, et al. Experimental research on temperature warping of concrete slabs under high temperature difference[J]. Low Temperature Architecture Technology, 2014, 36(12): 12−14.
[12] NAM B H, YEON J H, BEHRING Z. Effect of daily temperature variations on the continuous deflection profiles of airfield jointed concrete pavements[J]. Construction and Building Materials, 2014, 73: 261−270.
[13] CHOUBANE B, TIA M. Analysis and verification of thermal-gradient effects on concrete pavement[J]. Journal of Transportation Engineering, 1995, 121(1): 75−81.
[14] KIM K, CHUN S. Evaluation of internally cured concrete pavement using environmental responses and critical stress analysis[J]. International Journal of Concrete Structures & Materials, 2015, 9(4): 463−473.
[15] MACKIEWICZ P. Thermal stress analysis of jointed plane in concrete pavements [J]. Applied Thermal Engineering, 2014, 73(1): 1169−1176.
[16] 田波, 权磊, 牛开民. 不同基层类型水泥混凝土路面温度翘曲结构试验与理论分析[J]. 中国公路学报, 2014, 27(6): 17−26. TIAN Bo, QUAN Lei, NIU Kaimin. Structural experiment and theoretical analysis of thermal curling in JPCP with different base types[J]. China Journal of Highway and Transport, 2014, 27(6): 17−26.
[17] 颜可珍, 沈光辉, 游凌云. 非线性温度梯度作用下水泥混凝土路面力学分析[J]. 湖南大学学报(自科版), 2015, 42(7): 74−80.
YAN Kezhen, SHEN Guanghui, YOU Lingyun. Mechanical analysis of cement concrete pavement on nonlinear temperature profile[J]. Journal of Hunan University(Natural Sciences), 2015, 42(7): 74−80.
[18] 魏亚, 梁思明, 和昆, 等. 温度与荷载耦合下农村公路混凝土路面板结构尺寸优化[J]. 工程力学, 2015, 32(7): 111−117. WEI Ya, LIANG Siming, HE Kun, et al. Slab-size optimization of rural road concrete pavement considering the combined effect of temperature gradient and traffic load[J]. Engineering Mechanics, 2015, 32(7): 111−117.
[19] 铁摩辛柯S, 沃诺斯基S. 板壳理论[M]. 《板壳理论》翻译组, 译. 北京: 科学出版社, 1977: 171−177. TIMOSHENKO S, WOINOWSKY-KRIEGER S. Theory of plates and shells[M]. Theory of plates and shells translation teams, trans, Beijing: Science Press, 1977: 171−177.
(编辑 刘锦伟)
Experimental research on temperature warping of airport cement concrete pavement in northeast China
ZHANG Wanzhi1, XU Bangshu1, LI Bing1, YANG Laihua2, LIAN Yanwu2
(1. Geotechnical and Structural Engineering Research Center, Shandong University, Jinan 250061, China; 2. China Railway 12th Bureau Group Co. Ltd., Taiyuan 030024, China)
In order to study the temperature distribution and temperature-stress/strain relationship of concrete slab corner of airport pavement in northeast China, a pavement temperature warping experiment was carried out based on the Chagan Lake Airport Pavement Project under construction. Daily and seasonal variations of temperature, strain and stress at different depths of concrete slab corner were constantly monitored by intelligent temperature-strain sensors. The results show that the daily variations of the temperature-strain increment in the lab have obvious hysteretic-like characteristics, and the transverse temperature-strain increment hysteresis loops are larger than those in the longitudinal direction in the sameposition on the top of the slab. Daily variations of the stress in the slab are characterized by approximate periodic fluctuation; However, the wave peaks of the stress lag behind the temperature about an hour. Meanwhile, there is little difference between the longitudinal and transverse stresses in the slab at the same time and in the same position. The temperature, strain and stress in the slab are significantly influenced by the seasonal environment temperature. With the decrease of the environment temperature, the daily alternating durations of the positive and negative temperature gradients in the slab vary accordingly, and the temperature-strain increment hysteresis loops shrink gradually. Simultaneously, the maximum compressive stress on the top of the slab decreases, but the maximum tension stress are hardly affected.
airport cement concrete pavement; temperature warping experiment; temperature gradient; temperature− stress/strain relationship
10.11817/j.issn.1672-7207.2018.09.025
U416.216
A
1672−7207(2018)09−2308−08
2017−09−12;
2017−11−15
国家自然科学基金资助项目(50909056);山东省自然科学基金资助项目(ZR2014EEM029,ZR2014EEM014);住房城乡建设部2015年科学技术项目(2015-K5-004) (Project(50909056) supported by the National Natural Science Foundation of China; Projects (ZR2014EEM029, ZR2014EEM014) supported by the Natural Science Foundation of Shandong Province; Project(2015-K5-004) supported by the 2015 Science and Technology Program of the Housing and Urban-Rural Construction Ministry)
徐帮树,博士,副教授,从事道路工程安全及GIS软件系统开发与应用研究;E-mail: xubangshu@sdu.edu.cn
