肋梁−桩−锚支护结构锚索拉力计算理论模型及其应用
2018-10-13尹泉傅鹤林刘运思岳健郭志广
尹泉,傅鹤林,刘运思,岳健,郭志广
肋梁−桩−锚支护结构锚索拉力计算理论模型及其应用
尹泉1, 2,傅鹤林1,刘运思3, 4,岳健3, 4,郭志广4
(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 湖南城市学院 土木工程学院,湖南 益阳,413000;3. 湖南科技大学 岩土工程稳定控制与健康监测省重点实验室,湖南 湘潭,411201;4. 湖南科技大学 土木工程学院,湖南 湘潭,411201)
肋梁−桩−锚支护结构有别于传统桩锚支护结构,前者在传统排桩上增设了竖向肋梁。为解决肋梁桩锚支护结构中锚索拉力计算问题,以变形协调理论为基础,根据肋梁、桩和锚索这3种支护结构在共点时水平位移相等,构建肋梁−桩−锚索共同支护作用下锚索拉力计算理论模型,并将该模型应用于某深基坑工程的锚索拉力计算。研究结果表明:基于该理论模型求解得到的锚索拉力小于传统桩锚支护结构锚索拉力,与工程实际结果更加接近;由于有肋梁存在,支护结构整体刚度提高,支护结构的受力分布更加合理,锚索内力更小,节约了工程造价,同时提高了支护结构的整体稳定性。
深基坑支护;变形协调;肋梁−桩−锚支护;锚索拉力;刚度;稳定性
随着城市超高层建筑的发展,深基坑支护结构设计面临巨大挑战。目前,桩锚支护结构是深基坑最常见的支护形式之一,桩锚支护体系的受力和变形分析是深基坑建设中非常重要的研究课题[1−6]。如何准确计算锚索拉力是桩锚支护结构设计的关键问题,在一般情况下,桩锚支护结构通过考虑锚索与桩的变形协调求解[7−9]。如刘焕斌等[10]提出了一种确定预应力的方法,将锚索、抗滑桩与周围的岩土体作为一个整体,根据桩身正负弯矩基本相等时锚索上的拉力视为总拉力,再充分考虑桩锚协调变形条件进行锚索预应力计算。晏鄂川等[11]在此基础上对变形协调方程从2个方面进行改进,考虑了预应力施加完成后和桩后土压力逐步作用在抗滑桩上这2个阶段桩体变形协调,同时也考虑了其他排锚索作用效果对变形协调的影响,这样更加接近实际情况。简文星等[12]则对常规和修改变形协调条件再次进行优化,优化的变形协调不仅能使抗滑桩在预应力施加阶段处于有利的受力和变形状态,而且适用于锚索与水平面成不同角度的情况。可见,许多学者针对桩锚支护结构锚索预应力以及总应力进行了研究[13−15],但针对加设肋梁的桩锚支护结构的研究较少,而该种支护形式已应用于工程实践中,如长沙国际金融中的35 m深基坑便采取了该种支护形式。人们对类似的圈梁、腰梁与桩锚共同支护的框架结构有少量研究,如孙书伟等[16]进行了对框架微型桩结构抗滑特性的模型试验,发现框架梁可以有效限制微型桩顶位移并减小桩身弯矩,但也会在微型桩顶部产生较大的弯矩。胡敏云等[17]认为圈梁对护壁桩顶的约束作用随桩身变形的发展而变化,两者协同工作有利于减小桩身内力,提高护壁桩的安全性,并提高排桩支护的整体稳定性。设计时,应计入圈梁的有利影响,以使基坑支护安全、合理且经济。钱同辉等[18]研究了框架式抗滑桩受力特性,发现纵、横向框架梁与桩的连接对框架式抗滑桩起到了支点作用,有效地抑制了最大位移的增加,改变了桩和锚索的内力。基于此,本文作者以变形协调理论为基础,根据肋梁、桩和锚索3种支护结构在共点时水平位移相等,推导肋梁−桩−锚索共同支护作用下锚索拉力的求解公式。
1 桩锚变形协调方程
1.1 桩锚变形协调基本假设
1) 不考虑桩体自身重力、桩体反力、桩与土体的摩擦力的作用,假设滑动面桩体背后土压力荷载为三角形分布。
2) 在研究锚索受力时,将桩与锚索共同作用点考虑为弹性铰支座,在进行滑动面以上部分的桩与锚索受力分析时按结构静力学原理计算。
3) 考虑桩与锚索间的变形协调时,锚索伸长量在水平方向的分量与锚索作用于桩处的水平位移相等。
1.2 计算模型

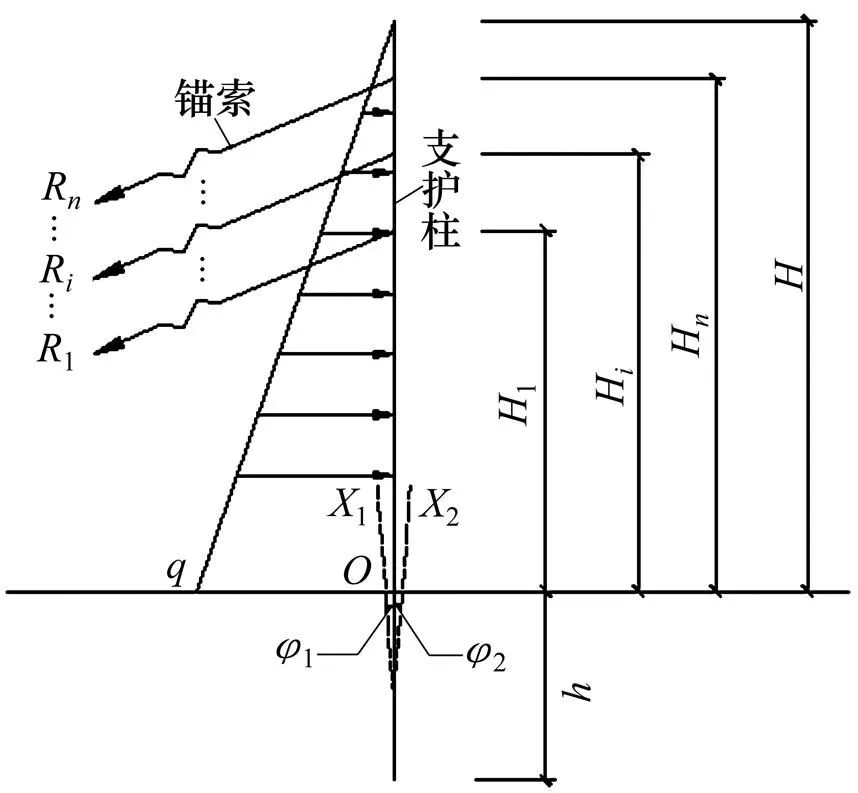
图1 桩−锚结构计算简图
假设基坑开挖面以上主动土压力呈三角形分布,则按朗肯土压力计算:
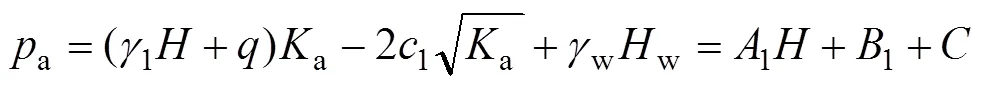
对于基坑内底部以下的土体,在嵌入支护桩后的土压力仍可按朗肯主动土压力计算,而嵌入支护桩前部的土体则受到被动土压力,可按朗肯被动土压力计算式表示为
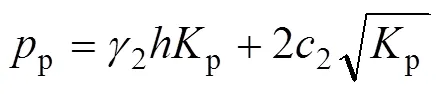

1.3 桩锚变形协调
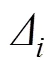
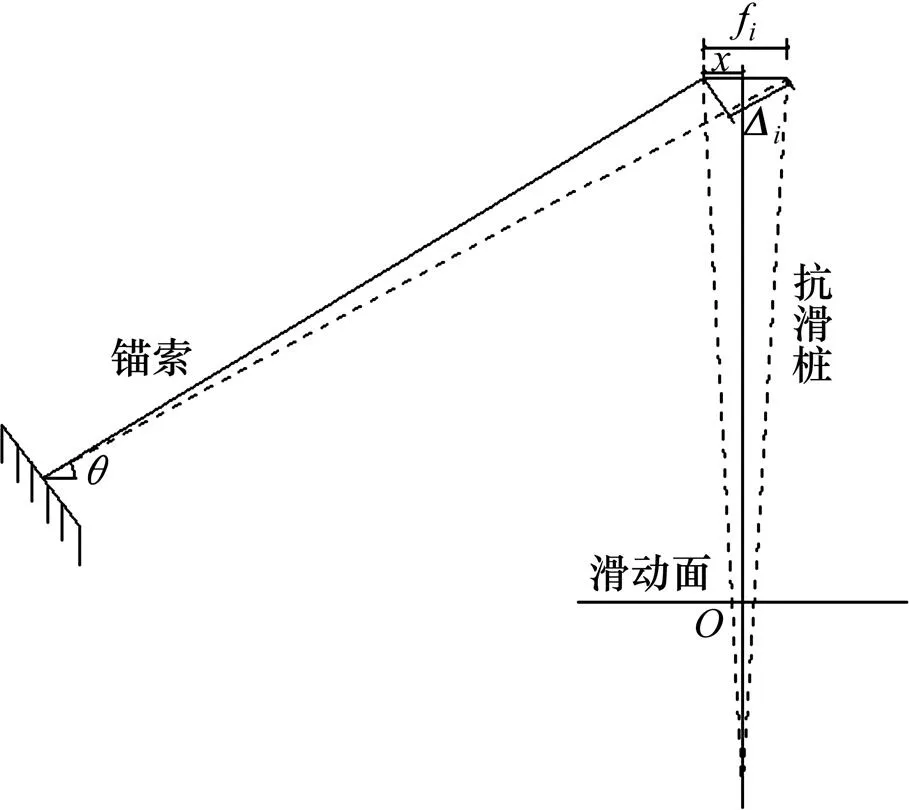
图2 桩锚变形协调示意图
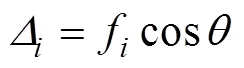
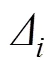
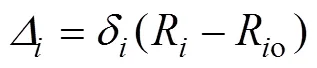

锚索作用点处桩的水平位移f为
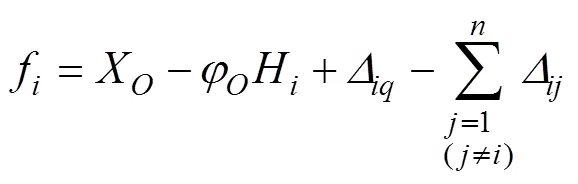

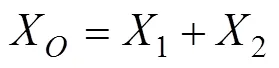
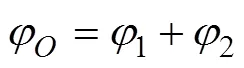
根据地基系数法,预应力锚索产生的位移1为
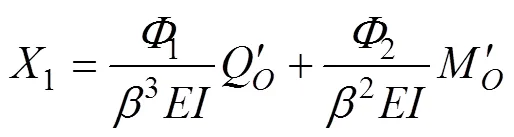

其中,
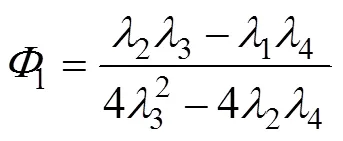

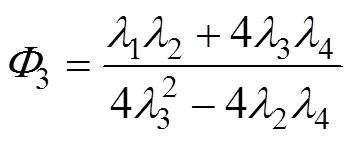
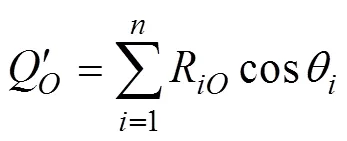
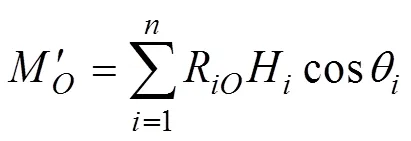

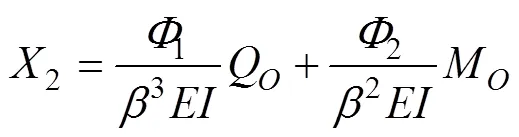

式中:Q和M为桩后土压力和锚索应力在锚固段顶端点处的剪力和弯矩。

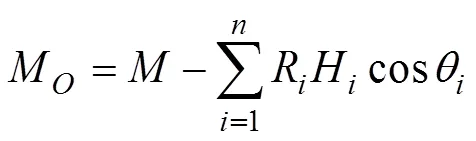
式中:和分别为土压力作用于桩嵌固端顶端点的剪力和弯矩,根据桩后土压力分布和郎肯土压力计算公式,有
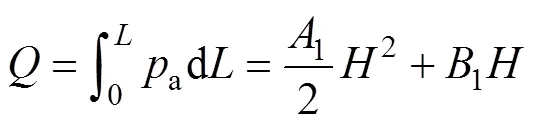



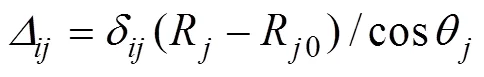

2 肋梁与桩锚支护结构变形协调理论
2.1 肋梁与桩锚变形协调基本假设
1) 不考虑肋梁和桩的自重、桩与土体的摩擦力作用,假设肋梁上受土压力为分布荷载,锚索拉力为集中力;
2) 肋梁按Winkler地基模型有限长梁计算;
3) 考虑肋梁与桩相交的节点处变形协调,肋梁与桩相交节点处肋梁水平挠度与该处桩水平位移相等。
2.2 计算模型
肋梁与桩相交的节点处作用锚索拉力为1,…,R,…,R,肋梁长度为,锚索与锚索之间的距离为,锚索拉力1与肋梁边缘距离为,则计算模型如图3所示。
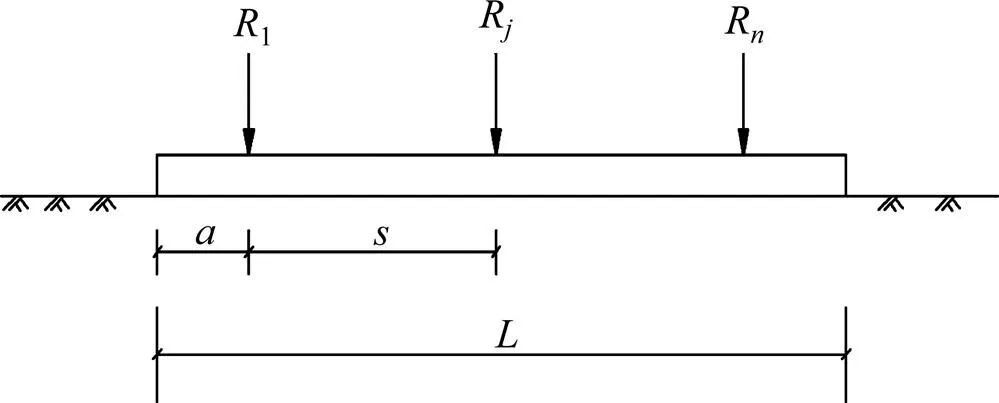
图3 肋梁计算简图
在Winkler地基模型基础上,将图3分解成若干个受集中力下的有限长梁,其受力模型如图4所示。
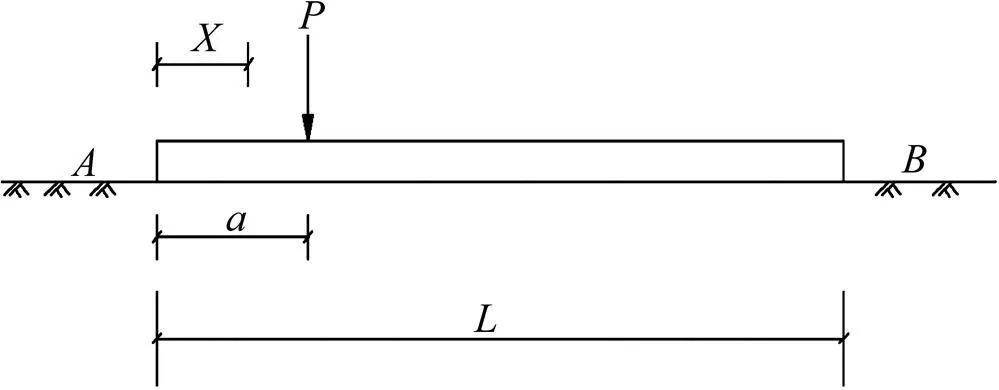
图4 集中力作用下有限长梁计算模型
有限长梁作用集中力时的挠度方程如下。
当<时,


当<<时,
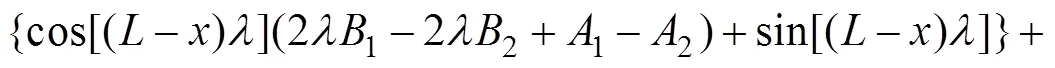


对于多个集中力作用下的有限长梁扰度问题,可采用叠加法计算,即
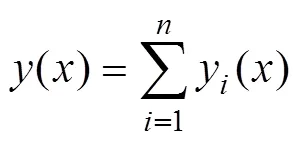
2.3 肋梁与桩锚变形协调
肋梁、桩和锚索共点处变形相等,其肋梁的水平方向挠度与桩水平方向变形以及锚索伸长量的水平分量相等,有

将肋梁、桩和锚索共点处视为1个节点,每个节点包含2个未知量R和R,分别为实际工作状态时的总拉力和锚索初始预拉力。根据肋梁桩锚变形协调即式(29),每个节点可列出3个平衡方程,将所有节点考虑进来,未知力数目小于平衡方程数目方可求解所有节点处的锚索拉力R和R。
3 算例分析
长沙国际金融中心基坑工程位于长沙市黄兴路与蔡锷路之间、解放西路以北、东牌楼街以南。拟建建筑物最大高度为452.00 m,基坑深度=34.25 m。采用肋梁桩锚支护结构,共设12排锚索,锚索倾角为15°,支护桩的直径为1.80 m,间距为2.40 m,其基坑典型计算简图如图5所示。
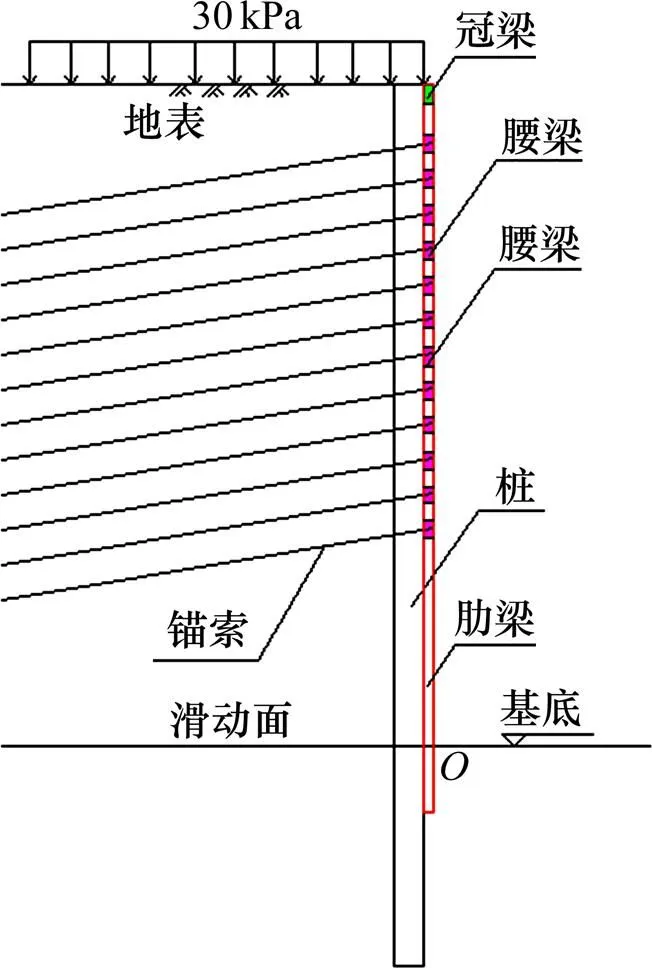
图5 肋梁桩锚支护计算简图
根据朗肯土压力理论,计算作用在支护结构上的土压力为15 900 kN/m,桩长=44.0 m,悬臂端= 34.0 m,嵌固端=10.0 m,每排锚索距坑底的距离为1=31.5 m,2=29.0 m,3=27.0 m,4=25.0 m,5= 23.0 m,6=21.0 m,7=19.0 m,8=17.0 m,9=15.0 m,10=13.0 m,11=11.0 m,12=9.0 m;每排锚索的自由端分别为1=21.0 m,2=20.0 m,3=18.0 m,4=17.0 m,5=16.0 m,6=15.0 m,7=14.0 m,8=13.0 m,9=12.0 m,l10=10.0 m,11=8.0 m,12=7.0 m;锚索孔径为200.0 mm,内置预应力钢绞线,锚索倾角为15°,肋梁截面面积为0.5 m×0.5 m,腰梁截面面积为0.8 m×0.8 m,桩身和肋梁材料采用C30混凝土。

4 结论
1) 以变形协调理论为基础,将肋梁视为Winkler地基模型上的有限长梁,推导了肋梁−桩−锚索共同支护作用下锚索工作应力和预应力的解析解。
2) 考虑肋梁影响时的锚索拉力要比不考虑肋梁时的小。
3) 肋梁的存在提高了支护结构的整体刚度,有效地减小了基坑的变形。
[1] 周诚, 蒋双南, 林兴贵. 基于无人机的深基坑施工安全风险巡视与预警研究[J].施工技术, 2016, 45(1): 14−19. ZHOU Cheng, JIANG Shuangnan, LIN Xinggui. Research on UAV-based remote monitoring for risks of deep foundation excavation construction[J]. Construction Technology, 2016, 45(1): 14−19.
[2] 梅源, 胡长明, 王雪艳, 等. 西安地区湿陷性黄土地铁车站深基坑开挖引起的地表及基坑支护桩变形特性[J].中国铁道科学, 2016, 37(1): 9−16. MEI Yuan, HU Changming, WANG Xueyan, et al. Deformation characteristics of ground surface and retaining pile induced by deep foundation pit excavation of subway station in collapsible loess of Xi’an area[J]. China Railway Science, 2016, 37(1): 9−16.
[3] 梁发云, 褚峰, 宋著, 等. 紧邻地铁枢纽深基坑变形特性离心模型试验研究[J]. 岩土力学, 2012, 45(3): 657−664. LIANG Fayun, CHU Feng, SONG Zhu, et al. Centrifugal model test research on deformation behaviors of deep foundation pit adjacent to metro stations[J]. Rock and Soil Mechanics, 2012, 45(3): 657−664.
[4] STAHLHUT O, BORCHERT K M, VOIGT R E. Design and execution of a trough excavation pit in the Hamburg city center considering complex structural conditions[J]. Bautechnik, 2018, 95(1): 62−71.
[5] 王召磊, 杨志银, 张俊, 等. 桩撑锚组合支护结构的三维数值分析[J]. 岩土工程学报, 2012, 34(增刊): 230−232. WANG Zhaolei, YANG Zhiyin, ZHANG Jun, et al. Three- dimensional numerical analysis of pile-support-anchorbracing structure[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(Suppl): 230−232.
[6] 熊智彪, 欧阳中意, 王启云, 等. 深基坑桩锚支护结构锚索检测及监测分析[J]. 采矿与安全工程学报, 2009, 26(1): 123−126. XIONG Zhibiao, OUYANG Zhongyi, WANG Qiyun, et al. Test and monitoring for anchor rope of pile-anchor retaining structure in deep foundation pit[J]. Journal of Mining Safety Engineering, 2009, 26(1): 123−126.
[7] 尹静, 邓荣贵, 王金梅, 等. 锚索抗滑桩内力计算的传递矩阵法[J]. 岩土力学, 2017, 38(12): 3517−3523. YIN Jing, DENG Ronggui, WANG Jinmei, et al. Transfer matrix algorithm for calculating internal forces of anti-sliding pile with anchor cable[J]. Rock and Soil Mechanics, 2017, 38(12): 3517−3523.
[8] 冯申铎, 姜晓光, 杨志银, 等.“桩(墙)–撑–锚”联合支护技术的工程应用与变形协调探讨[J]. 岩土工程学报, 2012, 34(增刊): 456−460. FENG Shenduo, JIANG Xiaoguang, YANG Zhiyin, et al. The engineering application and deformation coordination discussion of pile−support−anchor bracing structure[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(Suppl): 456−460.
[9] 许海勇, 陈龙珠, 刘全林. 桩锚支护结构水平位移的简化算法[J]. 岩土力学, 2013, 34(8): 2321−2328. XU Haiyong, CHEN Longzhu, LIU Quanlin. A simplified algorithm of lateral displacements of pile-anchor retaining structures[J]. Rock and Soil Mechanics, 2013, 34(8): 2321−2328.
[10] 刘焕斌, 晏鄂川, 吴益平, 等. 桩锚结构预应力的变形协调确定方法[J]. 岩土力学, 2007, 28(S1): 891−894.LIU Huanbin, YAN Echuan, WU Yiping, et al. A compatible distortion method of cable in structure of pile-anchor[J]. Rock and Soil Mechanics, 2007, 28(S1): 891−894.
[11] 晏鄂川, 刘焕斌, 李相依, 等. 桩锚结构变形协调方法的改进[J]. 岩土力学, 2009, 30(5): 1446−1450.YAN Echuan, LIU Huanbin, LI Xiangyi, et al. Improvement of compatible distortion method for structure of pile-anchor[J]. Rock and Soil Mechanics, 2009, 30(5): 1446−1450.
[12] 简文星, 邓先华. 优化的变形协调条件在桩−锚结构锚索拉力计算中的应用[J]. 岩土力学, 2014, 35(8): 2171−2178.JIAN Wenxing, DENG Xianhua. Application of optimized deformation consistence condition to anchor cable tensile force calculation of pile-anchor cable structure[J]. Rock and Soil Mechanics, 2014, 35(8): 2171−2178.
[13] 杨志红, 郭忠贤. 深基坑加固锚索预应力荷载变化规律的监测分析[J]. 岩土工程学报, 2012, 34(Suppl): 145−148. YANG Zhihong, GUO Zhongxian. Monitoring analysis of pre-stressed load of anchor cables for deep excavations[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(Suppl): 145−148.
[14] 申海平, 彭文祥, 郝玉, 等. 深基坑桩锚支护结构变形的坑角效应分析[J]. 土工基础, 2016, 30(1): 73−76, 82. SHEN Haiping, PENG Wenxiang, HAO Yu, et al.Corner effect in a deep excavation supported by soldier pile and ground anchor system[J]. Soil Engineering and Foundation, 2016, 30(1): 73−76, 82.
[15] 鲍生才. 深基坑桩锚支护结构数值模拟研究[J]. 地下空间与工程学报, 2014, 10(S2): 1941−1945. BAO Shengcai. Numerical simulation study of pile anchor support structure in deep pits[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(S2): 1941−1945.
[16] 孙书伟, 朱本珍, 马惠民. 框架微型桩结构抗滑特性的模型试验研究[J]. 岩石力学与工程学报, 2010, 29(S1): 3039−3044. SUN Shuwei, ZHU Benzhen, MA Huimin. Model experimental research on anti-sliding characteristics of micropiles with cap beam[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 3039−3044.
[17] 胡敏云, 夏永承. 深基坑无锚撑护壁桩变形状态及圈梁约束分析[J]. 力学与实践, 2001, 23(1): 20−26. HU Minyun, XIA Yongcheng. The deformation and ring beam binding forces of cantilever retaining pile for excavation support[J]. Mechanics in Engineering, 2001, 23(1): 20−26.
[18] 钱同辉, 徐华, 夏文才, 等. 框架式抗滑桩受力特性对比分析[J]. 中国公路学报, 2012, 25(6): 56−59. QIAN Tonghui, XU Hua, XIA Wencai, et al. Force analysis of framed anti-slide piles[J]. China Journal of Highway and Transport, 2012, 25(6): 56−59.
[19] 铁道部第二期勘测设计院. 抗滑桩设计与计算[M]. 北京: 中国铁道出版社, 1983: 47−50. Second Survey and Design Institute of the Ministry of Railways. Design and calculation of anti-slide pile[M]. Beijing: China Railway Press, 1983: 47−50.
(编辑 陈灿华)
Theoretical model and application of anchor cable tension calculation for rib-beam-pile-anchor support structure
YIN Quan1, 2, FU Helin1, LIU Yunsi3, 4, YUE Jian3, 4, GUO Zhiguang4
(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. School of Civil Engineering, Hunan City University, Yiyang 413000, China;3. Key Laboratory of Geotechnical Engineering Stability Control and Health Monitoring of Hunan Province, Hunan University of Science & Technology, Xiangtan 411201, China;4. School of Civil Engineering, Hunan University of Science & Technology, Xiangtan 411201, China)
The rib-beam-pile-anchor support structure is different from the traditional pile anchor support structure, with the former adding the vertical rib beam to the traditional row pile. In order to solve the rib-beam pile anchor support structure, according to the equal horizontal displacement at the combined point of the rib beam, pile and anchor, the tension calculation model was built for the rib-beam-pile-anchor support structure based on the deformation coordination theory. The model was applied to calculate the anchor cable tension in a deep foundation pit engineering. The results show that with the theoretical model, the anchor cable tension is less than that of the traditional anchor support structure, and it is also closer to the actual situation of the engineering. Because of the existence of rib beam, the overall stiffness of the structure is improved, the supporting structure stress distribution is more reasonable, the prestress is smaller, the construction cost is lower, and the overall stability of the supporting structure is improved.
support of deep foundation pit; deformation coordination; ribbed beam−pile−anchor support; anchor tension force; stiffness; stability
10.11817/j.issn.1672-7207.2018.09.024
TU470
A
1672−7207(2018)09−2301−07
2018−01−10;
2018−03−16
国家自然科学基金资助项目(51538009,51578550,51704109) (Projects(51538009, 51578550, 51704109) supported by the National Natural Science Foundation of China)
尹泉,博士,讲师,从事岩土工程研究;E-mail: yinquan@csu.edu.cn
