顶燃式球式热风炉烧炉过程温度场建模

蒋朝辉，周刚，张海峰，桂卫华，阳春华，谢永芳

顶燃式球式热风炉烧炉过程温度场建模

蒋朝辉，周刚，张海峰，桂卫华，阳春华，谢永芳

(中南大学 信息科学与工程学院，湖南 长沙，410083)

针对热风炉烧炉过程中蓄热体温度难以实时在线检测的难题，结合计算流体动力学以及传热学，建立顶燃式球式热风炉烧炉过程温度场分布模型。首先，在综合分析炉内的煤气燃烧反应、烟气湍流规律和蓄热体与烟气动态热量交换过程的基础上，建立热风炉的烟气流动模型和融合蓄热球自身热传导的局部非热平衡多孔介质模型；其次，根据实际现场检测的温度、流量和压力合理设定所建模型的定解条件；最后，采用有限体积法对模型进行求解，得到热风炉的温度场分布。研究结果表明：所建立的模型能够正确、有效地模拟热风炉烧炉过程的温度场分布，模型温度计算值与实测拱顶温度的平均相对误差低于1%，与实测废气温度的平均相对误差为2.6%。

热风炉；计算流体动力学；温度场分布；多孔介质

热风炉可为高炉提供持续、稳定的高温热风，合理的热风炉操作可以提高热风炉温度、减少焦比以及节约高炉煤气用量[1−2]。蓄热体的温度是衡量热风炉烧炉状况的重要指标，根据蓄热体温度可以对热风炉烧炉过程中的煤气流量和空气流量进行实时、有效地调控。在实际工业现场，对热风炉实时检测的温度主要有拱顶温度和废气温度。由于热风炉烧炉过程中存在时滞和干扰[3−4]以及蓄热体的温度无法实时在线检测等问题，仅根据以上2个检测温度难以对热风炉进行合理、有效地控制，因此，对热风炉烧炉过程的温度场建模具有非常重要的意义。热风炉主要分为2个工作阶段：燃烧期和送风期。在燃烧期，高炉煤气和空气在燃烧室中混合后进行燃烧，产生的高温烟气自上而下流经蓄热室并对蓄热室中的蓄热体进行加热；在送风期，冷空气自下而上地流经蓄热室并带走其储存的热量，从而将高温热风被送到高炉。根据蓄热体形状和材质，蓄热室热风炉主要分为格子砖热风炉和球式热风炉共2种[5−6]。格子砖热风炉的蓄热体为形状规则、截面为等边多边形的格子砖，堆放方式整齐，各层格子砖间的气路相互连通；而球式热风炉中的蓄热球随机堆放，气路较复杂，烟气流动于蓄热球之间的缝隙中。因此，与格子砖热风炉相比，对球式热风炉烧炉过程温度场建模的难度较大。近年来，国内外利用计算流体动力学和传热学对热风炉烧炉过程的建模和数值计算发展迅速。陈义胜等[7]使用三维流动场模拟软件对建立的三维瞬态紊流模型进行了数值仿真，为热风炉的工艺结构设计提供了参考依据。CHEN 等[8]通过数值模拟分析了不同燃烧器和不同燃烧器的热风炉燃烧室内燃烧特性。戴方钦等[9]对多火孔无焰陶瓷燃烧器顶燃式热风炉内的流场温度场和可燃物浓度场进行了数值模拟。但陈义胜等[7−9]均是对设计好的热风炉燃烧性能进行验证，并没有得到整个热风炉炉内的温度场。ZHANG等[10]使用涡耗散模型对顶燃式热风炉燃烧室中的燃烧反应进行数值模拟，入口边界条件设置为高炉煤气和空气的体积流量。ZHANG等[11]根据质量、动量和能量守恒方程对顶燃式热风炉燃烧室的烧炉过程进行了稳态数值模拟，入口边界条件设置为高炉煤气和空气速度。MOON等[12]使用非预混燃烧模型对顶燃式热风炉燃烧室烧炉过程进行数值模拟，分析了高炉煤气和空气预热对烧炉过程的影响。ZHANG等[10−12]对热风炉燃烧室烧炉过程的建模和计算时均没有考虑炉内压力的变化。ZHONG等[13−16]建立了热风炉蓄热室中的传热模型，通过该模型得到了烟气和蓄热体的温度变化，但没有考虑燃烧室中高炉煤气的燃烧反应。刘红军等[17]建立了热风炉底部空间内气体流动的三维数学模型，模拟底部内空气的流动过程。KIMURA等[18]在考虑炉内压力变化的基础上建立了外燃式热风炉烧炉过程的三维模型，该模型还考虑了蓄热体与烟气间的热对流过程，但没有考虑热辐射过程。ZHANG等[19]模拟了生物质燃气的传热过程，得到了不同工况下的温度场和流场分布图，包括传热能力和总传热系数等相关参数。QI等[20−22]建立了顶燃式热风炉的三维数学模型，综合考虑了煤气燃烧、烟气湍流运动、热对流和热辐射过程，并将热风炉蓄热室当成多孔介质处理，而传统的多孔介质模型不考虑烟气与蓄热体间的换热过程。KIMURA等[18−22]所建模型的求解结果为热风炉烧炉末期的温度场分布，仅能为热风炉的工艺结构设计提供指导，对热风炉烧炉过程实时调控的意义不大。为此，本文作者在考虑热风炉炉内压力变化以及烟和蓄热体间换热的基础上，利用计算流体动力学和传热学，建立热风炉烧炉过程的温度场分布瞬态模型，包括烟气流动模型和融合蓄热球自身导热的多孔介质模型。并采用有限体积法的思想对模型进行求解，其中，蓄热体温度场是在传统多孔介质模型上融合蓄热球自身导热进行分层求解获得的。模型求解结果为各烧炉时刻热风炉的温度场，对热风炉烧炉过程的实时调控具有重要意义。

1 模型建立

热风炉从上到下主要分为拱顶、燃烧室、蓄热室和烟道4部分，根据各个区域存在介质的不同可以将这4部分分为流体域和多孔介质域，分别对不同的区域建立相应的瞬态模型。

1.1 烟气流动模型

由于拱顶、燃烧室和烟道中只存在流体，运动规律相似，因此，将这3个区域都当成流体域进行建模计算。流体运动遵守3个基本物理守恒定律，即质量守恒定律、动量守恒定律和能量守恒定律。依据这3个定律建立烟气流动过程的控制方程，具体形式如下。

质量守恒方程：

动量守恒方程：

能量守恒方程：

对于理想气体，状态方程为

式中：=8.31 J/(mol∙K)，为摩尔气体常数。热风炉炉内的流体运动方式为湍流并且是可压缩流体，为了使流体流动符合湍流运动的规律、计算准确，采用RSM模型[23]，计算方程如下：

高炉煤气与空气在热风炉拱顶中混合，并且在燃烧室中发生燃烧反应。为了处理多种化学组分间的混合和交换，建立如下组分质量守恒方程：

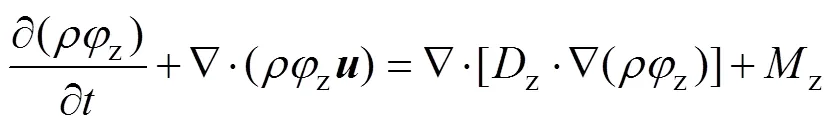
由于燃烧室中的流体在湍流状态下进行燃烧并且反应快速，故采用涡流耗散模型来模拟流体的燃烧过程。高炉煤气燃烧后的产物中有CO2和H2O等双原子结构的气体分子，故在流体燃烧和运动过程中热辐射量占热量传递的很大比例，需要将其耦合到能量守恒方程中。考虑介质的光学厚度以及计算的复杂度和准确度，采用Propagation-1辐射模型[24]。该模型假定辐射强度是各向同性的，并用正交的球谐函数表示辐射强度，将辐射能量方程转化为偏微分方程，适合于大尺度的计算，其输运方程如下：

1.2 蓄热球自身导热的多孔介质模型

在现有的热风炉工艺中，蓄热球与蓄热室的半径比小于1:100，因此，可以将蓄热室当成多孔介质进行计算。传统的多孔介质模型可以用于分析流体在蓄热室中与蓄热球的动态传热过程，只是对标准的质量、动量、能量3个守恒方程进行修正。修正方程如下。

质量守恒方程：

动量守恒方程：

能量守恒方程：

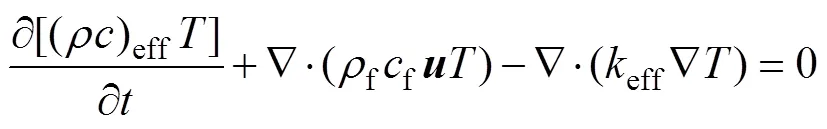
现场检测的拱顶温度为蓄热室顶部蓄热球的表面温度。而传统多孔介质模型的传热计算忽略了单个蓄热球自身的热传导以及烟气与蓄热球间的换热，实际上，计算的温度为蓄热室中纵向各位置上蓄热体和烟气的平均温度。因此，在多孔介质模型计算结果的基础上，融合蓄热室中各位置蓄热球自身的热传导。蓄热球自身的传热过程即为烟气与蓄热球间的热对流以及蓄热球从表到里的热传导，结合前面所所建立的模型，忽略蓄热球质量、组分变化，建立蓄热室中烟气与蓄热球间的非热平衡能量守恒方程：

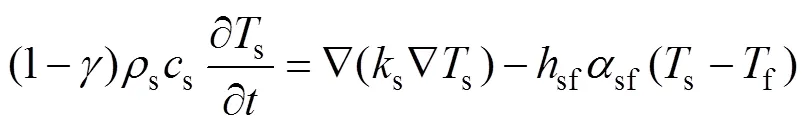
稳态条件下蓄热球的导热速率cond为

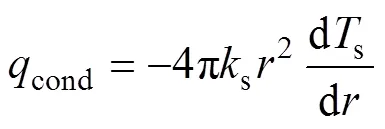
将此方程从球体表面到无穷远进行积分可得蓄热球从表到里的导热量cond为

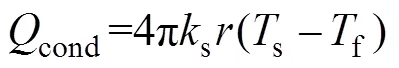
根据牛顿冷却公式，蓄热球对流换热热量conv为

2 模型计算方法

采用有限体积法对建立的烟气流动模型和多孔介质模型进行求解。先对热风炉计算域和网格进行划分，然后对模型中的方程进行离散化处理，最后确定方程的定解条件并进行迭代计算。

2.1 计算域和网格划分

计算的热风炉模型高为37.000 m，燃烧室半径为3.145 m，蓄热室截面半径为4.950 m，煤气、空气管道入口半径以及烟道口半径均为0.850 m。根据热风炉不同部位的物理化学特性，将整个热风炉化分为3个计算域，其中，拱顶和燃烧室为1个流体域，蓄热室为1个多孔介质域，烟道部分为1个流体域。采用四面体网格对煤气、空气管道、燃烧器及燃烧器管道、拱顶、燃烧室和烟道及烟道管道进行划分，采用六面体网格对蓄热室进行划分，如图1所示，网格总数为 827 200个。蓄热球的半径为0.025 m，将单个蓄热球自身传热过程的三维计算模型划分为流体域和固体域，如图2所示，网格总数为210 551个。

(a) 热风炉网格；(b) 燃烧器网格；(c) 煤气管道网格；(d) 烟气网格

(a) 蓄热球三维图；(b) 烟气网格；(c) 蓄热球网格

2.2 方程离散化

方程(1)~(13)的共同形式如下：

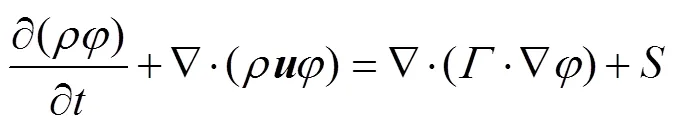
采用前向差分和中心差分的方法分别对式(18)中的4项进行三维空间和时间离散，离散结果如下：

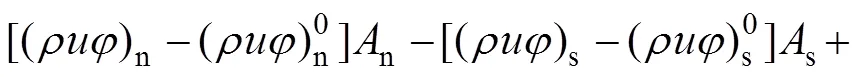
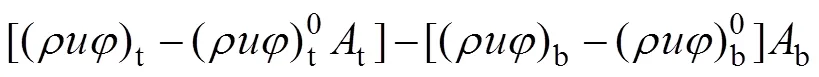
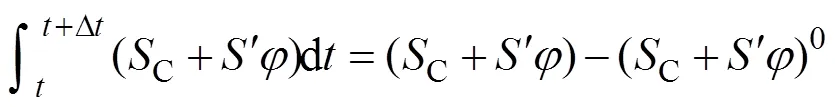
2.3 定解条件

所建模型的定解条件需结合现场热风炉实际烧炉过程中检测的温度、流量和压力确定。在热风炉烧炉过程中，考虑到气体在热风炉内是可压缩的，因此，将高炉煤气和空气入口边界条件设定为质量流量入口条件。热风炉现场实测的某烧炉周期内高炉煤气和空气体积流量如图3所示。

1—高炉煤气；2—空气。

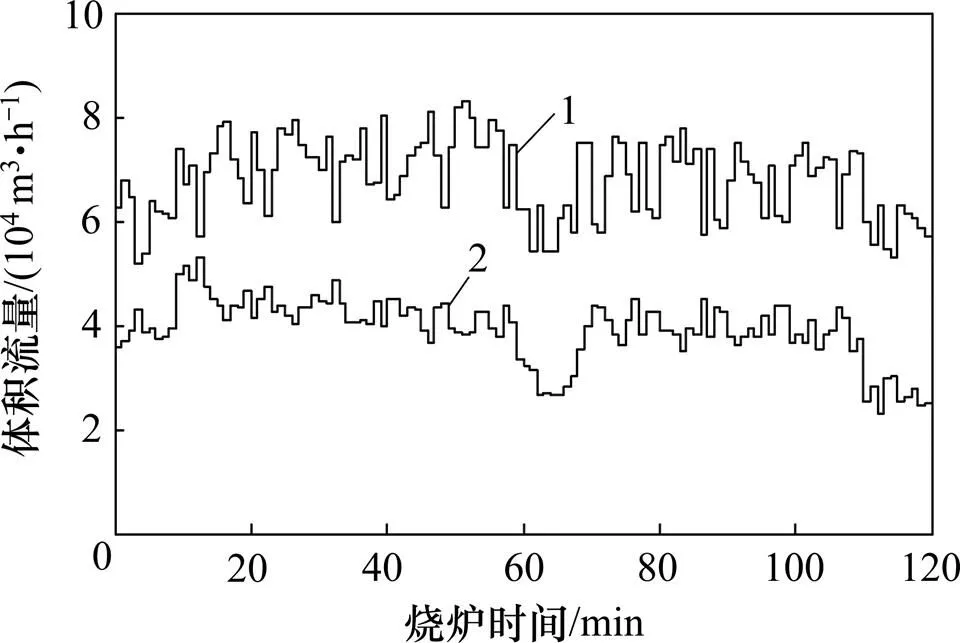
结合高炉煤气和空气的密度可将体积流量换算为质量流量，如图4所示。图4中各烧炉时刻的高炉煤气和空气质量流量即为模型计算的入口边界条件。实测的高炉煤气温度为150℃，空气温度为200℃，将其设为高炉煤气和空气的入口温度。高炉煤气成分及其体积分数如下：CO为0.22，H2为0.02，CO2为0.20，N2为0.56。

1—高炉煤气；2—空气。

将烟道的出口边界条件设置为压力出口，相对静压初始值设置为0 Pa，热风炉与外界接触的壁面均假设为绝缘隔热。蓄热室中蓄热球的成分设置为耐火材料，其物性参数如下：密度为2.645 t/m3，比热容为960 J/(kg∙K)，导热系数为1.0 W/(m2∙K)。

蓄热球自身导热模型求解需要的定解条件根据多孔介质模型求解结果设定。上底面为烟气质量入口，对比单个蓄热球三维模型的截面面积与热风炉蓄热室的截面面积并结合煤气和空气质量流量可得烟气入口质量流量如图5所示。

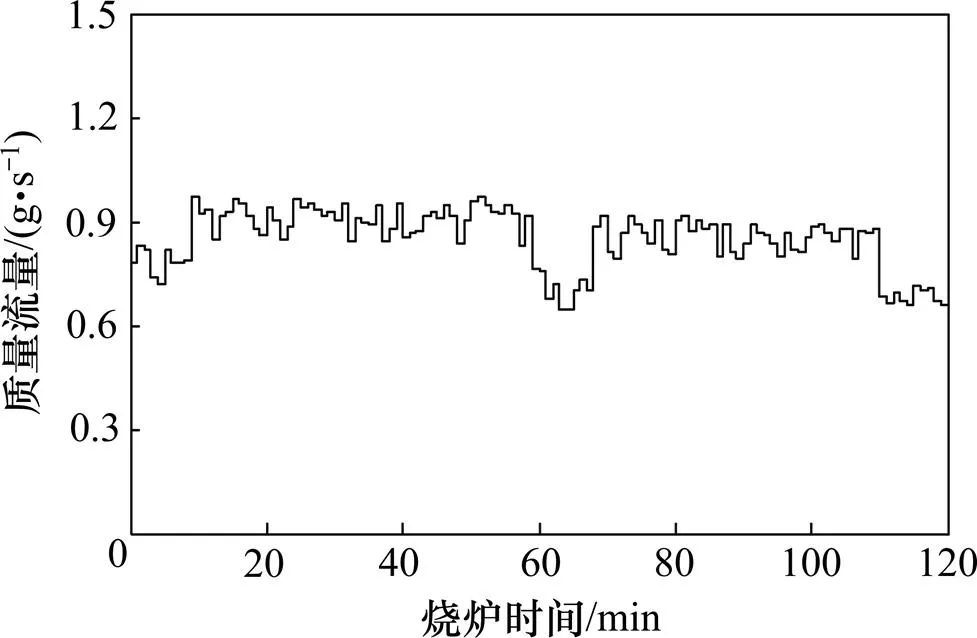
图5 烟气质量流量变化图

烟气温度为对应蓄热室各位置求解的烟气温度，烟气的成分体积分数如下：CO2为0.25，H2O为0.06，N2为0.65，O2为0.04。下底面为压力出口，初始压力为0 Pa，4个侧面为隔热壁面。

根据给定的定解条件对离散后的方程进行迭代求解，其计算流程图见图6。

3 模型求解结果与讨论

基于ANSYS仿真软件，采用有限体积法对建立的温度场分布模型进行求解，求解时间为120 min，时间步长为0.1 s。图7所示为烧炉过程在不同时间顶部蓄热球的温度变化。从图7可以看出：在烧炉前15 min内，蓄热球的温度变化明显，并且蓄热球从表到里的温度呈现出梯度分布。这是由于烟气与蓄热球表面进行快速热交换以及蓄热球自身的热传导过程使蓄热球表面温度比里面温度高；而在烧炉30 min后，烟气与蓄热球的热交换减弱，蓄热球的蓄热量已经趋于饱和，温度基本上保持不变。

图6 热风炉温度场计算流程

图8所示为热风炉在烧炉过程在不同时间周期的温度分布。从图8可以看出：在整个热风炉中，流体温度呈现分层分布的规律；预燃室的温度比较低，为200℃左右，与设置的高炉煤气和空气入口温度一致；燃烧室的流体温度最高，高温区域比较集中，温度分布比较明显，温度分布不对称是热风炉结构的不对称以及湍流运动所致。而蓄热室的温度呈对称分布，这是因为烟气与蓄热球对流换热比较均匀；蓄热室的流体温度呈现明显的分层分布，温度梯度较大，从 1 370℃降到200℃；烟道温度最低，为200~350℃；在烧炉10 min后，燃烧室的烟气温度达1 370℃，且逐渐趋于稳定。这说明燃烧室中煤气燃烧过程十分迅速。由于给定的煤气成分和煤气热值为常值，煤气燃烧产生的烟气温度会趋于1个稳定值。在烧炉初期即烧炉40 min内，蓄热室顶部的温度逐渐上升并趋于稳定，而烟道的温度基本上不发生变化。这是因为在烧炉初期，煤气燃烧产生的高温烟气主要给蓄热室顶部的蓄热球进行加热，随着烟气与蓄热球间温差不断缩小，蓄热球的蓄热量已经趋于饱和，温度不会继续增大。在烧炉中后期即在烧炉40 min后，烟气的热量逐渐往蓄热室的中、下层传递。因此，随着烧炉的进行，温度分布曲线下移，烟道中废气的温度开始上升，从200 ℃不断增加到350℃。废气温度上升说明热风炉内积蓄的热量增大，当上升到其上限温度时，热风炉从烧炉转为送风阶段，这是因为废气温度不能超过热风炉炉箅子的安全温度。热风炉现有可检测的2个重要指标为拱顶温度和废气温度，通过比较模型计算和检测的拱顶温度以及废气温度，可知计算结果的准 确性。

时间/min：(a) 0；(b) 2；(c) 8；(d) 15；(e) 30；(f) 120

时间/min：(a) 10；(b) 40；(c) 60；(d) 80；(e) 100；(f) 120

模型计算的拱顶温度和废气温度与温度检测值的对比结果见图9，其中，图9(a)所示为实际检测的蓄热室顶部温度、传统多孔介质模型计算的拱顶温度、融合蓄热球自身导热计算的拱顶温度和烟气流动模型计算的蓄热室顶部烟气温度变化趋势。从图9(a)可以看出：模型计算的蓄热室顶部烟气温度在开始燃烧后就达到高炉煤气的理论燃烧温度，即1 370 ℃左右；模型计算的拱顶温度随着烧炉过程的进行不断增大，从1 200℃增大到1 350℃，其温度上升速率随着烧炉时间的推移不断减小，这是因为蓄热球的蓄热量逐渐趋于饱和状态；拱顶温度计算值在整个烧炉过程中比计算的烟气温度小，这是因为烟气是蓄热球的热量来源；直接使用多孔介质模型计算的拱顶温度与温度检测值相差较大，平均相对误差为5.6%；而融合蓄热球自身导热后计算的拱顶温度与实际检测的拱顶温度十分接近，最大相对误差为3.6%，平均相对误差低于1.0%，因此，融合蓄热球自身导热后计算的各层蓄热球温度更加准确。图9(b)所示为烟道中废气温度检测值、废气温度计算值、传统多孔介质模型计算的蓄热室底部蓄热球温度和融合蓄热球自身导热计算的蓄热室底部蓄热球温度变化趋势。从图9(b)可见：废气温度在烧炉初期变化不大，在烧炉中后期不断增大并且上升速率也逐步变大；模型计算的废气温度与温度检测值相比相差较小，平均相对误差为2.6%，最大相对误差低于4.0%；传统多孔介质模型计算的蓄热球温度与废气温度相等，这是由于其没考虑烟气与蓄热体间的热交换；而融合蓄热球导热计算的蓄热球温度比废气温度小，更符合实际情况。因此，本文中建立的模型能准确地反映热风炉在实际烧炉过程中的温度 变化。

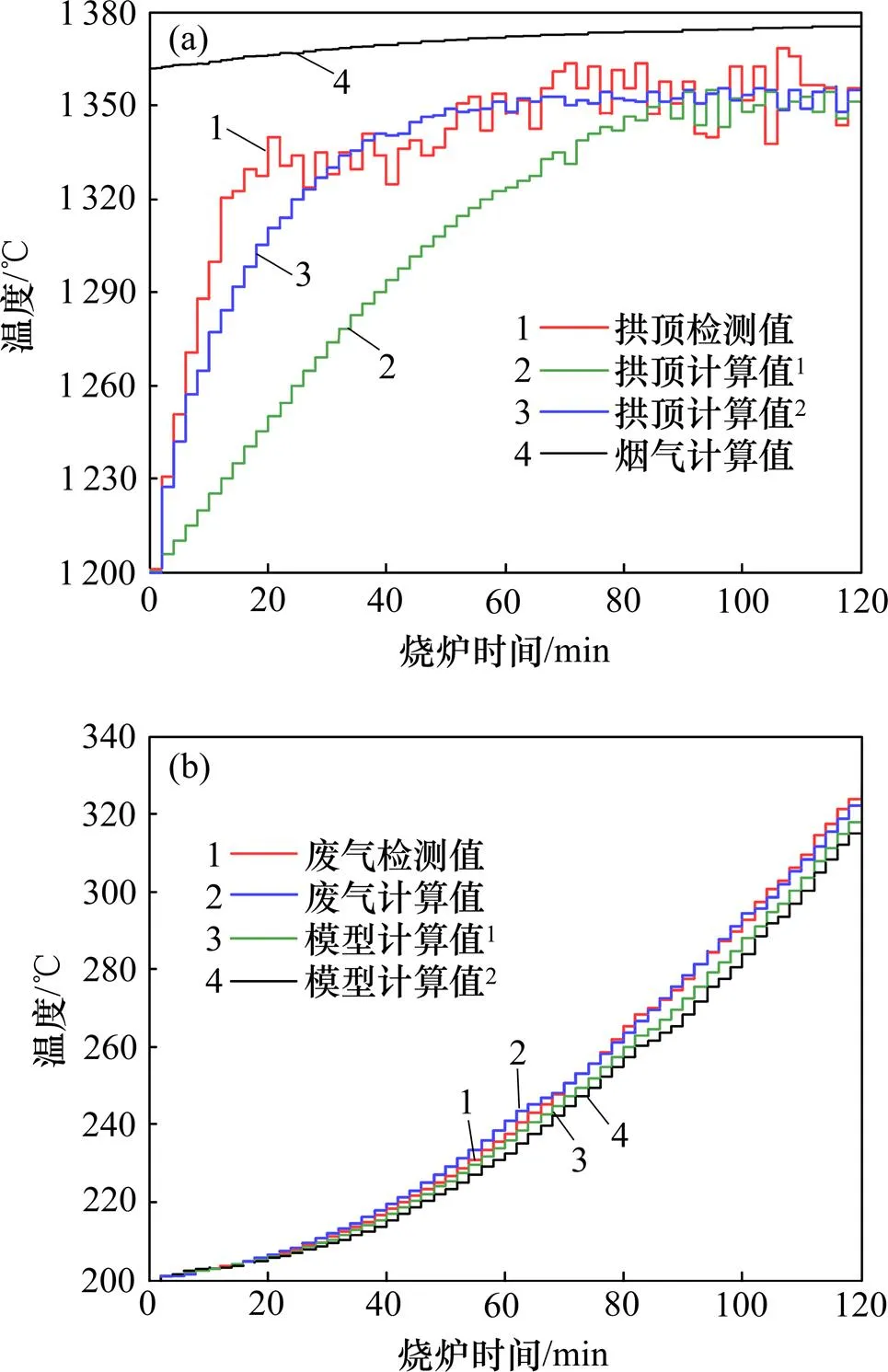
(a) 拱顶温度；(b) 烟道温度

4 结论

1) 在考虑炉内压力变化和蓄热球自身导热的情况下，建立了顶燃式球式热风炉的三维温度场分布瞬态模型，并对此模型进行求解。该模型能够有效地模拟出热风炉在烧炉过程中蓄热球温度场变化的过程，对热风炉烧炉过程进行实时、有效地控制具有重要的指导作用。

2) 与传统的多孔介质模型相比，融合蓄热球自身导热后计算的顶层蓄热球温度更接近于实际检测值。因此，在多孔介质模型基础上融合蓄热球自身导热对各层蓄热球的温度场分别求解，可以提高蓄热球温度场计算结果的准确性。

[1] 项中庸, 王筱留. 高炉设计−炼铁工艺设计理论与实践[M]. 北京: 冶金工业出版社, 2007: 463−464. XIANG Zhongyong, WANG Xiaoliu. Design theory and practice of blast furnace design and iron making process[M]. Beijing: Metallurgical Industry Press, 2007: 463−464.

[2] 黄飞, 刘峰, 孙健. 钢铁企业煤气蒸汽余热整体利用方案应用[J]. 冶金能源, 2014, 3(5): 9−12. HUANG Fei, LIU Feng, SUN Jian. Application on overall utilization about steam gas waste heat of iron and steel enterprises[J]. Energy for Metallurgical Industry, 2014, 3(5): 9−12.

[3] 樊波, 齐渊洪, 严定鎏, 等. 热风炉燃烧控制技术的研究[J]. 钢铁, 2005, 40(4): 17−20. FAN Bo, QI Yuanhong, YAN Dingliu, et al. Study on combustion control technology for hot blast stove[J]. Iron and Steel, 2005, 40(4): 17−20.

[4] 马竹梧. 高炉热风炉自动换炉的研究和应用实践[J]. 冶金自动化, 2007, 31(2): 29−32. MA Zhuwu. Research on automatic changeover of hot blast stoves for blast furnace and its application in practice[J]. Metallurgical Industry Automation, 2007, 31(2): 29−32.

[5] CHENG Lanbo. Calculation of blast furnace iron making process[M]. Beijing: Metallurgical Industry Press, 1991: 94−95.

[6] 陈林森, 黄东升. 新型顶燃球式热风炉的设计和实践[J]. 山西冶金, 2015, 38(2): 59−60. CHEN Linsen, HUANG Dongsheng. The design and practice of new top combustion hot-blast stove[J]. Shanxi Metallurgy, 2015, 38(2): 59−60.

[7] 陈义胜, 张捷宇, 那树人, 等. 热风炉蓄热室内气流分布的计算机模拟研究[J]. 钢铁, 2000, 35(8): 11−14. CHEN Yisheng, ZHANG Jieyu, NA Shuren, et al. Study on computer simulation of flow distribution in hot blast stove checker[J]. Iron and Steel, 2000, 35(8): 11−14.

[8] CHEN Shanshan, KONG Dewen, PEI Yi, et al. Numerical simulation on structure optimization for hot-blast stove burner[C]// China Energy Scientist Forum. Xuzhou, China, 2010: 466−470.

[9] 戴方钦, 张喜来, 李少华, 等. 多火孔无焰陶瓷燃烧器顶燃式热风炉的数值模拟[J]. 钢铁研究学报, 2010, 22(6): 1−6. DAI Fangqin, ZHANG Xilai, LI Shaohua, et al. Numerical simulation of hot stove with multi- channel annular flameless ceramic burner[J]. Journal of Iron and Steel Research, 2010, 22(6): 1−6.

[10] ZHANG Bingzhe, ZHANG Xinxin, YU Fan, et al. Numerical simulations of gas combustion and flow in Kalugin hot blast stove[J]. Industrial Furnace, 2005, 27(6): 1−8.

[11] ZHANG Fuming, MAO Qingwu, MEI Conghua, et al. Dome combustion hot blast stove for huge blast furnace[J]. International Journal of Iron and Steel, 2012, 19 (9): 1−7.

[12] MOON J W, KIM S J, SASAKI Y. Effect of preheated top gas and air on blast furnace top gas combustion[J]. Journal of Iron and Steel Research, 2012, 54(1): 63−71.

[13] ZHONG Liangcai, LIU Quanxing, WANG Wenzhong. Computer simulation of heat transfer in regenerative chambers of self-preheating hot blast stoves[J]. ISIJ International, 2004, 44(5): 795−800.

[14] 杜长坤, 何鸿福, 陈克祥, 等. 热风炉蓄热室传热过程的数值模拟与应用[J]. 冶金能源, 2012, 31(4): 30−34. DU Changkun, HE Hongfu, CHEN Kexiang, et al. Numerical simulation and application on heat transfer process of regenerator[J]. Energy for Metallurgical Industry, 2012, 31(4): 30−34.

[15] 文午琪, 黄素逸, 靳士奇, 等. 热风炉蓄热室流动和传热过程数值模拟[J]. 工业加热, 2012, 41(3): 23−27. WEN Wuqi, HUANG Suyi, JIN Shiqi, et al. Numerical simulation of flow and heat transfer process in hot blast stoves regenerator[J]. Industrial Heating, 2012, 41(3): 23−27.

[16] 杨宽, 树森, 陈川. 豫兴Ⅱ型顶燃式热风炉燃烧室燃烧过程数值模拟[J]. 工业炉, 2015, 37(5): 1−5.YANG Kuan, CHENG Shusen, CHEN Chuan. Numerical simulation of combustion process in combustion chamber of Yuxing Ⅱtype top combustion hot blast stove[J]. Industrial Furnace, 2015, 37(5): 1−5.

[17] 刘红军, 宇永香, 齐凤升. 顶燃蓄热式热风炉底部空间空气流动特性模拟研究[J]. 中国冶金, 2013, 23(9): 13−16. LIU Hongjun, YU Yongxiang, QI Fengsheng. Numerical study on flow character in bottom zone of top combustion regenerative hot air stove[J]. China Metallurgy, 2013, 23(9): 13−16.

[18] KIMURA Y, TAKATANI K, SUN O. Three-dimensional mathematical modeling and designing of hot stove[J]. ISIJ International, 2010, 50(7): 1040−1047.

[19] ZHANG Jiangyong, SUN Huanwu, LI Ji, et al. Structural optimization and numerical analysis study in heat exchanger of biomass hot blast stove[J]. Journal of Agricultural Mechanization Research, 2013, 9(3): 1−7.

[20] QI Fengsheng, LIU Zhongqiu, YAO Chaoyi, et al. Numerical study and structural optimization of a top combustion hot blast stove[J]. Advances in Mechanical Engineering, 2015, 2(7): 709675−709675.

[21] QIAN Shichong, ZHANG Fumin, LI Xin, et al. Technical analysis on hot blast stove of large capacity blast furnace[J]. Iron & Steel, 2011, 46(10): 1−6.

[22] 何增晓, 邢桂菊. 卡鲁金顶燃式热风炉燃烧器的燃烧过程模拟研究[J]. 天津冶金, 2013, 16(z1): 51−53. HE Zengxiao, XING Guiju. Simulation study on combustion process of Kalugin top combustion hot blast stove burner[J]. Tianjin Metallurgy, 2013, 16(z1): 51−53.

[23] ZHOU Bonan, YANG Mo, LI Zheng, et al. Numerical simulation s of forced convection across a single tube to evaluate applicability of the DNS, LES and RSM methods[J]. Applied Thermal Engineering, 2017, 123(8): 123−130.

[24] BÉG O A, ALI N, ZAMAN A, et al. Computational modeling of heat transfer in an annular porous medium solar energy absorber with the P1-radiative differential approximation[J]. Journal of the Taiwan Institute of Chemical Engineers, 2016, 66(9): 258−268.

(编辑 陈灿华)

Temperature distribution model for combustion process of hot blast stove of dome combustion ball type

JIANG Zhaohui, ZHOU Gang, ZHANG Haifeng, GUI Weihua, YANG Chunhua, XIE Yongfang

(School of Information Science and Engineering, Central South University, Changsha 410083, China)

Considering that the heat storage temperature is difficult to detect online in the combustion process of hot blast stove, temperature distribution model for combustion process of dome combustion ball type hot blast stove was developed by computational fluid dynamics(CFD) and heat transfer theory. Firstly, considering gas combustion, flue gas flow and heat exchange, the flue gas flow model and the local thermal non-equilibrium porous medium model with heat conduction of regenerative balls were built. Then, the reasonable boundary conditions were set by the measured temperature, flow rate and pressure. Finally, the temperature distrubution of hot blast stove was obtained by finite volume method. The results show that the model can correctly simulate the temperature distribution of hot blast stove, the average relative error is less than 1% compared with the measured dome temperature and the average relative error is about 2.6% compared with the measured exhaust gas temperature.

hot blast stove; computational fluid dynamics(CFD); temperature distribution; porous medium

10.11817/j.issn.1672-7207.2018.09.014

TP29

A

1672−7207(2018)09−2216−09

2017−10−25；

2017−12−13

国家自然科学基金重大资助项目(61290325)；国家自然科学基金创新研究群体科学基金资助项目(61621062)；研究生自主探索创新项目(2017zzts495) (Project(61290325) supported by the Major Program of the National Natural Science Foundation of China; Project(61621062) supported by the Foundation for Innovative Research Groups of the National Natural Science Foundation of China; Project(2017zzts495) supported by the Graduate Students' Independent Exploration of Innovative Projects)

蒋朝辉，博士，副教授，从事复杂工业过程建模与优化控制研究；E-mail: jzh0903@csu.edu.cn