基于鉴别混合结构保持投影的人脸识别算法
2018-10-13王成国胡西川
王成国,胡西川
(上海海事大学信息工程学院,上海 201306)
0 引言
人脸识别近些年来一直是研究的热门领域,由于人脸图像处在一个高维度的空间,避免“维数灾难”,发现数据真实存在的子空间,维度的简约显得非常重要。目前有大量的降维算法已经被提出,例如主成分分析(PCA)[3]、线性判别分析(LDA)[4]等。这些方法属于线性降维方法。由于这些线性方法无法发现复杂非线性数据的固有结构,近些年来,流行学习方法作为可以处理非线性数据的方法被大量的研究。其中具有代表性的方法有局部线性嵌入(LLE)[5]、拉普拉斯特征映射(LE)[6]算法,这些算法可以将数据的结构从原始高维空间投影到低维空间后得到最大的保持,然而这些方法无法给定一个显示的映射,对于增量数据无法处理。同时实际生产数据中数据没有严格的流形结构,使算法收到局限性。作为LLE的线性化方法邻域保持嵌入(NPE)[7]算法和LE算法的线性化方法局部保持投影(LPP)算法克服了这些缺点并得到广发的应用。但这两种方法也有缺点,他们对邻域的大小和边权值参仍然无法确定。最近Qiao等人提出了根据稀疏表示理论提出了稀疏保持嵌(SPP)[8]算法,该算法将数据投影到低维空间的同时保持数据之间的稀疏表示性,此算法可以自动的选择用哪些其他数据来线性表示待表示数据,一定程度上克服了NPE和LPP的需要确定邻域参数和边权值的缺点。
邻域表示和稀疏表示各有其优缺点,对于低维数据来说,邻域表示比稀疏表示更加重要,而对于高维数据来说稀疏表示更加有用[1]。可以结合两者的优点来表示数据,使其更加准确地反映数据的特征。Zhang等人通过融合NPE算法和SPP算法中近邻表示和稀疏表示提出了一种混合表示结构,充分地利用了数据的近邻结构和稀疏结构,在降维投影方面表现出优势。本文将数据的鉴别信息加入到混合结构保持投影算法中,再结合改进的最大余量准则,将充分利用数据的类别信息,从而在获得的投影空间中更容易将数据进行分类。
1 相关工作
(1)NPE算法
NPE可以认为是LEE算法的线性化改进,它是一种线性化降维方法。NPE的目标是保持投影空间中数据的局部邻域结构,NPE使用局部最小二乘法来计算亲和度矩阵。算法步骤如下:
首先构造一个邻近图,对应邻近图设置重构权重系数矩N,Nij满足:
如果xj不是xi的近邻点,则Nij=0,否则Nij≠0。
对于非零的Nij的大小可以通过最小化如下损失函数来计算:
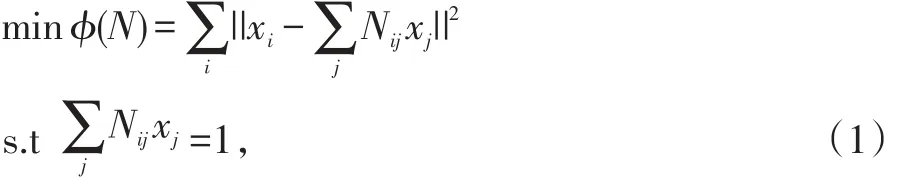
上式进一步可写为:

其中:N=[n1,n2,...,nn]。
最优投影w是通过最小化如下损失函数获得的:
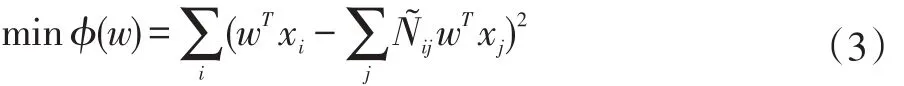
其中 N˜ij是(1)式的最优解。进一步化简可得:

求解上式广义特征向量可得投影矩阵W。
(2)SPP算法
SPP同NPE一样也是一种线性降维方法,SPP在稀疏表示[9]原理的基础上,通过把原始空间中的数据投影到投影空间,同时保持数据的稀疏结构关系不变,从而达到降维的作用。
SPP的计算步骤如下:
首先,对于每一个xi的稀疏表示向量si可以通过求解如下l1正则项最小问题来求解:

或者考虑噪音的情况下变化为如下:
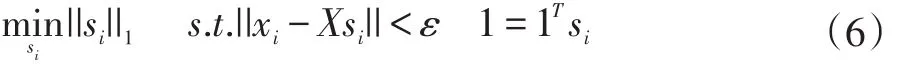
然后,稀疏表示系数矩阵i表示为:

最后,我们可以通过优化如下问题来获得最优的投影向量w:

其中:Sβ=S+ST-STS。
求解上式获得投影矩阵W。
(3)SNPP算法
该算法根据NPE算法和SPP算法的相似性,通过深度整合NPE和SPP的结构到一个混合结构中,提出了一种新线性降维方法,此方法既保持数据的稀疏性,又保持了数据的近邻关系。在高维空间或者低维空间都有较好的性能表现。
本算法的目标函数是:

其中 zi=αni+βsi,ni是(2)式邻域表示系数向量,si是(7)式稀疏表示系数向量。
α和 β是反映s和w重要性的两个参数。α β取值范围是[-1,1]。
求解方法上式可得最优解W。
(4)MMMC算法
MMMC由Song等人提出,他们将最大间隔准则(MMC)算法中类内散度和类间散度的差改为商的形式,这样就避免了在传统方法中发生的小样本问题,从而更有利于分类。MMMC函数定义如下:

进一步可获得如下形式:
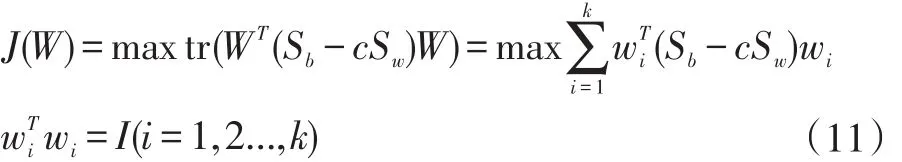
将上式可转化为求解最大特征值问题,从而求得最优投影W。
2 基于鉴别混合结构保持投影的线性降维算法(DSNPP)
本文针对SNPP算法作为一种无监督降维方法,没有充分利用类别鉴别信息的缺点,通过将数据的近邻性和稀疏性加上鉴别信息,以及结合最大余量原则(MMMC)充分数据的鉴别信息,提出了鉴别混合结构保持投影的线性降维算法(DSNPP)的有监督的降维方法,增强的降维后数据的分类效果。
算法步骤如下:
第一步,用鉴别邻域保持嵌入来替代邻域保持嵌入算法来获得邻域保持系数矩阵N。首先构造邻域图时,加入类别鉴别信息。先选择与xi属于同一类别的k个近邻点,再选择不同类的k个近邻点。设置权值矩阵时,与xi不相近邻的点的边权重设置为0;在与xi相近邻的点的边权重分两种情况,若与xi属于同一类别则权重提高为(1+β)nij(β>0),否则,如不是同一类则保持nij不变,获得邻域表示系数矩阵N=[n1,n2,…,nn],来替代(2)式的邻域表示矩阵。
第二步,获得将鉴别信息加入到稀疏表示后的稀疏表示系数矩阵S。将(5)、(6)式加入判别信息修改为如下:

或者是:
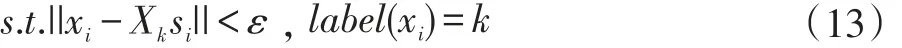
由此得到的稀疏表示矩阵S=[s1,s2,...,sn],来替代(7)式获得的稀疏表示矩阵。
第三步,获得复合结构的投影矩阵Z,其中:

第四步,构造改进的SNPP目标函数:
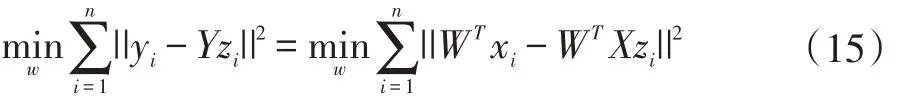
对上式求解广义特征值问题可得到:

增加约束:wTXXTw=1,避免解的退化。
第五步,我们希望投影矩阵满足最大余量准则,如下有:
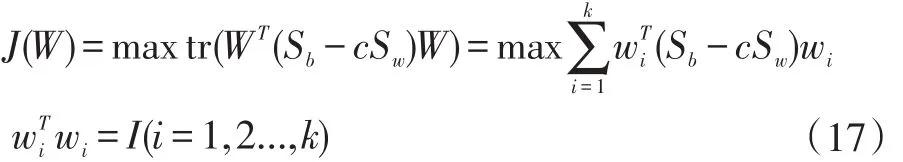
最后:构造最终的目标函数:
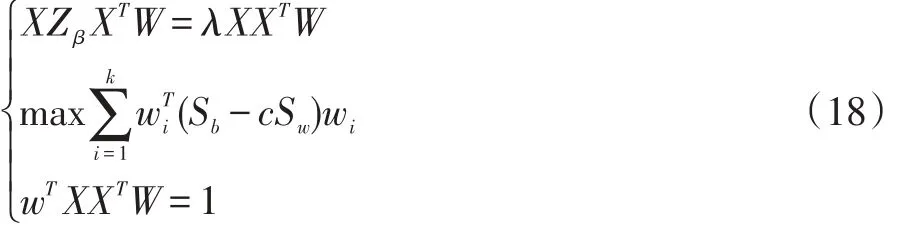
以上优化问题可以转化为如下:
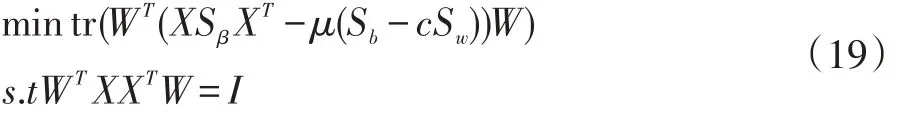
利用拉格朗日乘子法对上式求解得:

从而可得到:
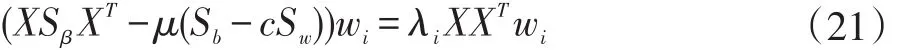
求解上式广义特征值特征向量从而可以求得最优解W。
3 实验
为了验证DSNPP算法的有效性,分别在AR、PIE人脸数据库上将 PCA、NPE、SPP、SNPP、DSNPP 算法进行实验对比。本文随机选择图像,并重复实验10次,平均值作为最后的输出结果。经实验可知,参数μ和c取值对实验结果无影响,其中固定参数 μ=1,c=1。在降维投影空间我们使用KNN最近邻算法最为最终分类算法,并取k=1。α和β的取值按照网格搜索,从-1到1,每步0.05增加。SNPP中邻域大k的取值与NPE中k的取值相同,DSNPP中α和 β取值与SNPP中相同。ε=0.05。实验前我们首先用PCA将原始数据降维为200维。
(1)AR人脸数据库的实验
该数据库由126个人的超过4000张人脸图像组成。对于每个人,有26张照片,其中13张照片没有遮挡,另外13张照片有遮挡。实验中使用AR人脸数据库的一个子集,包含与100人(50名男性和50名女性)相对应的1400张面部图像,其中每个人具有14个不同的具有照明改变和表情的图像。这些图像面的原始分辨率为165×120。这里,为了便于计算,我们将它们调整为32×32,并将灰度值重新调整为[0 1]。部分人脸图像如图1所示。

图1 AR人脸数据库的部分人脸图像
参数选择:NPE中k=23,α=0.95,β=0.1。实验中每个人选取p张照片作为训练集,剩余照片作为测试集。图2显示了p=3,5,8,10时,识别准确率随时间的变化。
PCA、NPE、SPP、SNPP、DSNPP 算法在 AR 人脸数据库上的最高设别率如表1所示
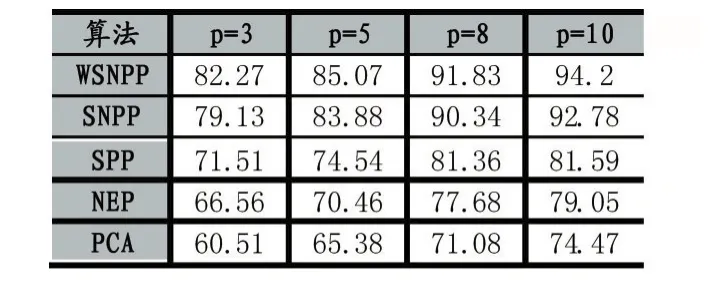
表1 算法在AR人脸库上的最高识别率
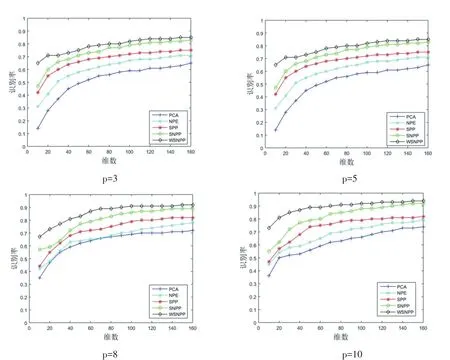
图2 不同维度下照片识别准确率(AR数据库)
(2)PIE人脸数据库上的实验
PIE人脸数据库含有68个人,每个人13种姿势,43种光照条件,4种表情,共41368张图片。本文选择在所有光照条件和表情条件下的5个近似正向的姿态,每个人170张,总共11560张图片。图3显示了PIE人脸库中部分人脸图像。表2显示了算法在PIE数据库上的最高识别率。
图3 PIE人脸数据库的部分人脸图像
参数选择:NPE中k=17,α=-0.15,β=0.6。实验中每个人选取p张照片作为训练集,剩余照片作为测试集。表2列出了p=30,35,40,45时,识别准确率随时间的变化。
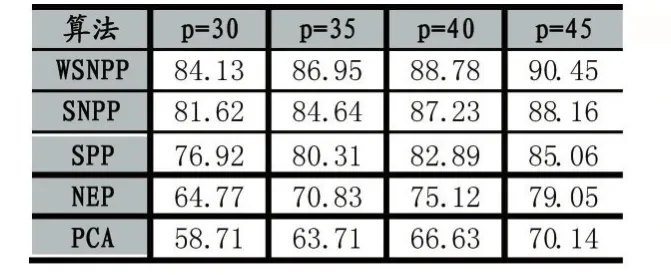
表2 算法在PIE人脸库上的最高识别率
4 结语
本文在分析SNPP算法和MMMC算法的基础上,利用判别信息,对SNPP算法进行了改进,提出了判别SNPP算法,给出了详细的推导过程和具体步骤,并利用最近邻分类器实现了分类。最后在两个人脸数据库上进行大量的仿真实验,证明了该算法不论在低维还是高维数据中都有较高的识别准确率,是一种鲁棒性比较好的算法。
