Minitab软件在大豆水分生产函数模型建立与评价中的应用

陶延怀，郑文生

(1.黑龙江省水利科学研究院，黑龙江 哈尔滨 150080;2.黑龙江省寒区农业节水工程重点实验室，黑龙江 哈尔滨 150080)

作物水分生产函数是指农业种植水平基本一致的情况下作物产量与所消耗的水量之间的函数关系。当前，国内外主要是利用Excel、SAS和MATLAB等软件对水分生产函数模型进行分析求解，本文尝试使用Minitab软件对大豆水分生产函数模型进行分析评价[1-4]。Minitab统计分析软件包最初是由美国宾夕法尼亚州立大学发展起来的产品，已有30多年的历史。其特点是具有操作简便、软件兼容性能好、功能多、精度高(双精度计算)、对硬件的要求低、有最新现代化图表引擎、强大的宏等功能[5]。

1 材料与方法

1.1 试验设计

2008年，本试验在黑龙江省西部松嫩平原齐齐哈尔市甘南县兴隆乡开展。该地区土壤类型为黑钙土，为了控制土壤水分，试验选用移动式遮雨棚。根据试验目的选用PVC塑料桶57个，桶高33 cm，直径29 cm。取当地耕地表层0～20 cm的土壤，过筛，然后装入塑料桶内。每桶底肥一致，一次施入。选择大豆苗期、分枝、开花、结荚、鼓粒期5个阶段，进行水分胁迫调控，土壤相对含水量水平(占田间持水量的百分比)：70%～80%(轻度受旱，下限为70%)、60%～70%(中度受旱，下限为60%)，试验设置如表1，3次重复。土壤水分测定采用称重法，全生育期控制土壤水分含量。大豆品种选择当地主栽品种垦农18，5月20日播种，出苗后，每桶定苗4株。全生育期土壤水分含量控制采用电子天平称重，每日17:00称量每桶的重量，称重后，补水至控水标准。9月25日收获考种测产。

1.2 水分生产函数模型选取

本研究选用Jensen(1968)模型、Minhas(1974)模型、Blank(1975)模型、Stewart(1976)模型和Singh(1987)模型5种模型，分析黑龙江西部半干旱区大豆水分生产函数。

表1 各生育阶段不同水分处理 %

注：处理19为适宜肥量下的丰水处理，该处理的作物需水量设定为作物蒸发蒸腾量。

1.3 模型检验方法

本文选择平均误差(AE)、均方根误差(RMSE)、变异系数(Cv)、残差聚集系数(CRM)和模型性能指数(EF)[6-7]等统计参数，评价水分生产函数模型模拟值与实测值之间的模拟结果。

2 结果与讨论

根据2008年甘南大豆盆栽试验的实测资料进行分析计算，各生育期及全生育期耗水量与大豆产量见表2。

表2 耗水量及产量

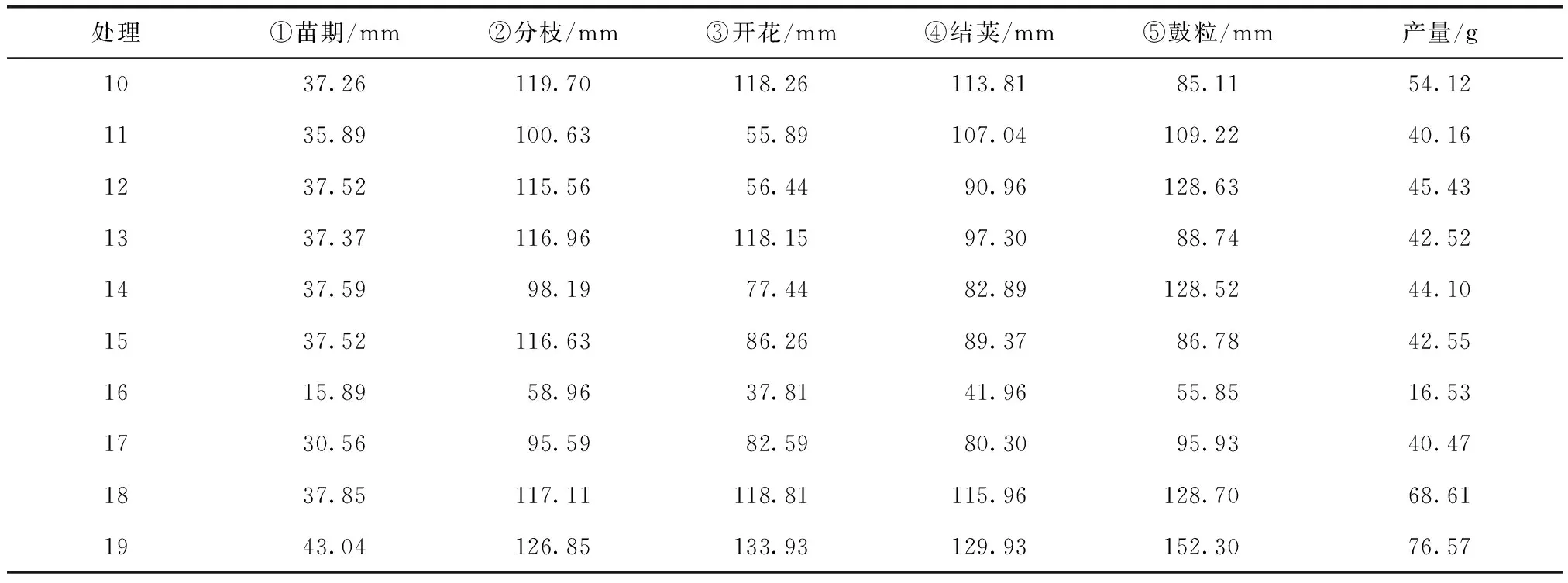
续表2

2.1 模型参数的确定

根据实测的大豆耗水量和产量数据(表2)，应用Minitab 15统计软件分析求解，即可得到5种水分生产函数模型中的敏感指数及相关参数。计算结果见表3。

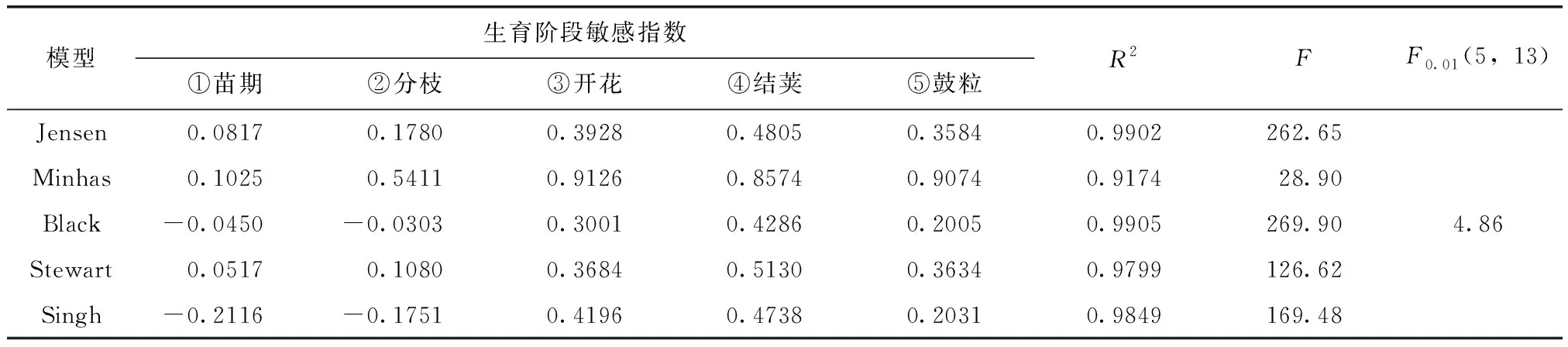
表3 水分生产函数敏感指数及回归方程的显著性检验

注：R为复相关系数

(1)Blank模型和Singh模型的敏感参数变化规律与大豆的水分生理特性以及灌溉的实际经验相矛盾，而且还有负值出现，不宜采用。

(2)在Jensen模型、Minhas模型和Stewart模型中，F检验结果表明，各模型方程拟合达到极显著水平，复相关系数R值表明，Jensen和Stewart模型拟合效果最好，Minhas模型拟合效果次之。

(3)对于Jensen模型，大豆水分亏缺敏感性为结荚期最敏感，开花期次之，苗期最不敏感，在该模型中缺水后各阶段敏感顺序与大豆的水分生理特性以及灌溉的实际经验是一致的，而且模型的相关系数在0.99以上，模型方程拟合效果最好，因此大豆是比较适合该模型的。其水分生产函数模型为：

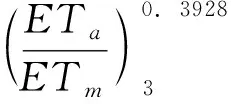
(1)

式中：Ya为各处理条件下的实际产量，kg/hm2；Ym为正常灌溉下的产量，kg/hm2；ETa为各处理条件下的实际蒸发量，mm；ETm为正常处理下的蒸发量，mm；1、2、3、4、5为模型的阶段数。

2.2 模型精度评价

为了进一步验证Jensen、Minhas和Stewart模型的模拟效果，应用Jensen、Minhas和Stewart模型计算大豆模拟相对产量，然后计算各模型模拟效果，结果见表4。由表4知各模型对于大豆相对产量的模拟效果排序为Jensen模型最好，Stewart模型次之，Minhas模型模拟效果最差。Jensen模型对于大豆相对产量的模拟效果最好，平均误差(AE)、变异系数(Cv)和均方根误差(RMSE)分别为0.0067、6.34%和0.0380，均小于其他两种模型；而对于反映模型整体模拟能力的模拟性能指数EF，其值为0.94，大于其他模型。对残差聚集系数CRM进行对比分析表明，Jensen模型对于大豆相对产量模拟值偏高，与其他模型相比最接近于零。

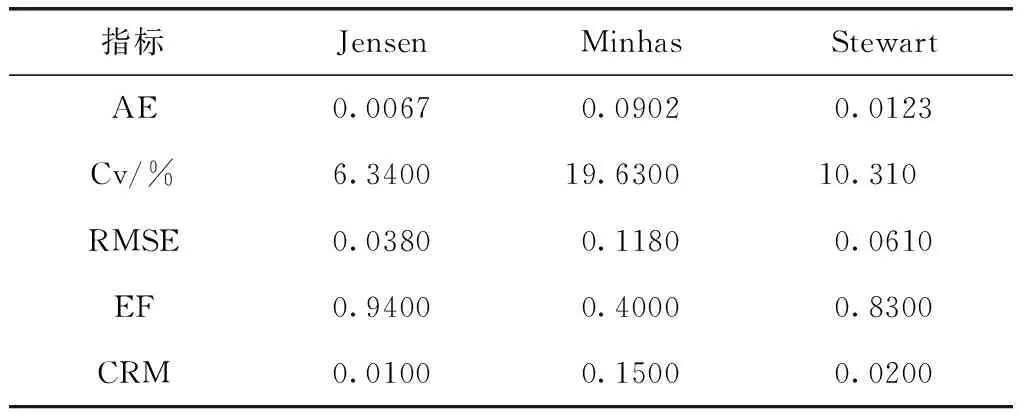
表4 模型模拟精度分析

3 结 论

(1) 比较各模型模拟大豆相对产量的效果先后排序为Jensen模型、Stewart模型、Minhas模型，Jensen模型模拟效果最好，Minhas模型模拟效果最差。

(2) 模型精度评价Jensen模型的平均误差(AE)、变异系数(Cv)和均方根误差(RMSE)分别为0.0067、6.34%和0.0380，均小于其他两种模型；而对于反映模型整体模拟能力的模拟性能指数EF，其值为0.94，大于其他模型。对残差聚集系数CRM进行对比分析表明，模型对于大豆相对产量模拟值偏高，与其他模型相比最接近于零。因此，建议黑龙江省甘南县大豆水分生产函数选用Jensen模型，可为该地区大豆非充分灌溉条件下的灌溉制度优化提供基础依据。