基于模糊控制的小区域交叉口群过饱和状态信号协调优化*

赵盼明 刘 钊 刘 玉 郭建华

(东南大学智能运输系统研究中心 南京 210096)

0 引 言

近年来，交通供需矛盾日益突出，仅仅依靠建设新的道路设施来缓解供需矛盾已不能妥善解决该问题。据调查，缺乏先进的交通管控技术是造成我国大部分城市道路通行能力没有被充分利用、道路拥堵的主要原因之一[1]。对城市交通的控制按照范围可以分为单个交叉口的信号控制、干线交通信号协调控制和区域交通信号相位协调控制[2]。城市区域路网中交叉口较为密集，各个交叉口之间相互影响，形成具有空间相关性和交通相关性的交叉口群[3]。交叉群过饱和状态，即交叉口群中多个交叉口交通量超过其容量，交叉口群处于交通流量大、状态不稳定、时空资源紧张、交通延误增加、排队溢出的状态。交叉口群在城市路网中广泛存在，但目前针对小区域交叉口群的过饱和状态信号协调控制研究较少，笔者以此作为研究对象展开相关研究。

国外针对小区域交叉口群信号控制的研究中，SCOOT是基于TRANSYT的一种自适应控制系统，具有处理过饱和状态交通的能力[4-5]；Shepherd[6]通过对适用于拥堵或过饱和条件下的交通控制方法，如OPAC,PRODYN,SAGA,SCATS和SCOOT等进行分析，探讨了以上控制系统处理拥堵问题的能力。Lee等[7]应用分布式协同模糊控制对交叉口群进行交通控制。Abu-Lebdeh等[8]结合动态控制算法和负效用函数，通过动态控制算法进行信号控制参数设计，利用负效用函数评测预设系统性能目标下，动态控制算法的相对性能，提出了在过饱和条件下动态评价交通管理策略的程序。当前常用的区域信号控制系统(如SCATS，SCOOT，OPACW，RHODES[9-11])，虽然功能基本完善，但在应用于我国交通流特征复杂的城市交通，尤其是针对我国区域交叉口群过饱和状态的交通协调控制，仍存在很多不足[12]。

在国内，区域交通信号协调控制的研究起步较晚。浙江浙大中控信息技术有限公司成功开发Intellific交通信号控制系统，总体技术达到国际先进水平，并在柳州、杭州等城市广泛应用。随后，各种人工智能研究方法如模糊控制、遗传算法、神经网络、粒子群优化算法等逐渐在交通控制领域得到广泛应用[13]。刘智勇等[14]提出一种基于改进免疫遗传算法的城市区域交通自适应协调控制；张辉等[15]将分布式Q学习运用到城市区域交通协调控制，提出了与区域交通协调相适应的奖惩函数与权值函数，并验证了该函数的有效性；孙超等[16]采用模糊控制方法对孤立交叉口的多相位模糊控制进行了一些研究，为了改善模糊控制器的效果，加入了自调因子进行优化；范立权等[17]提出了应用模糊逻辑的方法来优化交叉口的相位切换顺序，并进行了Paramics微观交通仿真，结果表明该算法能一定程度上提高车辆的平均速度；肖超[18]以区域交叉口各相位方向的排队长度为评价参数，建立模糊控制规则；张文泉和余立建[19]以交叉口平均车辆延误为评价指标，提出一种基于BP神经网络的区域多交叉口协调控制方法。

综上可知，国外的区域交叉口群协调控制发展已有一定的基础，在国内，利用人工智能算法对区域信号控制进行已经成为一种研究方向。但以往主要针对城市区域非饱和状态进行研究，对城市小区域交叉口过饱和状态下的协调控制研究较少，同时模糊控制算法在区域控制应用领域的研究中，国内学者多数选择单个输入变量设计模糊控制器，缺乏一定的可靠性，同时输入变量的模糊分集和隶属度函数的选择主要依据专家经验，缺乏一定的客观性。

笔者以小区域交叉口群过饱和状态为研究对象，通过模糊C均值聚类的方法，对各进口最大排队长度、平均行车延误进行模糊分集，根据聚类得到的隶属度矩阵，画出每个模糊集合的隶属度折线图，并依据折线图选择梯形隶属度函数作为输入变量的隶属度函数，然后根据区域交叉口不同进口道对区域内交通的影响，将区域进口道分为区域外进口道和区域内进口道，对区域外进口信号控制采取一级模糊控制器控制，对区域内进口道信号控制采取二级模糊控制器控制。最后根据综合控制规则，对区域交叉口群信号进行协调控制，以达到缓解过饱和交叉口群交通拥堵的目的。

1 过饱和交叉口群

交叉口群是指城市路网中具备以下2个特性的交叉口的集合：①空间相关性，即空间距离较小；②交通相关性，即交通流是动态变化且互相影响的[3]。交叉口过饱和状态即为交叉口交通量与交叉口通行能力的比值大于1的交通状态，文中交叉口群过饱和状态指小区域内多个交叉口处于过饱和状态，从而导致区域内其他交叉口的最大排队和行车延误受到影响，进一步导致区域内交通状况拥堵的状态。若小区域内交叉口群较长一段时间处于过饱和状态，区域内存在某个或某几个交叉口的排队长度较大，则会产生排队溢出，对临近交叉口交通造成影响，进一步影响区域甚至区域外围交通；同时行车延误是小区域过饱和交通状况评价的一个重要指标，过饱和状态交通越拥堵，车辆行驶延误就会越大。笔者将交叉口最大排队长度和行车延误作为交叉口交通状况评价指标，输入模糊控制器，通过调整各进口道绿灯时间，对区域交叉口群信号进行协调控制，达到减少排队和行车延误的目的。

2 基于模糊控制的过饱和交叉口群信号协调控制

2.1 模糊控制器设计

模糊控制器是模糊控制的核心部分，其主要内容是利用模糊语言来描述控制规则。模糊语言不像传统集合那样只存在“有”或者“没有”2种状态，它可以很准确的描绘事物的不确定性。根据不同进口道对区域内交通情况的影响，将区域交叉口群进口道分为区域内进口道和区域外进口道。区域内进口道，即车流流出区域的进口道，区域外进口道，即车流流入区域内部的进口道。针对区域外进口道和区域内进口道分别设计一级模糊控制器和二级模糊控制器。

2.1.1 一级模糊控制器

一级模糊控制器对区域外进口道绿灯时间进行调整控制。具体步骤为：输入区域外进口道最大排队长度，进行外进口道模糊推理，得出外进口道绿灯时间调整量，对交通控制方案进行调整，调整后的信号控制方案反作用于交通流，通过多次循环调整，对区域交叉口群交通状况进行优化。具体流程如图1。

图1 一级模糊控制器Fig.1 Level 1 fuzzy controller

2.1.2 二级模糊控制器

二级模糊控制器主要对区域内进口道信号控制进行调整。具体步骤为：输入区域内进口道的最大排队长度和行车延误数据，进行内进口道模糊推理，得出内进口道绿灯时间延长值，对交通控制方案进行调整，调整后的信号控制方案反作用于交通流，通过多次循环调整，对区域交叉口群交通状况进行优化。具体流程见图2。

图2 二级模糊控制器Fig.2 Level 2 fuzzy controller

2.2 模糊控制变量模糊集

选取最大排队长度和行车延误2项交通评价指标作为模糊控制算法的输入变量，选取绿灯时间调整量作为输出变量。为克服一般模糊控制中仅依据经验进行模糊集合划分的缺陷，本研究采用模糊C均值聚类的方法，对最大排队长度和行车延误数据集进行聚类分析，并根据聚类结果进行模糊分集，得到输入变量的模糊集合见表1和表2，输出变量模糊集合见表3。

表1 最大排队长度模糊集

表2 平均行车延误模糊集

交叉口各相位的绿灯延长时间，s。以5 s为最小绿灯延长时间，绿灯延长时间的模糊子集划分见表3。

表3 绿灯延长时间模糊集

2.3 隶属度函数及模糊规则

根据过饱和状态下车辆平均行车延误和最大排队长度的调查数据，将输入变量论域定为：{0～600}，将输出变量论域定为：{0～20}。根据模糊C均值得到的隶属度矩阵可知，每个模糊集合在隶属度为1处总表现为1段水平线，即输入变量在隶属度为1处不仅仅有唯一值，因此选取梯形函数作为输入变量的隶属函数(见图3)，同时选取三角形函数作为输出变量的隶属函数，见图4。根据输入输出变量隶属度函数，将模糊变量对应的具体隶属度值整理成表，如表4～6。

图3 输入变量的隶属度函数Fig.3 The membership function of the input variable

图4 输出变量隶属度函数Fig.4 The membership function of the output variable

根据模糊变量集合及隶属度函数，本文共制定25条模糊控制规则，具体如表7。假设交叉口某一进口道最大排队长度模糊集为VS，平均行车延误模糊集为VS，查表7可得，该进口方向绿灯延长时间模糊集为VS。

表4 最大排队隶属度

表5 延误隶属度

表6 输出变量隶属度

表7 模糊控制规则表

将模糊隶属度函数和模糊规则输入Matlab软件，分别建立一级模糊控制器和二级模糊控制器。对于一级模糊控制器输出的绿灯时间调整值，对相应的区域外进口进行绿灯时间减短，以减少进入区域的交通量；对于二级模糊控制器输出的绿灯调整值，对相应的区域内进口进行绿灯时间延长，以增大流出区域的交通量，从而减小区域最大排队长度与平均延误，改善整个区域的交通状况。由于绿灯调整时间小于3 s时，对交叉口交通状况影响较小，本研究仅对输出绿灯调整值大于3 s的相位进行调整，且规定同一相位累计调整值不大于20 s。

2.4 模糊控制算法流程

根据模糊控制器和模糊规则，制定模糊控制算法的具体流程。首先对区域初始交通信号控制方案进行微观仿真，计算区域外最大排队长度Lout、区域内最大排队长度Lin和区域内行车延误Din；将区域外最大排队长度Lout输入一级模糊控制器，将区域内最大排队长度Lin和区域内行车延误Din输入二级模糊控制器，并分别输出交叉口相位k第i次协调的绿灯时间调整值eki；若绿灯时间调整值eki大于3s，且相位k累计调整值Ski不大于20 s，则对该相位进行绿灯时间的调整；其中对区域外进口道进行绿灯时间的减少，对区域内进口道进行绿灯时间的延长。最后对调整后的控制方案进行仿真，根据调整前后仿真结果对比，分析评价区域交通优化效果。具体流程见图5。

3 基于模糊控制的区域信号协调控制实例

3.1 区域交叉口调查及数据处理

根据模糊控制算法及区域实际交通情况，交通调查内容主要有：区域各交叉口信号控制方案、各交叉口几何条件设施和各交叉口高峰期进口道车流量(分大小车型)。确定武汉徐东商业圈为研究区域，该小区域主要有四条道路组成，分别是徐东大街、友谊大道、秦园中路和团结大道。根据研究内容及实际区域交通情况，对徐东商圈4个交叉口进行调查，分别为：徐东大街-友谊大道交叉口、徐东大街-团结大道交叉口、团结大道-秦园中路交叉口、秦园中路-友谊大道交叉口。将徐东商业区4个主要交叉口依次标注为交叉口1，2，3，4，见图6。

图5 小区域交叉口群信号协调流程图Fig.5 Small area intersection group signalcoordination flowchart

将现场调查数据进行进一步处理，作为模糊控制优化和Vissim仿真的基础，交通数据具体处理步骤如下。

图6 区域交通平面图Fig.6 Regional traffic floor plan

1) 根据车型换算系数，将调查表中的左直右车流量换算为小汽车当量，再将换算后的15 min小汽车交通量换算为小时交通量。

2) 根据调查区域各交叉口信号配时调查数据，绘制各交叉口信号配时表。

3) 根据交叉口几何条件设施及交叉口进口道简图，绘制区域各交叉口进口道平面图。

4) 绘制调查区域整体平面交通图，为Vissim仿真路网建设提供底图。

以友谊大道-徐东大街交叉口为例，进行调查结果的展示，调查时间为3月11日08：35—08：50，具体交叉口数据处理结果为交通调查表(见表8)和信号配时表，见表9。

表8 友谊大道-徐东大街交通调查表

注：1.根据CJJ37—2012《城市道路设计规范》[20]，大型客车车辆折算系数为2；2换算公式：小汽车当量=(小车数+2×大车数)×4。

表9 友谊大道-徐东大街交叉口信号配时

本研究根据交叉口交通几何条件和信号配时方案，分别计算小区域内各交叉口进口道通行能力，并对多个区域外进口道输入大于进口道通行能力的交通量，使得该小区域交叉口群处于一种过饱和的交通状态，并利用模糊控制对交叉口群进行信号协调控制。

3.2 小区域交叉口群仿真

1) 底图导入及车道铺设。将区域平面图5作为仿真底图导入Vissim软件。

2) 路径决策及信号灯组设置。根据调查数据，交叉口每1个进口方向车流按实际所占车流量比率分配至左直右3个方向，对未设专用左转或设有混合车道的进口，按合理比例划分；交叉口信号灯组根据调查信号相位表设置。

3) 道路检测器设置。区域交通仿真需要在路网中设置行程时间检测器和排队计数器[23-25]。本文在4个交叉口各进口方向分别设置行程时间检测器46个，排队计数器46个。其中，行程时间检测器设置在进口处，可采集起终点的行程时间与行车延误，进而得到交叉口的通行时间。排队计数器设于距离信号灯50 m左右的位置，用于检测排队等待的车辆数和排队停车数。

4) 模型运行调整。完成Vissim仿真路网构建并运行，观察仿真过程中交通信号灯及各方向车流，对信号相位不出现全红时间、个别车道无车流、车辆消失等错误进行修改和调整，以确定交通仿真符合实际交通过程。最后对正常的区域路网仿真运行3 600 s，导出区域各交叉口的行车延误和排队长度数据。

3.3 交通控制现状仿真分析

根据交通区域路网仿真步骤，对武汉徐东商业区域路网进行仿真。具体仿真结果数据见表10。

表10 最大排队和行车延误表

由行车延误表和排队长度表可知：区域最大排队总长度为4 735.5 m，最大排队平均值为4 735.5/30=157.85 m,区域总延误为2 899.9 s，延误平均值为2 899.9/30=187.09 s，即交叉口群最大排队长度的平均值大于150 m，超出进口道长度，延误平均值大于100 s，大于1个周期的进口道绿灯时间，则该交叉口群整体的最大排队和平均行车延误较大，现状交通信号控制方案不能很好地满足该时刻交通量需求，应对该区域交通信号进行协调控制。

3.4 模糊控制信号协调算法应用及仿真

3.4.1 交叉口群绿灯时间调整

根据徐东区域现状仿真结果，对现状交叉口群的最大排队长度和行车延误数据进行分析，根据模糊规则，分别对区域内外的进口相位进行绿灯时间的调整，直至某一进口道绿灯时间累积调整值大于20 s为止。具体调整见表11，其中交叉口3北进口左转相位绿灯延长时间累计值：7+7+6=20 s，则对于第5次调整不再进行，区域信号协调停止。

表11 绿灯时间调整表

3.4.2 模糊控制方案仿真分析

根据具体绿灯时间调整方案，对模糊控制协调后的方案进行多次仿真，输出仿真结果整理成表12和表13。对最终调整方案的延误进行分析，区域15个内进口道中，对于1 h的平均行车延误数据，12个进口道延误小于100 s，其中有两个进口道数据大于100 s小于120 s，绿灯多次调整后，该区域延误有所改善。其中交叉口3的北进口左转方向延误较大，为440.4 s，分析该进口道仿真运行过程可知，该方向左转车辆需要让行对向直行车辆，而对向直行车流较大，且南北进口左转和直行为混合相位，即使左转相位绿灯时间延长，仍不能很好的减少左转车辆延误。最终调整方案最大排队长度中，区域15个内进口道中9个进口道最大排队长度小于150 m，4个进口道最大排队长度大于150 m小于200 m，其中交叉口3北进口直行和北进口左转车辆最大排队长度分别为202.5 m和202 m，其原因为北进口直行车流较大，同时左转车辆需要让行直行车辆，导致其在左转等待区排队较多。

3.5 方案对比分析

由调整方案延误表和最大排队长度表可知，小区域交叉口群中区域内进口道每次调整后数据显示如表，研究区域共分为区域内进口道15个，区域外进口道15个。经4次模糊控制协调后，区域内进口中11个内进口行车延误相应减少，减少量总量为385 s，11个进口道平均减少量为35 s，区域内进口中12个内进口方向的最大排队长度相应减少，排队减少总量为998.5 m，12个进口道的最大排队长度平均减少量为83.2 m。

表12 调整方案交叉口行车延误表

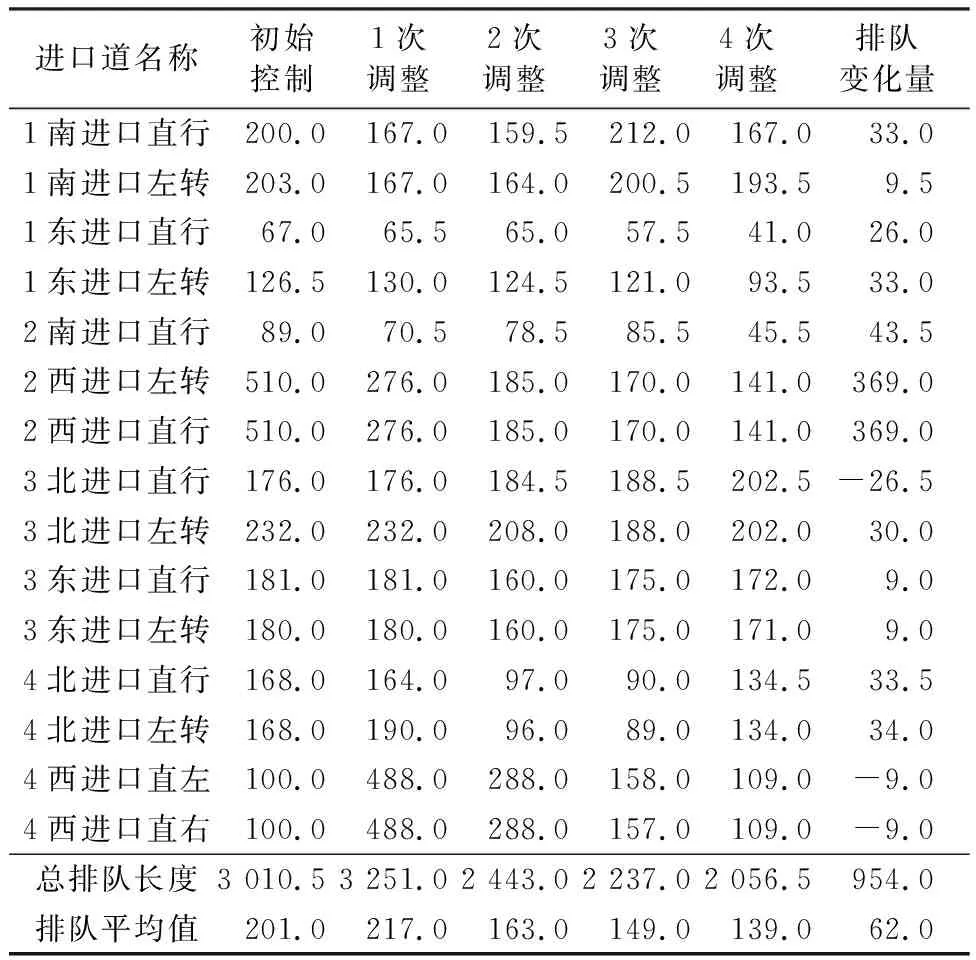
表13 调整方案交叉口最大排队长度表

对比每次调整后最大排队长度和行车延误，经过4次信号协调，区域内进口道总延误和总排队长度逐渐减少，平均延误由最初的110.62 s减少为87.94 s，延误减少量为22.68 s；最大排队长度平均值由最初的201 m减少为139 m，减少了62 m。协调结果表明，针对交叉口群由非饱和到过饱和状态的小区域信号协调，本研究具有比较好的效果。

4 结束语

模糊控制在交通信号控制领域已经成为一个重要发展方向[21-22]，以徐东区域4个交叉口组成的小区域交叉口群为研究对象，将交叉口群各进口道的最大排队长度和平均行车延误作为模糊控制的输入变量，分别对最大排队长度和延误进行模糊C均值分类，得到输入变量的模糊集合中心值和模糊隶属度矩阵，根据模糊聚类中心值对最大排队长度和延误进行模糊分集，并根据模糊矩阵数据选择梯形模糊隶属度函数作为输入变量的隶属度隶属函数；采用减少区域交通流入、增加区域交通流出的思路制定模糊规则，针对区域外进口道和区域内进口道，分别设计一级模糊控制器和二级模糊控制器；通过将武汉徐东区域进行交通调查，对小区域中多个交叉口输入过饱和交通量，使其达到交叉口群过饱和状态，采用模糊控制对该交叉口群信号进行多次协调优化。

该模型从整个区域的交通状况出发，通过两级模糊控制器，对区域交叉口群内外进口信号进行控制，无需建立精确的数学模型，较好地适应交通系统复杂性，随机性的特点。本文在模糊控制中的创新之处如下：

1) 输入变量模糊分集和隶属度函数的选择。本文首先采用模糊C均值方法对2个输入变量的精确值进行分类，而不是仅根据经验进行模糊分集，同时根据模糊隶属度矩阵进行模糊隶属度函数的选择，所选择的梯形隶属度函数符合输入变量的实际隶属度。

2) 模糊规则的制定。综合分析区域交叉口群的交通状况，在过饱和状态下，采取减少交叉口群车流输入增大车流输出的策略，在一定程度上控制了交叉口群排队溢出的趋势，缓解了区域交通拥堵。

研究中存在的不足之处：①仿真过程中，仅考虑机动车因素，缺少非机动车和行人的仿真；②仅针对一种过饱和状态进行研究，后期需要针对不同的过饱和状态，分别采用模糊控制方法进行对比研究，进一步验证方法有效性。