驾驶行为特性对道路通行能力影响的量化研究*

黄天伊 周晨静 王 益

(1.北京工业大学北京市交通工程重点实验室 北京 100124；2.北京建筑大学土木与交通工程学院 北京 100044)

0 引 言

道路通行能力是交通工程领域重要研究内容，以美国交通研究委员会为首的研究团队吸收新近研究成果，于2010年更新并出版第五版《道路通行能力手册》Highway Capacity Manual，以下简称《HCM手册》，进一步完善道路通行能力研究内容与方法。《HCM手册》将道路通行能力影响因素分为道路条件、交通条件及控制条件3类[1]，而对驾驶行为特性影响考虑较少，只是给出驾驶人总体特征系数表征驾驶员对道路设施熟悉程度，用于分析和计算通勤区域与旅游休闲区域道路通行能力，取值范围为0.85～1.0。

然而，在人、车、路构成的道路交通系统中，人是最关键也是最敏感的因素，驾驶人驾驶行为特性对通行能力的影响在近年逐渐得到学者们的认可和重视。Lownes等[2]利用Vissim仿真分析快速路基本路段通行能力对驾驶员微观驾驶行为参数的敏感性；Yannes等[3]进一步研究驾驶员微观驾驶行为参数组合对快速路通行能力影响，并分析其对通行能力的影响机理；Chu Chileung[4]等以交织区不同位置、不同驾驶行为特性参数为依据将驾驶人驾驶状态分为放松状态、正常状态、冒险状态、过激状态4种类型，不同状态有着不同的微观运行参数，由此分析不同驾驶人特性对交织区通行能力的影响；Yang Xiaobao和Zhang Ning[5]利用实测数据分析得出：由于车辆换道行为的影响，路段通行能力增长与车道数量增长并不成正比关系；Rong Jian等[6]应用驾驶模拟舱技术对驾驶人微观行为特性进行研究，将驾驶人分为保守型、一般型、冒险型3种类型，并分析不同类型驾驶人对宏观交通流特性的影响，研究发现：与保守型和一般型驾驶人相比，冒险型驾驶人更趋向于选择较小跟车间距，在车流中表现出较为频繁的换道行为，并且由冒险型驾驶人组成的车流在基本路段运行时有着较高的交通流率，其交通流稳定性却最差。

以上研究均证实驾驶人驾驶行为特性对道路宏观交通流特性及通行能力有着重要影响，然而目前仍缺乏驾驶行为特性在道路通行能力分析计算过程中的量化研究。笔者在前人研究基础上，将驾驶人分为冒险型、一般型、保守型3种类型，根据已有模型标定参数，提出以仿真实验为基础的驾驶行为对道路通行能力影响系数的量化分析方法，研究成果可为通行能力科学计算提供依据，同时对提高实际道路通行能力具有十分重要的意义。

1 实验设计

1.1 仿真场景建立

仿真技术是通行能力研究的主流方法之一。Roess等[7]应用实测数据证实了Vissim仿真软件在仿真模拟微观驾驶行为特性，尤其是交织区车流运行特性上的有效性。本研究采用Vissim 5.3进行仿真模拟，通过构建基本路段行为仿真场景和交织区行为仿真场景，测算不同驾驶行为特性对宏观交通流及设施通行能力的影响。

基本路段仿真实验通过构建单车道、双车道、3车道及4车道的仿真场景,模拟车流由自由流到拥挤流运行过程。其中，单车道仿真实验用来研究驾驶人跟驰行为特性对通行能力的影响；随着车道数增加，驾驶人自由换道几率增加，多车道仿真实验用来研究自由换道行为对通行能力的影响。仿真场景参数设置为：路段长度500 m，车道宽3.5 m，限速80 km/h的快速路车流运行状态，车辆期望运行车速服从平均车速为75 km/h、标准差为2 km/h的正态分布，车流由标准小汽车组成。

在基本路段行为仿真基础上，构建快速路交织区行为仿真实验场景研究驾驶人强制换道行为对设施通行能力的影响。仿真场景参数设置为：主线3车道，交织区长度500 m，限速、车辆期望运行车速、车流车辆类型等其他参数设置同上。

1.2 驾驶行为参数设置

在文献[4]的基础上，Rong Jian等[6]利用模拟驾驶实验把驾驶员分为稳定型、冒险型和适中型3类，标定了符合我国驾驶人驾驶习惯的微观行为模型参数，聚类结果能够较好体现驾驶员个体差异性。本研究结合文献[4]和文献[6]对驾驶人驾驶行为特性描述和微观建模参数基础，将驾驶人分为冒险型、一般型、保守型3种类型，设置对应仿真实验微观驾驶行为参数见表1。

1.3 仿真实验过程

对于微观交通仿真实验，随着输入流量的增加，交通流状态经历自由流-稳定流-拥挤流3种状态的转变，交通流率随之经历逐渐增加-趋于稳定-迅速下降3个过程。不同驾驶行为参数设置条件下，当交通流率达到稳定状态而不随输入流量增加而增加时，认为设施处于满负荷状态，此时即可得到相应驾驶行为特性影响下的道路通行能力值。

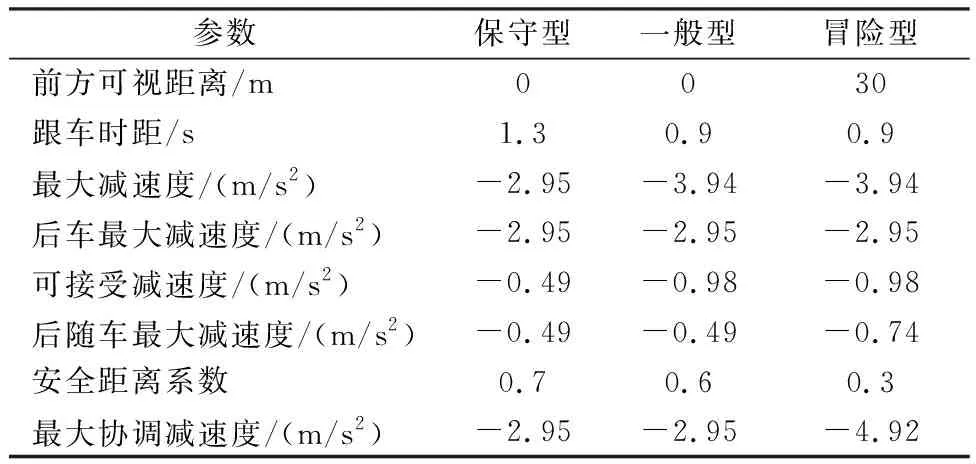
表1 不同类型驾驶人驾驶行为参数

注：数据来源于文献[4]和文献[6]。

基本路段行为仿真实验输入交通流量由1 000 pcu/h增长至3 000 pcu/h，每次增加100 pcu/h；每次仿真条件取5，35，65，95，125，155，185，215，245，275共10个随机种子。仿真实验共进行2 100次，过程中记录基本路段平均运行车速、小时流率及自由换道次数。交织区行为仿真实验交通流量以2 000 pcu/h为基数、以5%为增长率增至8 232 pcu/h；交织流量比从0.1到0.4变化，其中由匝道至主线车流量等于由主线到匝道车流量；每次仿真条件取5，35，65，95，125，155，185，215，245，275共10个随机种子。仿真实验共进行1 200次，过程中记录交织区平均运行车速、平均车流密度、小时流率及强制换道次数。

2 不同驾驶行为对通行能力的影响分析

2.1 基本路段通行能力分析

2.1.1 跟驰行为对通行能力的影响

按照上节所述建模方案执行基本路段行为仿真，得到不同类型驾驶行为、不同车道数条件下的输入流量与流率散点图，如图1～3。由图中看到，当输入流量在2 500～3 000 veh/(h·lane)范围内时，设施流率基本趋于稳定状态。取此范围内的交通流率做统计分析，得到不同驾驶行为、不同车道数量条件下的设施通行能力值，见表2。

在单车道仿真场景中，由于只存在跟驰行为而不存在换道行为，冒险型驾驶人与一般型驾驶人驾驶行为具有相同的跟驰行为参数和换道行为参数，2种类型驾驶行为参数设置条件下车道具有基本相同的通行能力值，约为2 250 veh/(h·lane)；而保守型驾驶人更趋向于保持较远的跟车距离，占用更多的道路空间资源，在保守型驾驶行为参数设置条件下车道通行能力值明显降低，约为1 900 veh/(h·lane)。

图1 冒险型驾驶人参数设置条件下的输入流量-流率散点图Fig.1 Input-Output flow scatter diagram under the condition of risk driver parameter setting

2.1.2 自由换道行为对通行能力的影响

不同类型驾驶人具有差异性的换道行为参数。由表2可知，多车道仿真场景的稳定流状态下，多车道道路中单车道通行能力与对应单车道路段通行能力值基本相同，即不同驾驶行为参数条件并未对道路通行能力产生明显影响。

为进一步探究自由换道行为对通行能力的影响机理，做多车道仿真环境中道路输入流量与换道次数关系散点图，如图4。由图4可见，随着输入流量及车道数量的增加，在达到稳定流状态前车流换道频率均表现为不同程度的增加。其中，在整个仿真过程中，冒险型驾驶人的换车道频率最高、换道次数峰值达到500次以上，一般型和保守型驾驶人换道次数峰值在400次以上，一方面说明冒险型驾驶人为了选择更快的速度而变换车道，侧面验证了驾驶人参数设置与驾驶行为特征描述的对应性；另一方面频繁的变换车道不仅为交通安全带来隐患，而且也会对交通流的稳定性产生影响。进而，选取输入流量在0～2 000 veh/(h·lane)范围内，即自由流状态下道路输入流量与道路交通流率进行回归分析，回归结果见表3。

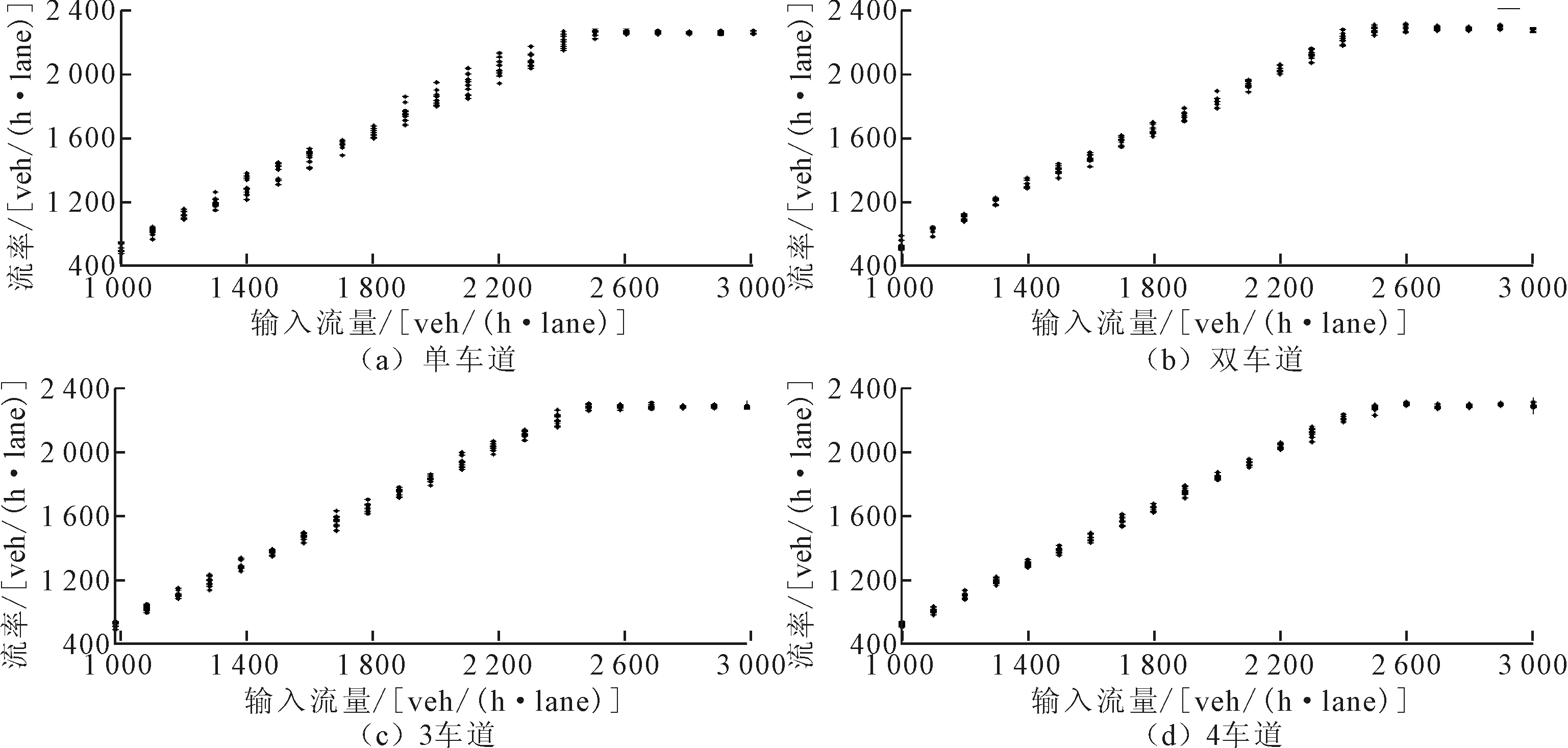
图2 一般型驾驶人参数设置条件下的输入流量-流率散点图Fig.2 Input-Output flow scatter diagram under the condition of general driver parameter setting

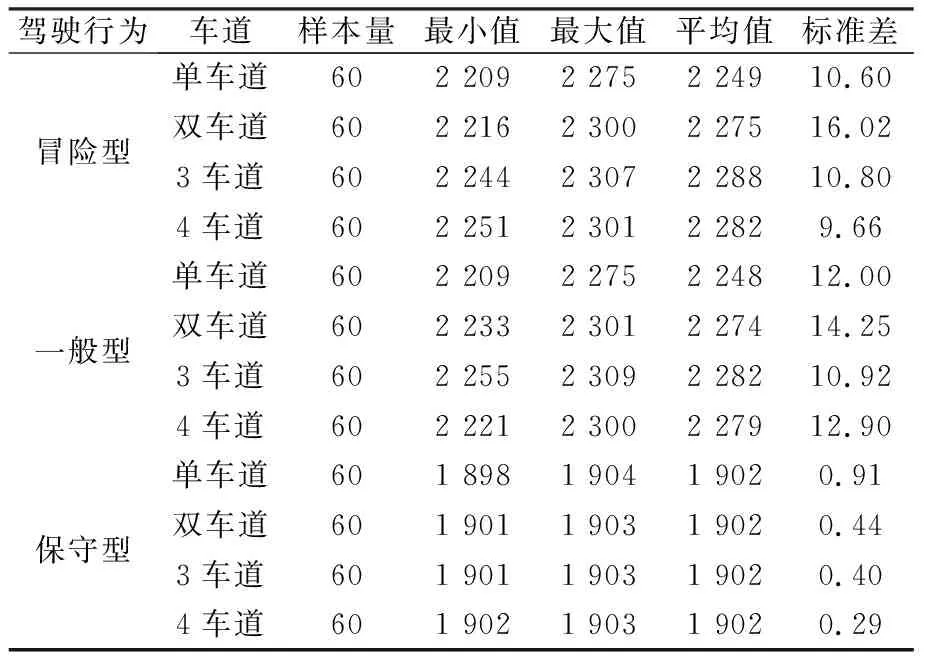
表2 不同驾驶行为参数设置条件下单车道通行能力值统计性描述

表3 自由流状态下输入流量与输出流率回归结果

根据回归结果可以看出，在不同驾驶行为条件下，随车道数量增加，输入流量与道路交通流率的回归方程系数均逐渐增大，即在道路交通流中自由换道行为可以提升道路资源利用率，促使车流由自由流运行状态更快地达到稳定流运行状态。

根据基本路段仿真结果可以得出以下重要结论：不同跟驰行为特性对道路通行能力有着明显影响；在相同驾驶行为设置参数条件下，道路车流在自由流运行状态中，车辆自由换道行为可以提升道路空间利用率，促使车流运行更快向稳定流运行状态转变，而在稳定流运行状态中，车辆自由换道行为受到限制，对稳定流运行状态并不产生影响。

2.2 交织区通行能力影响分析

交通流密度-速度关系是交通流状态的直观体现。为了分析不同类型驾驶人强制换道行为对道路通行能力的影响，仿真得到不同交织流量比条件下，不同类型驾驶人对应的车流密度与车流平均运行车速散点图，见图5。

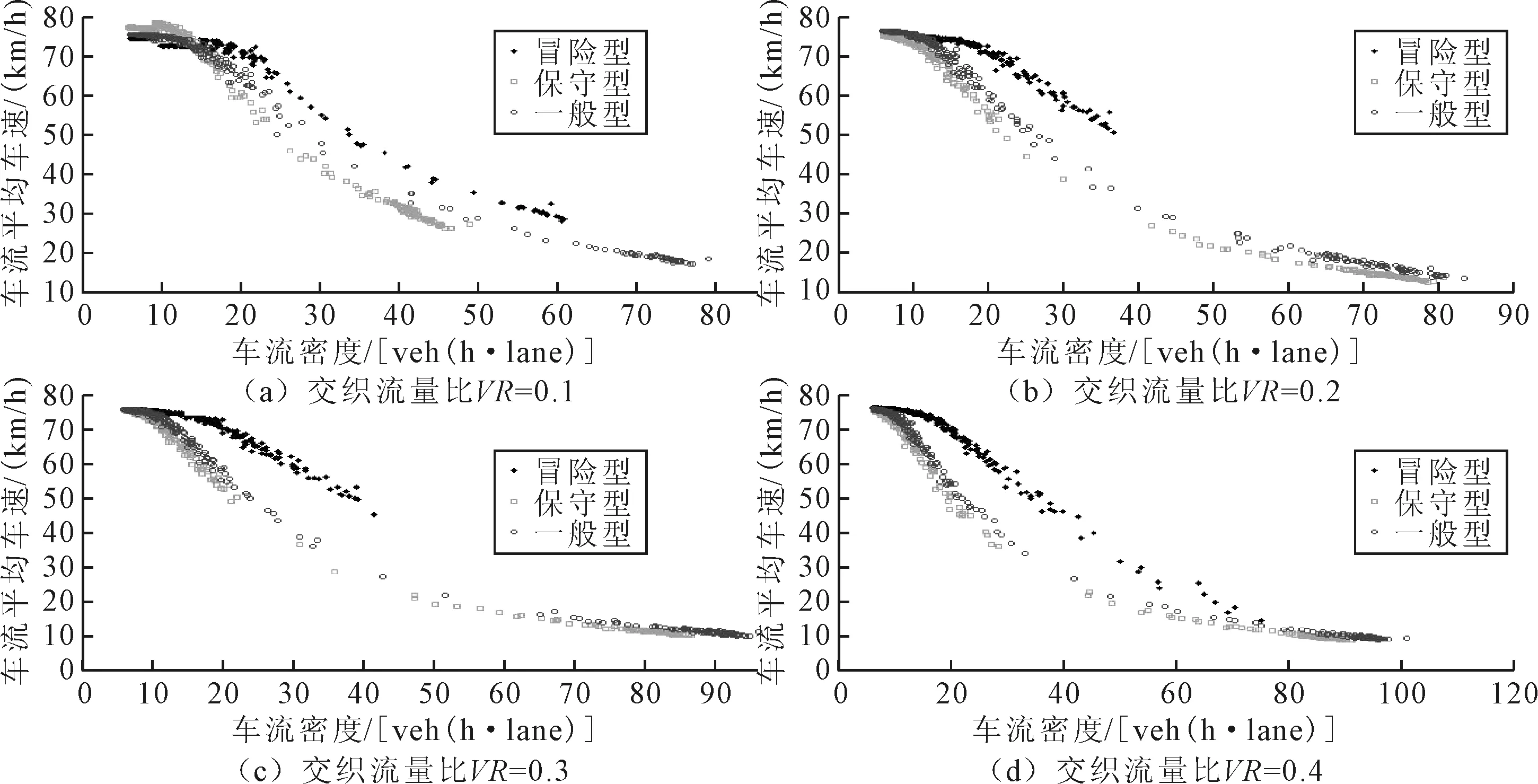
图5 不同交织流量比条件下交织区车流密度-车流平均运行车速散点图Fig.5 Density-speed of flow scatter diagram of interleaving area under the condition of different interlaced flow ratio

对于车流密度与速度关系的研究，有Greenshield的线性关系模型、Greenberg的对数关系模型、Underwood的指数关系模型等[8]。根据密度-速度散点图所示趋势，研究应用“L-S曲线”模型对数据进行回归分析，见式(1)。

S=a×eb×D2+c×ed×D

(1)

式中：S为速度，km/h;D为密度，veh/(km·lane);a，b，c，d为回归系数。回归分析结果见表4。

随着车流量增加，道路交通流经历自由流-稳定流-拥挤流3种状态的变化，在该变化过程中车流密度不断增加。当车流密度大于临界车流密度时，车流速度会急剧下降，车流运行状态由稳定流向拥挤流转变。使以上回归方程二阶导函数为零，可求出不同类型驾驶人驾驶行为参数设置条件下交通流由稳定流状态向拥挤流状态转变的临界密度值，结果见表5。其中，当交织流量比为0.4时，大量交织行为严重干扰交织区运行，车流较早进入拥挤流状态，临界密度值无法计算。

表4 密度-流量关系回归结果

由结果可知，3种类型驾驶行为参数设置条件下，交织区稳定流向拥挤流状态转变临界密度均随交织流量比增加而减少，即交织区通行能力随交织流量比的增加而减少，强制换道行为对交织区通行能力有着重要的影响。

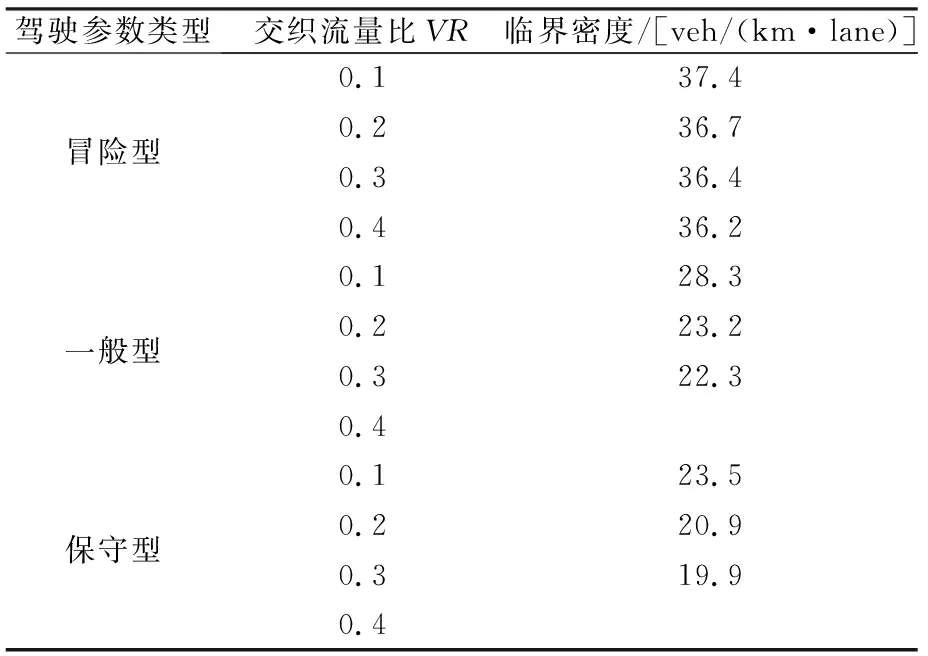
表5 临界密度计算值

为进一步分析不同类型驾驶人强制换道行为对交织区通行能力的影响，研究以速度-密度-流量公式(见式2)计算不同交织流量比条件下交织区通行能力，计算函数曲线见图6。

V=S×D

(2)

式中：V为流率，veh/(h·lane)；S为速度，km/h；D为密度，veh/(km·lane)。

由图可知，在相同交织流量比、不同驾驶人设置参数条件下，道路通行能力差异明显，冒险型驾驶人对应通行能力远大于一般型和冒险型驾驶人；在相同驾驶人设置参数、不同交织流量比条件下，道路通行能力随交织流量比增加而减小，但并非线性减小。

根据交织区仿真结果可以得出以下结论：驾驶人强制换道行为及换道次数共同影响道路交通流的运行，进而对道路通行能力产生显著影响。不同驾驶行为参数及换道次数条件下，交通流由稳定运行状态向拥挤运行状态转变具有不同的临界密度值，即道路设施具有不同通行能力；而在相同行为参数、不同换道次数条件下，道路通行能力随换道次数增加而非线性减少，说明强制换道行为在不同流量条件下对交通流运行影响不同。

3 驾驶行为特性量化分析

根据前文分析可知，不同驾驶人驾驶行为特性体现在跟驰及换道行为参数有所差别。其中，跟驰行为特性对交通流产生直接影响，跟车时距越大道路通行能力越小；自由换道行为虽可以提升道路设施空间利用率，但对道路通行能力没有明显影响；强制换道行为与换道次数共同影响道路通行能力。研究以未经驾驶人因素参数修正的道路通行能力为基准通行能力，结合不同驾驶行为对道路通行能力影响，提出驾驶行为特性量化方法。

首先确定道路设施单车道基准通行能力为C0，对于不同驾驶人跟驰行为特性导致道路通行能力变化，可以以不同驾驶行为参数设置条件下直行车流通行能力除以基准通行能力进行量化

(3)

式中：fti为第i类型驾驶人跟驰行为特性修正系数；Ci为第i类型驾驶人行为参数设置条件下单车道通行能力，veh/(h·lane)；C0为单车道基准通行能力，取2 200 veh(h·lane)；i为驾驶人类型：冒险型、一般型、保守型。

对于不同驾驶人强制换道行为特性导致道路通行能力变化，研究提出换道因子(LC)的概念作为每次强制换道行为对设施通行能力的折减系数，结合驾驶人类型及交织流量比量化不同驾驶人强制换道行为特性对道路通行能力的折减，具体计算方法如下

(4)

(5)

对于本次仿真研究，结合表2数据可以得出驾驶人跟驰行为特性修正系数(见表6)，该系数用于基本路段通行能力分析。

结合表2和图6数据可计算不同类型驾驶人在特定交织流量比条件下的换道因子，计算结果见表7，可用拉格朗日插值方法计算表格中未列出换道因子数。

表6 驾驶人跟驰行为特性修正系数表

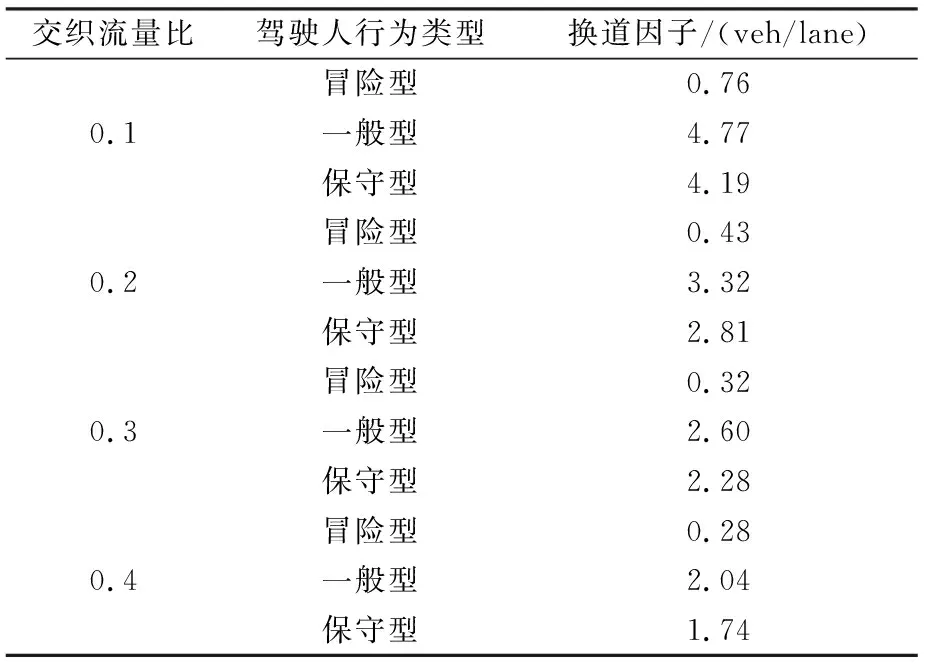
表7 换道因子计算表

由此可计算得出驾驶人在不同换道流量条件下，强制换道行为修正系数(见表8)，该系数可用于交织区通行能力分析。由表中可知，通过划分不同驾驶人开展仿真研究，相较于HCM手册中的驾驶行为总体折减系数，本研究提出的修正系数进一步细化区分了不同驾驶行为特性的影响程度，表征为差异化的修正系数，对于通行能力分析科学性的提升具有重要意义。

表8 驾驶人强制换道行为特性修正系数表

4 结束语

笔者基于驾驶行为特性研究，提出了驾驶行为特性对通行能力影响的量化修正方法：以微观仿真方法为手段，搭建针对性仿真场景模拟不同驾驶行为条件下车流运行状态，以交通流3个参数变化关系为分析内容，研究了不同驾驶行为对宏观交通流特性影响并确定设施通行能力，最后以道路基准通行能力为标准计算不同驾驶行为特性对通行能力影响的修正系数。研究细致探究了不同驾驶行为对宏观交通流及道路通行能力的影响，所建立的驾驶行为特性量化方法具有针对性和适用性，可为道路设计和交通管理提供一定的决策支持。