几种电力线绘制方法总结

杨 宁，梅中磊

（兰州大学信息科学与工程学院，甘肃兰州730000）

0 引言

电力（场）线即为直观表示空间电场分布而人为引入的一簇有向曲线，其起于正电荷，止于负电荷，曲线上每一点的切线方向即该点的电场强度方向，某点曲线的疏密度表示该点电场强度大小。电力线对理解电磁场有重要的辅助作用，可利用Matlab强大的计算功能进行电力线绘制。下面介绍四种基于Matlab的电力线绘制方法。

1 streamline函数绘制电力线

以两点电荷q1，q2系统为例，场点P（x，y）的电势可表示为（不考虑系数q／4πε）［1］

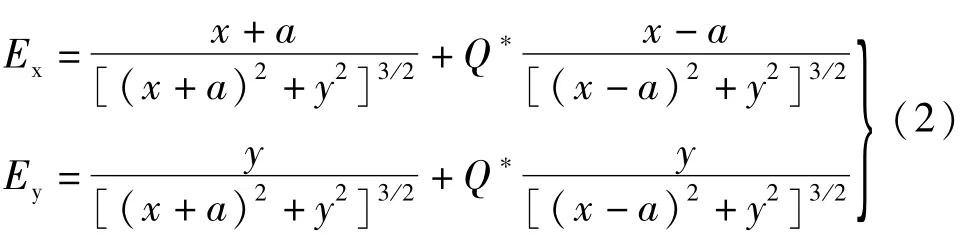
利用 Matlab 流线图绘制函数 streamline（x，y，u，v，sx，sy）绘制电场（Ex，Ey）［2］。（x，y）为矢量（u，v）的坐标，由网格函数 meshgrid生成；（sx，sy）为流线起点。场强分量Ex，Ey由梯度函数［Ex，Ey］＝ gra-dient（-U）得到。因电力线起于正电荷，止于负电荷，当其起始点距电荷很近时，认为各电力线绕电荷均匀分布。以一固定角度为间隔，设定电力线在正、负电荷周围的起点坐标。对电场矢量（u，v），若电力线从正电荷出发，则取为［Ex，Ey］；若从负电荷出发，则取［-Ex，-Ey］（负号表示二者反向）。图1为两点电荷系统分别在等量同号、等量异号、异量同号、异量异号时的电力线分布，异量时Q*＝2。

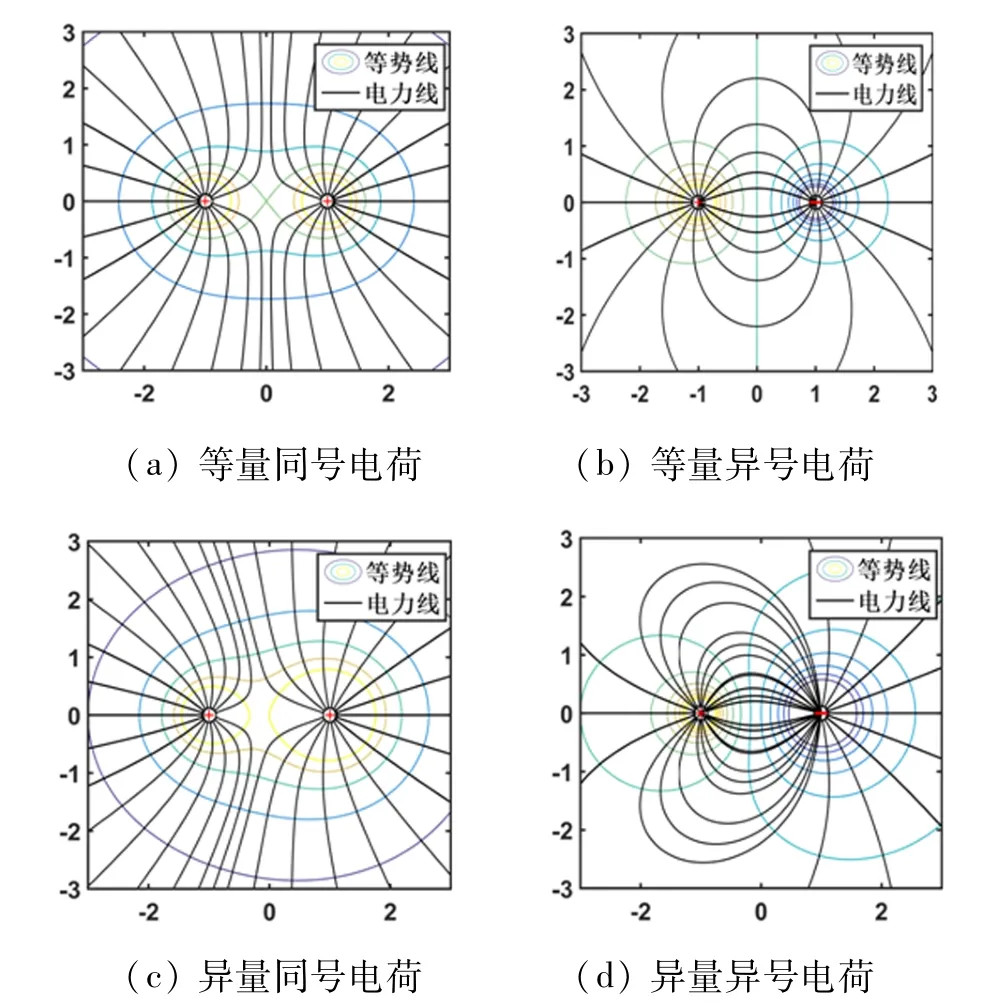
图1 streamline绘制两点电荷电力线分布

2 数值求解电力线方程以绘制电力线

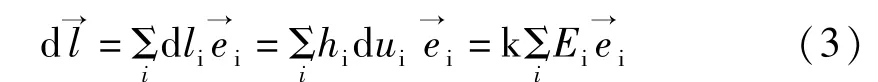
消去k，得电力线微分方程如下［2］：

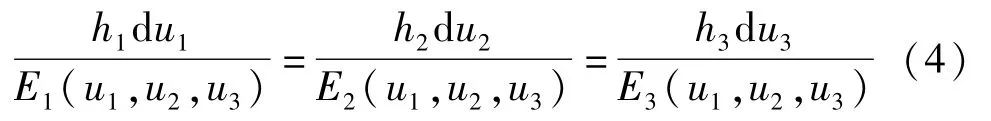
其中，h1，h2，h3为度规因子，坐标变量u1，u2，u3决定于正交曲线坐标系的具体形式。上式在直角坐标系中可写为 dx／Ex＝ dy／Ey＝dz／Ez＝dt，即有：

式（5）即为以t为参变量的一阶常微分方程组，该式在Matlab中可用如下函数描述：

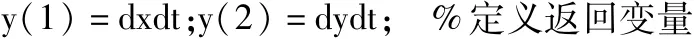
利用 Matlab的 ode45函数对式（5）进行求解［3］。ode 系列包括 ode23，ode45，ode15s 等，求常微分方程的数值解时首选ode45函数，用法如下：

odefun为函数句柄；tspan为参数的变化区间；y0为初始位置向量；T为位置列向量对应的时间点；Y为返回对应T的最终位置列向量（即空间横纵坐标值）。再利用 plot（Y（：，1），Y（：，2））绘制电力线。

以两等量同号点电荷为例，每个绘制起始点对应一条电力线；以每个电荷为中心，间隔角2π／k画k条电力线，遍历这2k个起点（即执行ode函数2k次），最终得到2k条电力线。图2为两等量同号和等量异号电荷的电力线分布。（a）等量同号电荷 （b）等量异号电荷图2 ode45函数绘制两点电荷电力线分布

3 解析求解电力线方程以绘制电力线

两点电荷系统如图 3 所示［4］。设点 P（x，y）、点P′（x′，y′）位于同一电力线上，使其连线 PP′绕x轴旋转一周，得到面SPP′。

图3 两点电荷系统

设S1与S2分别为平面x，x′被SPP′截取的两个圆面。考虑由S1和S2及SPP′构成的封闭曲面（设封闭曲面内电荷为零），由高斯定理SPP′的通量满足则以x轴正向为参考方向，S1，S2满足下式（S1与S2方向相反）：

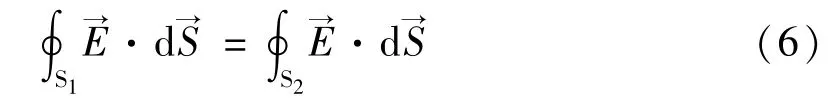
由电场强度叠加定理，两离散电荷电场：

对任意的（x，y）成立，其中C为常数。同理，当封闭曲面内电荷不为零时，系统电力线方程与式（8）相同［4］。式（8）中，以固定步长改变C，可得到一系列电场值，再利用ezplot函数，得到的两等量异号电荷电力线分布如图4（a）所示。式（8）也可由函数contour（x，y，z）实现，结果见图4（b）。

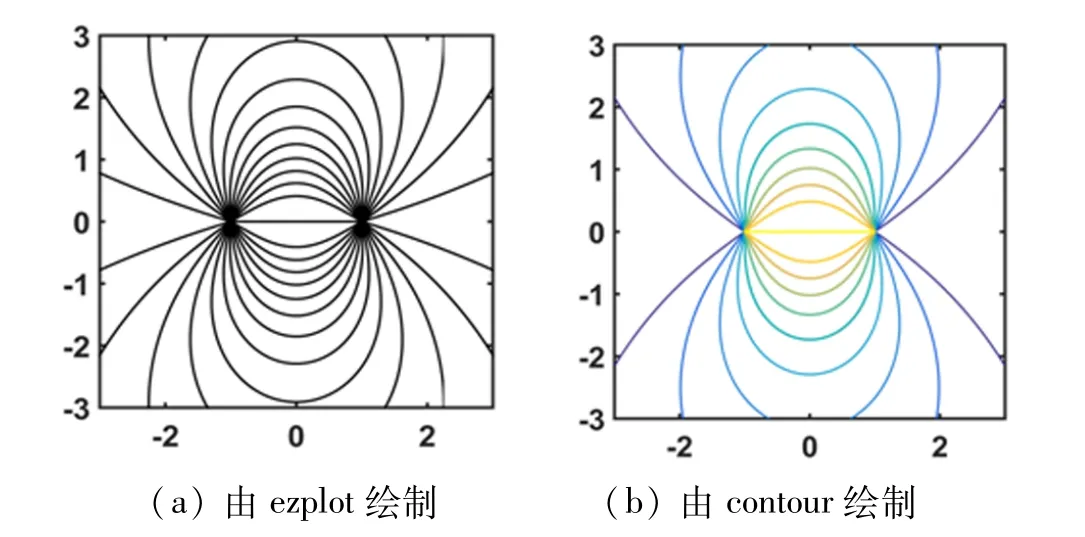
图4 由电力线方程绘制两点电荷电力线分布

4 quiver函数向量场绘制

4．1 两点电荷系统电力线举例

二维向量场绘制函数 quiver（x，y，u，v）用箭头表示矩阵（x，y）的各点矢量（u，v），一般配合 meshgrid和gradient函数使用，函数gradient产生近似梯度，函数meshgrid生成网格采样点。（x，y）可看做在xoy平面内对坐标进行采样得到的坐标对。对两点电荷系统，利用quiver绘制电力线方法同streamline，且无需设定起始点。图5为其绘制结果，纵向实线为contour绘制的等位线，箭头为quiver绘制的各点矢量电场。

图5 等量异号点电荷电力线分布

4．2 quiver函数绘制波导端口电力线分布

以圆波导为例，用quiver函数绘制波导端口电力线。由参考文献［5］得圆波导TM和TE波的场分量表示式。因只绘制端口电力线，故仅考虑Er和Eφ，绘制时注意将其转化为直角坐标系下的形式Ex和Ey。图6所示为圆波导中TE01和TM11模的电力线分布。

图6 圆波导电力线分布举例

5 结语

在Matlab默认精度（小数点后32位）下比较本文所列四种电力线绘制方法的运行速度。对于两点电荷系统的电力线绘制，quiver函数法耗时最短，仅约 0．06 s；其次为 streamline 函数法，用时约 0．35 s；再则为利用ode45函数的数值法，用时0．87 s；而解析法耗时最长，用时约2．21 s。因quiver函数法和streamline函数法程序简单，运行速度快，故常用这两种方法绘制两点电荷间的电力线分布。而在给定电力线条数和范围时，应考虑解析法或数值法，其中，解析法设定的是电场的横纵坐标范围，而数值法设定的是电力线距绘制起点的距离。对于解析法，因电荷分布复杂时较难得到系统的电力线方程，且其程序运行耗时长，故多用数值法绘制其电力线分布。 总之，上述方法各具优势，实际中应根据要求选择使用。