确定性横向迁移中液固两相流的三维格子玻尔兹曼模拟*
2018-10-11彭浩宇陈英怀郭钟宁黄志刚
彭浩宇,陈英怀,郭钟宁,黄志刚
(广东工业大学机电工程学院,广东广州 510006)
0 引言
利用微流控芯片对微观物质进行快速分离是一种前景广阔的新兴技术,可用于生物医疗、环境检测和精细化工等科技领域[1]。近十几年发展起来的确定性横向迁移技术(Deterministic Lateral Displacement,DLD)采用微柱阵列对微观颗粒进行分选,由于其清洁、简便和可连续分离等优点,在微流控分选技术中占据重要位置[2]。目前,国内外对DLD已经开展了比较广泛的研究工作,然而关于流体和颗粒在芯片微通道中的具体运动情况,仍需深入研究。
目前关于DLD的研究主要集中于微柱形状、排列、粒子类型和边界的影响等方面。早期的DLD装置多采用圆形微柱阵列,近期有学者研究了多边形、流线形[3]甚至“工”字形[4]等微柱阵列的粒子分选特点。传统DLD中的微柱多采用规则的斜向阵列,也有研究人员采用不规则排布[5],达到特别的粒子分选目标。在实际使用中,DLD微柱阵列封装于微流控芯片之中,流道边界的影响需要加以考虑并适合处理[6],以提升分离效果。关于粒子类型,除传统的刚性粒子外,近来有不少研究关注细胞和病毒等生物粒子的分离[7]。由于生物粒子柔性大、可变形和易受损伤等特点,使其分离过程中存在一些独特的现象,有学者专门对此进行了设计[8],保证分离的效率和生物使用性。
确定性横向迁移装置的单元流道尺寸微小,流体速度相对较低,早期有学者根据层流思想,提出了其中的粒子分离理论[9]。然而该理论并未考虑粒子与流体之间的相互作用(多相流),也忽略了边界的影响,可能使理论预测结果出现较大偏差。针对这一问题,随后研究人员根据实验结果对分离理论进行了修正,提出了多种经验模型[10,11]。另一方面,则有学者利用数值仿真技术对DLD的分离机制进行了深入研究。普遍的做法是采用有限单元法或有限体积法,对DLD微柱阵列之间的流体动力学进行计算[7,12]。为探讨粒子与流体的相互作用,Quek等人采用浸入边界法研究变形粒子在DLD中的分离情况[13]。Krueger等则采用浸入边界-格子玻尔兹曼法,研究了变形红细胞在DLD中的运动[14];国内韦建辉等采用类似方法,对变形粒子在圆形、多边形及“工”字形微柱中的运动进行了分析[15]。喻文广等采用直接数值模拟方法对DLD中刚性颗粒的运动进行了计算[16]。数值方法对DLD中流体行为的研究取得了很好的研究成果,不过目前的计算模型多为二维模型,很少考虑芯片顶底边界的影响。关于粒子与流体之间的相互作用,也仍需要继续深入探讨。
格子玻尔兹曼法(Lattice Boltzmann Method,LBM),从介观层面上描述流体状态,在计算上基于粒子描述,特别适合处理多相微流体和复杂边界等问题[17]。本文将采用三维格子玻尔兹曼方法对DLD装置中的微流体和粒子运动进行分析计算,分析不同形状和排列的微柱间的流体运动,研究边界对流场的影响,探讨粒子分离和阻塞等的详细机理。
1 计算模型
1.1 确定性横向迁移基本原理
确定性横向迁移的基本原理如图1所示,分选装置由规则排列的微柱组成,每列微柱与前一列稍微错开,形成斜向排布的阵列。假定阵列的周期为N,微柱间距为λ,则阵列的倾斜度为ε=1/N,相邻列的横向偏移量为ε λ。流体在微柱间流动时,自然形成倾斜的主流道和横向的分流道。考察纵向的流动,由于微柱的“栅栏”效果,流体被分成N条具有相同流量的流束,其宽度为RC。当粒子尺寸显著大于RC时,微柱会连续将其推向相邻的流束,从而使粒子沿倾斜的主流道运动,称为“L”形轨迹。而当粒子尺寸小于RC时,将始终保持在初始流束内,呈现绕微柱而过的“Z”字形轨迹,其总体沿纵向运动。由此,粒子的运动轨迹按临界半径RC区分,可实现不同尺寸粒子的分离[9]。在实际使用中,可以将具有不同临界半径的微柱阵列进行组合,实现更多类别的粒子分离。
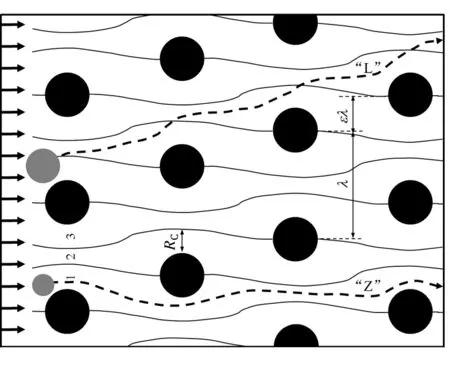
图1 确定性横向迁移的粒子分离原理(以周期N=3示例)
1.2 格子玻尔兹曼模型
格子玻尔兹曼方法(LBM)根据流体微观分布函数的变化,求解流体动力学问题。模型中将将流体离散为一系列的微团,微团以特定方式在规则的格子上碰撞和迁移,如图2所示,对所有格点上的微团运动进行统计,便可得出流体的宏观运动状态。微团的碰撞运动可根据微观分布函数的变化进行描述[18],如下式:

式中: fi表示微团i的微观分布函数;x表示格子上的格点;c表示流体微团的离散速度集合;Δt表示离散时间步长;Ω表示碰撞矩阵; feq表示平衡态分布函数。
碰撞方程可在动量空间中,采用碰撞和迁移两个基本步骤进行数值求解。

图2 格子玻尔兹曼法计算原理
由基本原理可知,LBM是的一种基于拉格朗日粒子描述的计算方法,特别适合多相流动和复杂界面流动的模拟。在LBM的计算模型中,格子的安排有多种方式,本文进行DLD中多相微流动的三维计算,因此选择了三维的D3Q27格子,每个微团可以向邻近的27个格子进行迁移,具有很高的自由度。
关于DLD中固相粒子运动的计算,本文采用的是离散相(Discrete Phase Model,DPM)方法,粒子表示为离散的小球,以拉格朗日方法追踪轨迹,可以对粒子的密度、半径、质量、与边界的碰撞方式等参数进行定义。粒子运动方程如下:

式中:up、 ρp,u和 ρ分别为粒子的运动速度、密度和流体的速度与密度;g为重力;FD为曳力,与粒子直径、流体粘度和雷诺数等参数有关;FA为外力。
1.3 仿真模型及参数
确定性横向迁移的仿真计算模型如图3所示,高度方向(Z轴)与横向(Y轴)两端设为固定边界,横向(X轴)入口设置流速边界条件,速度0.1 m/s ~0.5m/s变化。出口设为压力出口,表压为0。对两种形状的微柱阵列进行了对比计算:“圆柱形”和“鹅蛋形”微柱,其几何外形见图4。圆形微柱的主要参数为:直径50μm,主流道宽度a1=25μm,副流道宽度b1=25μm,阵列周期:N=19;“鹅蛋形”微柱的主要参数:短轴×长轴17×24μm,主流道宽度 a2=32μm,副流道宽度b2=15μm,阵列周期:N=59。微柱高度均为50μm,其他参数详见文献[7][19],选择这组参数方便与文献中的实验数据进行对比,计算流域包含一个完整的微柱阵列周期。
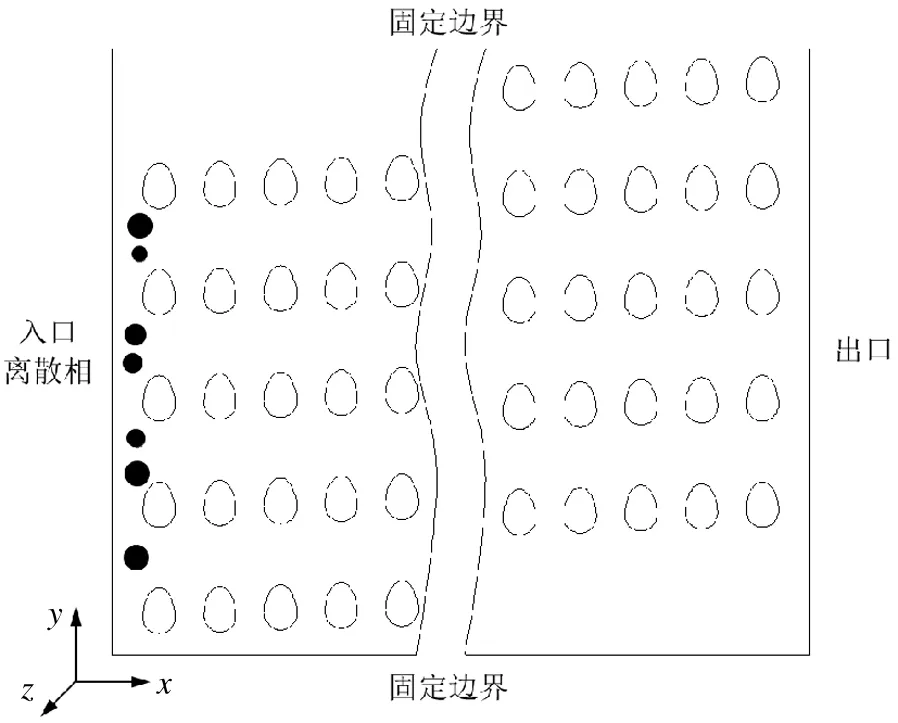
图3 DLD的仿真计算模型

图4 微柱的几何形状及阵列结构
采用均匀格子玻尔兹曼网格,单元的尺寸为2μm,时间步长采用自动调节模式,courant数设置为0.001,采用多松驰方法进行碰撞计算。初步计算表明,采用这些参数,可使稳定性参数维持在1以下,计算结果稳定可靠。临界偏转半径理论值近似为RC~ε a,固相粒子的半径以此为基准,在0.25ε a~4ε a的范围内变化,以精确界定真实临界偏转半径。基础流体设定为液体水,密度为1 000 kg/m3,粘度为0.001Pa·s,每次在微柱阵列入口处释放不同半径的固相粒子,其中固相粒子密度为1 050 kg/m3。
2 仿真结果及讨论
2.1 微柱间的流场分布
对DLD装置中的流场分布进行了分析,圆形微柱间的局部典型流场如图5所示,鹅蛋形微柱的结果类似。从图5(a)水平方向的流场可以看出流体在主流道中的流速最快,粒子将主要沿主流道运动。而副流道中的流速相对较低,而且总体沿横向方向。粒子进行横向迁移,走“Z”形轨迹,必须通过副流道。由于边界的存在,边界附近的微柱后方出现了涡流,有可能使流入其中的粒子发生阻塞。从图5(b)高度方向的流场看到,沿流道的顶边和底边也存在低流速区。粒子主要在中部高流速区运动,少数进入边界附近的粒子有可能发生阻塞。从三维仿真的结果得出结论,不仅是两侧边界,还有顶底边界,都可能对DLD的粒子收集率产生影响。为提高收集率,在实际芯片设计中,可以在两侧边界处开设辅助流道或者增加柱列的总宽度;而为降低顶底边界的影响,可以适当提高微柱的高度,增加有效工作区。

图5 圆形微柱DLD装置中的典型流场(入流速度u=0.5m/s)
相邻两个微柱之间的流场直接决定了粒子的偏转情况,本文对圆形和鹅蛋形相邻微柱间的流速进行了对比,结果如图6所示。速度与坐标都经过了规整化处理,u=u/umax,y=y/w,w为微柱阵列总宽。可以看到,当采用圆形柱列时,两侧边界对流场均匀性的影响更为显著,边界附近微柱间的流速相比中心流速降低率达到15.2%。两鹅蛋形柱列,由于其定向导流作用,流场更加均匀,边界流速降低率低于1%。此外,鹅蛋形微柱间的流场并非对称分布,而是向大端方向倾斜,从而使粒子能更顺利地通过微柱间的流道和副流道,起到减少堵塞的作用。本文的仿真结果证实了非圆微柱对改善DLD阻塞情况的作用,与文献[20]的结论相符。更重要的是,首次揭示鹅蛋形(或三角形,通常鹅蛋形微柱可认为是带有过渡圆弧的三角形微柱,在实际加工中由于锐边加工的困难,实际制备的三角形微柱最终都类似于蛋形)对改善流场的均匀性具有显著效果,可以提高DLD的有效工作区,对DLD装置的优化设计具有指导作用。

图6 圆形和鹅蛋形微柱间流速的对比
2.2 临界偏转半径
对粒子在圆形和鹅蛋形微柱阵列中的粒子运动轨迹进行追踪,典型结果如图7、8所示。由理论公式估算,圆形和鹅蛋形微柱阵列中的粒子偏转半径分别约为3μm和2μm,因此计算了半径在1~6μm (间隔0.5μm)之间的粒子的运动情况,分析了不同尺寸粒子的运动轨迹。在圆形DLD中,发现当粒子半径小于3.5μm时,运动轨迹为Z模式,而粒径大于4μm的粒子运动模式为L模式。为更精确界定临界偏转半径RC,进一步细分粒子直径,发现RC约为3.5μm。
而在鹅蛋形微柱阵列中,也计算了半径在1~6μm(间隔0.5μm)之间的粒子的运动情况,发现当粒子半径小于2μm时,运动轨迹为Z模式,而粒径大于2.5μm时,粒子运动模式为L模式。进一步细分发现RC约为2.4μm。本文数值计算的临界偏转半径与文献[7][19]中的研究结果相符。
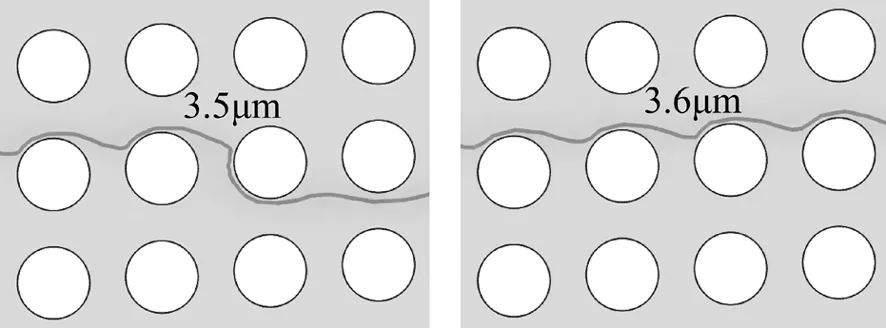
图7 圆柱形微柱阵列粒子运动轨迹

图8 鹅蛋形微柱阵列粒子运动轨迹
为对比圆形与鹅蛋形微柱阵列的粒子通过性,计算了各自的主流道宽度-临界偏转半径比率 γ = a / Rc。圆形阵列 γ = 7.1,而鹅蛋形阵列 γ = 13.3,接近为圆形阵列的2倍。以上结果表明:为达到相同的偏转效果,鹅蛋形阵列允许采用更宽的主流道,而宽流道意味着更好的粒子通过性,可显著改善粒子阻塞现象。
本文还研究了速度对临界偏转半径的影响,发现不同速度下的临界偏转半径几乎没有变化。其原因是由于微流道的特征尺寸很小(10-6m量级),在通常工作流速下(10-1m/s量级),由雷诺数计算公式可知其雷诺数为10-1量级,远小于2 300,故其流动呈层流状态,流场特性没有随着速度变化发生明显变化,因此临界偏转半径不变。
3 结论
确定性横向迁移(DLD)是一种应用广泛的粒子分选技术,本文采用三维格子玻尔兹曼法,对DLD中的流场特性和粒子临界偏转半径进行了研究。对比了圆柱形和鹅蛋形DLD中的流场特性,仿真发现非圆微柱能改善DLD的阻塞,与之前文献中的结论相符。相较于圆形阵列,鹅蛋形阵列在改善流场的均匀性方面具有显著效果,可以提高DLD的有效工作区。仿真还计算了粒子的临界偏转半径,计算结果与前人的实验结果一致。这些结论对DLD装置的优化设计具有指导作用。
