最值问题的错例剖析

（安庆二中南区 安徽安庆 246003）

最值问题是中学数学的热点问题，其解法繁多且灵活多变，而且涉及的知识面颇宽，求解时稍有不慎，极易出现因思路紊乱而导致错解、误解的现象，而且某些错误又较为隐蔽，不易被人们所察觉。下面分类解析一些常见的错误题解，通过展示错解，剖析错因，给出正确解答，以达辨别正误，暴露错因，提高解题能力的目的。

一、消元时忽视条件的限制致误。

解二元条件最值问题，常通过消元减少变量，但在消元过程中要注意各变量之间相互制约关系。

二、换元时忽视变量的范围致误

换元前后的变量之间实际上是自变量与因变量的关系，确定换元后的表达式中变量范围时充分考虑换元前变量范围的限制。

三、忽视定义域致误

错解1：将原式右边的x移到左边，两边平方后整理，得x2−(2y+1)x+(1+y2)=0为使关于x的一元二次方程有实数解，必须要有∆=[−(2y+1) ]2−4(1+y2)≥0，

四、忽视重要不等式中等号成立的条件致误

例4 已知x为锐角，求函数y=sinxcos2x的最小值。

五、利用均值不等式解题忽视成立的条件

均值不等式中求最值是一种常用的方法，但要注意“正”、“定”、“等”是均值不等式成立的前提。解题时需考察式子是否具备均值不等式成立的条件，进行适当的拆、添、配、凑等策略进行求解。

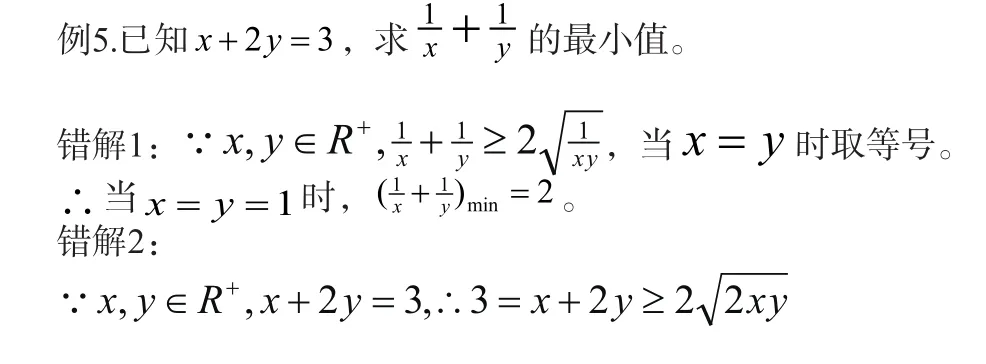
六、忽视值域致误

分析：此解法看似正确。其实不然，将原来函数平方后y的取值范围随之扩大。

正解：

七、方程法求函数值域时忽视检验

错解：

分析：函数（1）的定义域为x≠1，函数（2）的定义域为x∈R，所以（1）与（2）并非同一函数，当然（2）的值域也不一定是（1）的值域，而当x=1时，方程（2）中y=3，但当y=3时，方程（1）的解恰为x=1，而x=1并非（1）的定义域内的值，故（1）⇒（2）变形中值域扩大了。

正解：

从以上分析可知要去掉y=3.所以y的值域为y∈ ( − ∞,3)U(3,+ ∞)。

八、滥用函数值域的对称性而忽视表达式的结构特征。

一般函数的值域都不具备对称性，而要根据表达的结构特征，分别确定其上限和下限，不能滥用值域的对称性解题。因此，可通过类比，数形结合，特值否定来消除“值域对称”的影响。

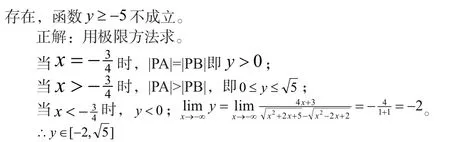
九、盲目利用判别式解题而函数问题的慎密讨论。

十、忽视隐含条件致误

综上所述，错解的原因是多方面的，以上仅归纳十种类型。一般，造成错解的原因是解题者对某些概念混淆不清，公式、定理掌握不牢，理解不透。基本的方法、技能不能正确、灵活运用所致，同时思维不慎密，缺乏防错意识也是一个原因。所以只有保持头脑清醒，认真分析，联系自己所学知识，才能起到既提高解题速度又保证解题质量的效果。