关于洛必达法则的若干思考

（石河子大学理学院数学系 新疆石河子市 832001）

引言

函数极限是高等数学中一部分重要的内容。若当自变量x→a（a 为常数或∞）时，两个函数f(x)，g(x)都趋于零或者无穷，这时极限可能存在，也可能不存在，这时称这种极限为未定式极限，并分别记为或。 我们通常会使用洛必达法则去解决这一类极限。类似地，在解决0·∞、∞−∞、00、1∞、∞0这些类型的未定式极限时，也可先将其转化成或型未定式，再求其极限.当然，在使用洛必达法则求此类极限时有一定的使用条件，并且洛必达法则并不是解决上述类型的极限的最简便的方法。本文论述了运用洛必达法则解决型未定式极限时遇见的若干问题，并且简述了复变函数中解析函数求极限时洛必达法则的使用条件。[1]

1．洛必达法则

定理1（柯西（Cauchy）中值定理）：函数f(x)，g(x)满足：①在闭区间[a,b]上连续；②在开区间(a,b)内可导；③对任意x∈(a,b)且g'(x)≠0，则至少有一点ξ∈(a,b)[2]

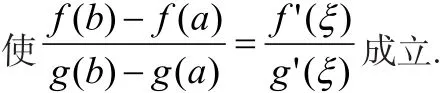
定理2（洛必达法则）：函数f(x)，g(x)在点x0的某个邻域内有定义，满足：[3]

①当x→a 时，函数f(x)，g(x)都趋于零；

②在x0的该邻域内，其导数f'(x)，g'(x)都存在且g'(x)≠0；

证明：洛必达法则成立时，我们补充定义f(x0)=g(x0)=0，这样就使得f 与g 在x0点处连续。任取x∈U0(x0)，在区间[x0,x]（或[x, x0]）上，满足柯西中值定理条件，

3．有些未定式直接使用洛必达法则求极限会比较麻烦，可以综合求极限的其他方法，如等价无穷小代换、重要极限、极限运算法则等尽可能地先简化算式。

解：原式若直接用洛必达法则解此题比较麻烦，可先利用等价无穷小简化，再求解。

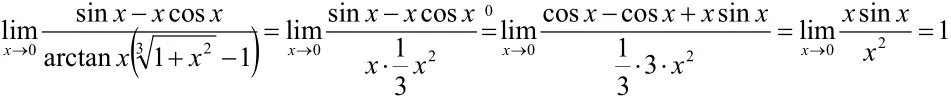
4．洛必达法则仍可以解决复函数极限问题

定理3：若f(z)及g(z)在z0解析，

实际上，若函数在z0点处解析，有该函数在z0的领域内处处可导，

即：

下面从幂级数角度来证明.证明：由函数f(z)及g(z)均在z0点解析，则在z0点的某个领域内，函数f(z)及g(z)可展为：

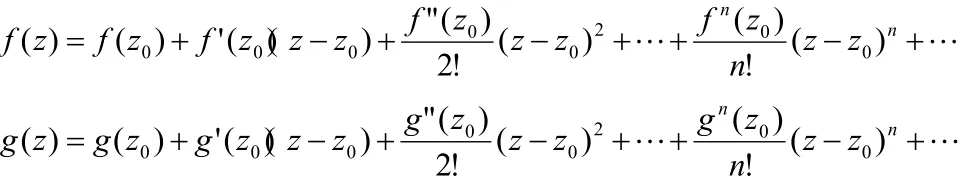
即

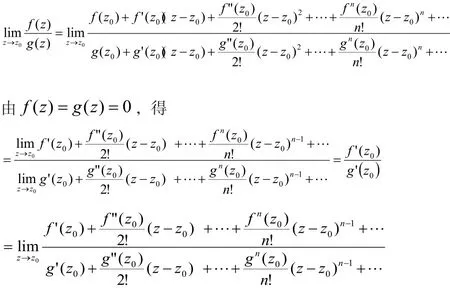
证毕

结语

1．在使用洛必达法则求未定式极限问题时，因当注意洛必达法则的使用条件，结合具体题型，选择合适的方法。