常见离散型概率分布及其联系

（北京师范大学附属实验中学 北京 100032）

一、常见离散型概率分布及其数学期望

本小节主要介绍一些常见的古典概率模型，并简单计算出这些常见离散型随机变量的数学期望。[1]

1．伯努利分布

假设在一次独立重复试验中（伯努利试验），事件发生的概率p,不发生的概率为q=1-p,也就是说P(A)=p,P(`A)=1-p 我们定义随机变量1为，[2]

我们称1服从伯努利分布,记作

则伯努利分布的概率分布为，

伯努利分布的数学期望为，

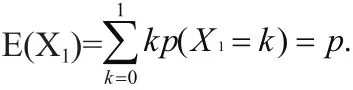
2．二项分布

二项分布是伯努利分布的推广，在次伯努利试验中，我们定义随机变量为事件发生的次数，则称随机变量2服从二项分布,记作

随机变量的概率分布为，

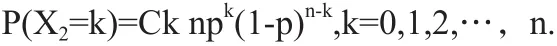
二项分布的数学期望为，

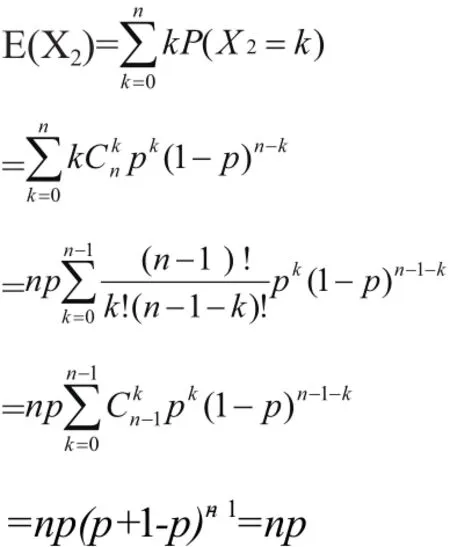
3．几何分布

假设某人射击每次中靶的概率为, 并且每次射击互不影响，（相当于次伯努利试验）,若将射击进行到有一次中靶为止，我们定义随机变量3为总共射击的次数。我们称随机变量3服从几何分布,记作

那么，几何分布的概率分布为，

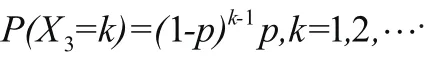
几何分布的数学期望为，

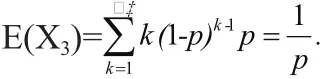
4．帕斯卡分布

帕斯卡分布是几何分布的推广，假设某人射击每次中靶的概率为, 并且每次射击互不影响，若将射击进行到有（这里为正整数）次中靶为止，我们定于随机变量4为总共射击的次数。我们称随机变量4服从帕斯卡分布，记作

帕斯卡分布的概率分布为，

帕斯卡分布的数学期望为，

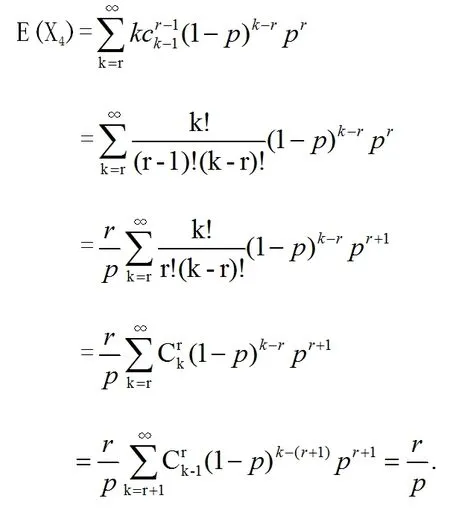
5．超几何分布

假定在件产品中有件次品，其余产品为正品，在件产品中随机抽取件产品，记5为次品件数，则称随机变量5服从超几何分布，记作

超几何分布的概率分布:

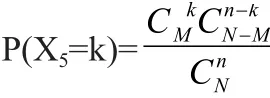
二、离散型随机变量之间的联系

超几何分布与二项分布在极限意义下是统一的，即超几何分布在极限意义下（总产品数足够多时）逼近二项分布，在下文我们给出这个结论。

假设是一个服从超几何分布的随机变量，即其概率分布为：

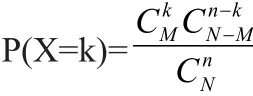
在这里我们假设，M=Np,其中为介于到之间的常数。

将式P(X=k)化简可以得到，

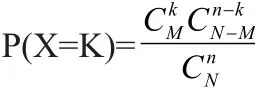
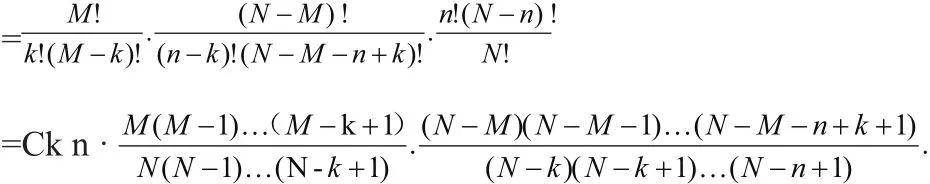
取极限我们可以得到，

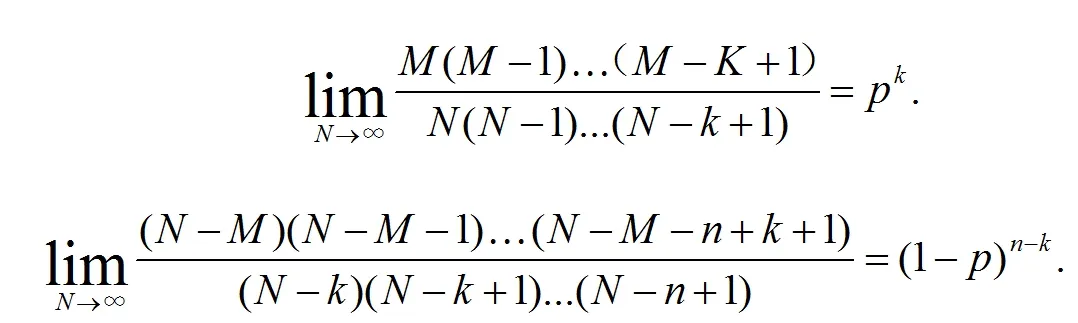
因此我们有，

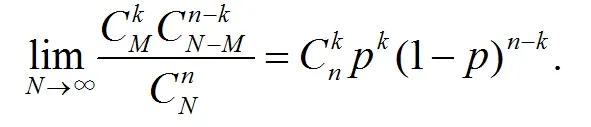
故当足够大时，超几何分布逼近了二项分布。

从超几何分布和二项分布所代表的实际意义来看，我们假设次品总数占产品总数的比例一定，也就是说次品的概率是确定的，并且当产品总数足够多，抽取的产品数比较少时，我们进行有放回的抽取产品和无放回的抽取产品，抽到次品的概率几乎是不变的，也就是说从所有产品抽取件产品出来，可以看作是一件一件抽取出来的，即可以看作是次独立重复试验，这样超几何分布在极限意义下（总产品数足够多时）逼近二项分布。

结语

本文所介绍的伯努利分布、二项分布、几何分布和帕斯卡分布都是和伯努利试验相关的概率分布，但超几何分布并非和伯努利试验相关的概率分布，主要系从超几何分布实际意义来看，抽取产品是无放回的，但当总产品数足够多时，无放回的抽取产品可以看为伯努利试验，这样超几何分布也可以看作是和伯努利试验相关的概率分布。