山区斜坡型桥梁墩梁固结研究

王建金

(贵州省交通规划勘察设计研究院股份有限公司 贵阳 550081)

山区地形变化复杂,高差大。在山区公路桥梁设计中，采用标准化、施工便利的小跨径预制拼装结构对缩短工期、降低工程造价有着重要意义。在高差较大的山区，桥梁高墩普遍存在[1]。墩梁固结将桥梁中的1个或几个桥墩与主梁固结起来，形成刚构体系。利用桥墩自身的柔性适应上部结构的变形，利用刚构抵抗车辆制动力。墩梁固结后，高墩的稳定性提高，因而墩身可以采用较经济、施工工艺相对简单的外形, 施工安全度相对较高。墩梁固结使桥墩受力状态发生较大变化，有必要对墩梁固结前后桥墩的受力状态进行详细的计算分析。

山区地形复杂多变，本文着重研究桥位地面呈“斜坡形”的桥梁墩梁固结前后桥墩的受力特性。结合工程实例建立斜坡形桥梁的midas有限元模型，从桥墩受力的角度，对桥梁墩梁固结前后桥墩的受力状态进行分析，得到中小跨径桥梁墩梁固结前后的受力特性变化规律。

贵州山区某在建斜坡形桥梁，设计车速为80 km/h，2车道，荷载等级为公路-I级。桥梁上部采用5×30 m预制T梁结构，桥墩采用双圆柱墩或实心墩，桥墩从左至右进行编号，分别为1，2，3，4号桥墩。所有桥墩均采用圆柱墩时，各桥墩的墩高及墩柱截面尺寸为：1号桥墩，双圆柱墩，H=40 m，D=2.0 m；2号桥墩，双圆柱墩，H=30 m，D=2.0 m；3号桥墩：双圆柱墩，H=20 m，D=1.8 m；4号桥墩，双圆柱墩，H=10 m，D=1.6 m。墩高最高的1号桥墩采用实心墩，其余桥墩采用圆柱墩时，各桥墩的墩高及墩柱截面尺寸为：1号桥墩，实心墩，H=40 m，尺寸为6.5 m×2.4 m；2号桥墩，双圆柱墩，H=30 m，D=2.0 m；3号桥墩，双圆柱墩，H=20 m，D=1.8 m；4号桥墩，双圆柱墩，H=10 m，D=1.6 m。下部结构一般构造见图1、2。

图1 T梁圆柱墩一般构造图(单位：cm)

图2 T梁实心墩一般构造图(单位：cm)

1 计算体系的拟定及力学模型的建立

1.1 荷载工况

桥梁墩台将上部结构自重及其所受的各种荷载传递到基础，桥墩除了承受来自桥梁自身重量的竖直向荷载外，还承受了通过上部结构传递的或直接承受的水平向荷载，最终使桥墩处于偏心受压状态。桥梁墩台通过支座与桥梁上部结构连接成整体，桥墩设计内力计算时，建立全桥模型，通过有限元计算软件等方法得到桥墩的内力。

桥梁计算时应考虑的荷载工况包括：

1) 桥梁结构恒载。包括自重和二期荷载。

2) 汽车荷载。利用有限元计算软件miads建立桥梁模型，定义车道荷载，对结构进行受力分析。

3) 汽车制动力。汽车制动力对桥墩所受水平力有较大贡献，不可忽略，不小于汽车荷载在加载长度上总重力的10%。

4) 温度荷载。包括均匀温度荷载、梯度温度荷载，其中均匀温度荷载对桥墩的水平受力有较大影响，梯度温度荷载对桥墩受力影响较小。非线性温度梯度按JTG D60-2015 《公路桥涵设计通用规范》[2]规定执行。

5) 支座沉降。，每个桥墩支座设为同一支座沉降组，沉降量按0.005 m考虑。

6) 纵、横向风力。桥墩高度较大时，风荷载对桥墩的受力有较大影响，不能忽略。

7) 收缩徐变。按成桥10年收缩徐变考虑。

1.2 力学模型的建立与简化

1.2.1内力计算

根据上述的墩高组合，分别建立2个模型进行静力计算分析。

模型一，所有桥墩均采用圆柱墩。

模型二，墩高最高的1号桥墩采用实心墩，其余桥墩采用圆柱墩。

有限元模型中，桥墩与主梁采用板式橡胶支座连接，桥墩底面采用刚性支承。建立的midas模型见图3、图4。添加前述的荷载工况，计算得到不考虑偏心距增大系数的桥墩截面弯矩Md和轴力Nd。

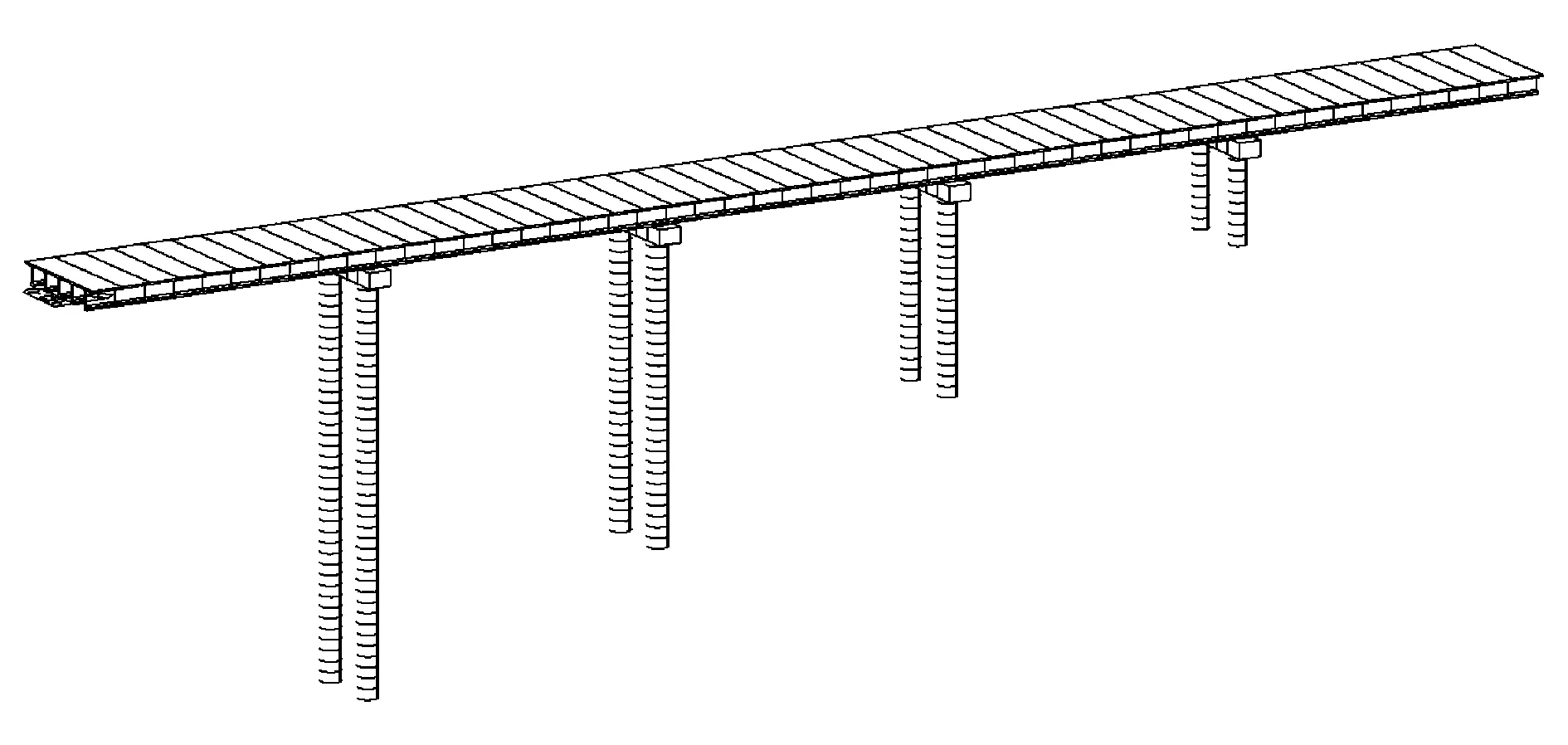
图3 所有桥墩均采用圆柱墩时的midas模型(模型一)

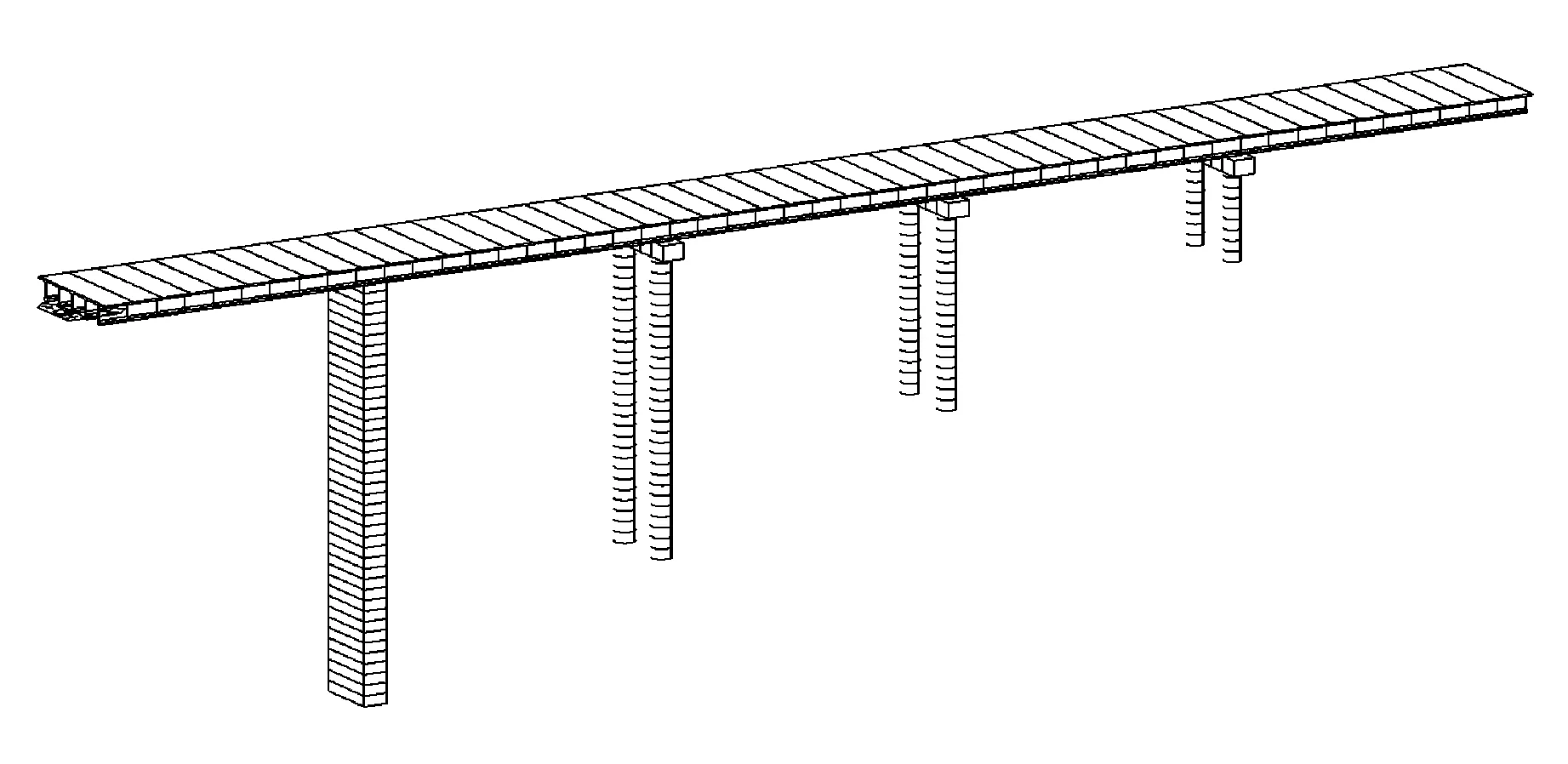
图4 1号桥墩采用实心矩形墩，其余桥墩采用圆柱墩时的miads模型(模型二)

1.2.2等效刚度的计算

桥墩承载力的计算，需要根据桥墩边界条件确定其计算长度。墩顶边界条件等效为刚度水平的弹性支承。如图5所示。

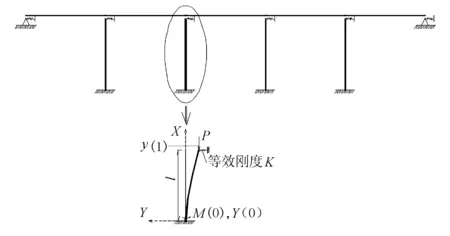
图5 墩柱墩顶等效刚度计算简图

等效刚度在有限元模型中的求解过程如下：桥墩顶节点施加单位1的位移，通过静力计算分析得到该节点处的假想支反力，该支反力即为整个全桥结构在该点处总的水平抗推刚度。用桥墩顶的总水平抗推刚度减去桥墩在自由状态下作为悬臂梁的水平抗推刚度，即可得到上部结构对该桥墩顶的等效水平支承刚度。

墩柱墩顶悬臂抗推刚度计算公式如下

式中：l为墩柱高度，m；I为墩柱截面抗弯惯性矩，m4；E为墩柱材料抗压弹性模量，Pa。

利用得到的等效水平抗推刚度，根据山区桥梁墩柱长度系数计算方法[3-4]可计算得到墩柱的计算长度系数μ。

1.2.3偏心距增大系数及控制弯矩的求解

根据JTG D62-2004 《公路钢筋混凝土及预应力混凝土桥涵设计规范》[5]计算偏心距的增大系数η。

式中：l为墩高；h为截面高度；h0为截面有效高度；e0为轴向力偏心距；ζ1，ζ2分别为系数。将桥墩截面弯矩Md和轴力Nd，计算长度系数μ代入上式可计算得到增大系数η值。控制弯矩即为ηMd。

2 计算结果分析

2.1 模型一

按桥墩高度从高到低对桥墩进行编号，分别为1～6号。根据墩梁固结的情况，分6种情形进行计算：情形1，墩梁不固结；情形2，固结1号墩；情形3，固结2号墩；情形4，固结3号墩；情形5，固结4号墩；情形6，固结2，3号墩。对于每种情形，计算各桥墩的长度系数、偏心距增大系数、桥墩的控制轴力和控制弯矩ηMd。进而对每一种情形桥墩的受力特性和优劣进行判断。模型一(桥墩均为圆柱墩)各墩梁固结情形下桥墩控制弯矩的变化见图6。

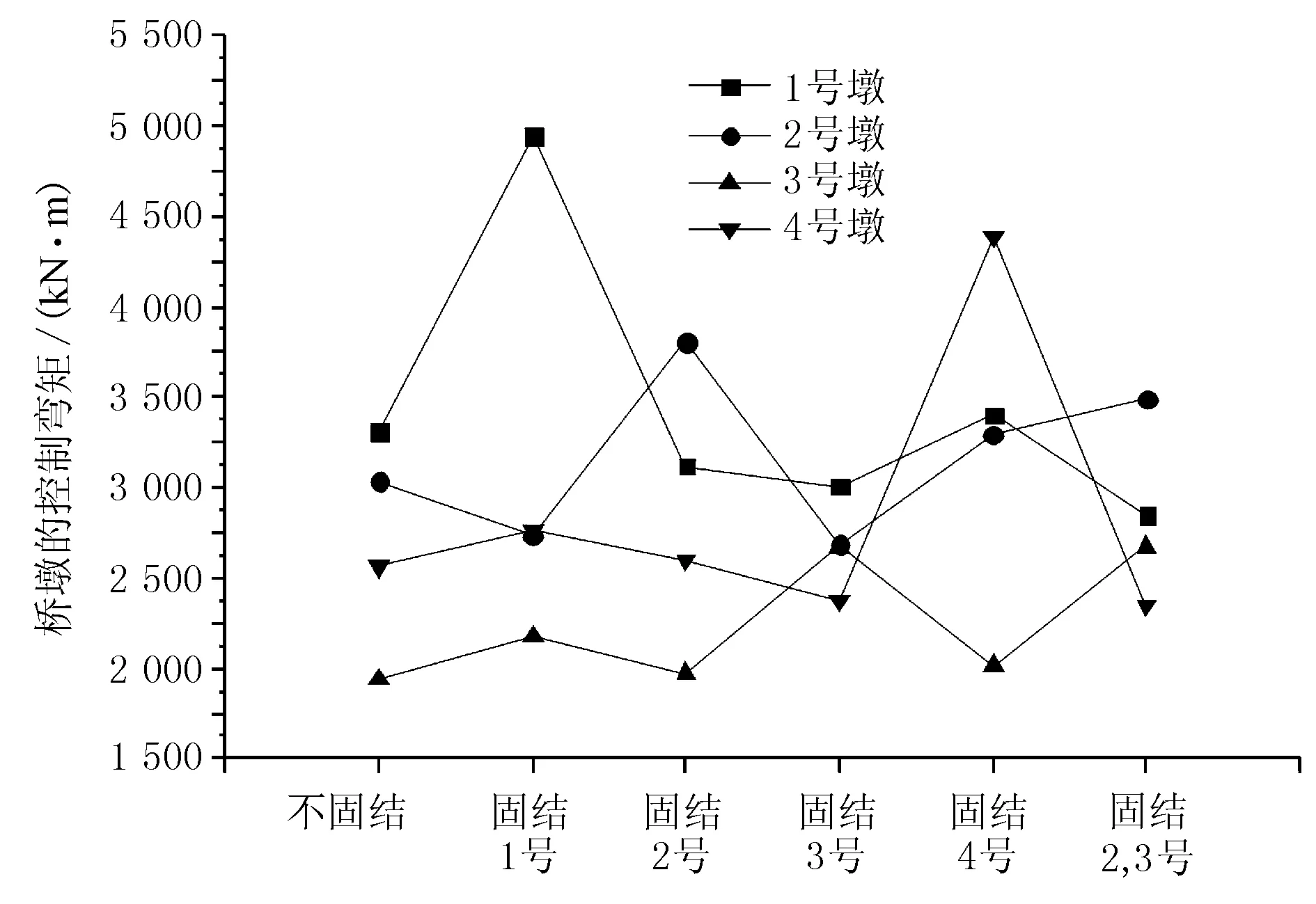
图6 模型一各墩梁固结情形下桥墩控制弯矩图

由图6可见，对于斜坡型墩高，模型一桥墩均为圆柱墩，各桥墩间截面尺寸相差不大，墩梁固结确实能有效地改善桥墩的受力状态。分析计算结果可以得到以下结论。

1) 固结1号墩时，其余桥墩的控制弯矩ηMd无太大变化，1号墩的控制弯矩由3 306.98 kN·m变为4 943.11 kN·m，有较大增加。

2) 固结2号墩时，桥墩的控制弯矩ηMd与不固结时相比变化不大。

3) 固结3号墩时，3号墩的控制弯矩有所增大，其余桥墩的弯矩均有一定程度的减小，桥墩弯矩的分布变得均匀，整个桥梁桥墩的受力性能得到改善。由于体系墩梁不固结时，1～4号桥墩中，3号桥墩靠近桥梁中心，温度和收缩徐变引起的内力小，其控制弯矩最小，所以固结3号墩时，控制弯矩增加的数值不至于过大，而且由于3号墩的固结，其他桥墩的控制弯矩均有相应的减小。所以固结3号墩是合理的选择。

4) 固结4号墩时，4号墩控制弯矩有较大增加，其余桥墩控制弯矩变化不大。

综上，当固结3号墩或同时固结2，3号墩时，桥梁体系的受力更为合理。

2.2 模型二

根据墩梁固结的情况，分5种情形进行计算：情形1，墩梁不固结；情形2，固结1号墩；情形3，固结2号墩；情形4，固结3号墩；情形5，固结4号墩。对于每种情形，计算每个桥墩的长度系数、偏心距增大系数、桥墩的控制轴力和控制弯矩ηMd。进而对每一种情形桥墩的受力特性和优劣进行判断。模型二(1号墩为实心墩)各墩梁固结情形下桥墩控制弯矩的变化如图7所示，图中各桥墩的弯矩值为相对于体系不固结时桥墩弯矩值(假定不固结时各桥墩弯矩值为1)。

图7 模型二各墩梁固结情形下桥墩控制弯矩图

由图7可见，对于斜坡型墩高，模型二1号桥墩为矩形实心墩，其余桥墩均为圆柱墩，各桥墩间截面抗弯惯性矩相差较大。分析计算结果可以得到以下结论。

1) 墩梁不固结时，由于1号墩刚度大，且墩柱高，所以分配的控制弯矩远远大于其他桥墩，1号桥墩受力状态是整个桥墩体系受力控制的关键。

2) 固结1号墩时， 1号墩的长度系数由1.984变为1.135，偏心距增大系数由3.767变为1.863，控制弯矩降低超过10%。2号墩的控制弯矩也有较大程度的降低，远离1号墩的3，4号墩的控制弯矩有较大程度的增加，因为3，4号墩控制弯矩增加后的弯矩数值均较小，所以从全局来看，固结1号墩合理。

3) 固结2号墩时，桥墩的控制弯矩ηMd与不固结时相比变化不大，不能体现出墩梁固结的优势。

4) 固结3号墩时，3号墩的控制弯矩有较大增大，其余桥墩的弯矩基本维持不变，墩梁固结后桥墩受力不利。

5) 固结4号墩时，4号墩控制弯矩有较大增加，其余桥墩控制弯矩变化不大。

在斜坡型墩高体系中，当墩高较大的墩采用刚度很大的实心墩时，桥墩将受到很大的控制弯矩作用。该类桥墩将作为桥墩受力计算的控制点。墩梁固结能有效改善桥墩的受力性能，所以对于这种墩高组合体系，应固结对受力状态起控制作用的桥墩。如模型二中的1号实心墩，虽然远离桥梁中心，但是其作为桥梁下部结构计算的控制点，对其进行固结能有效地提升受力性能，优化截面尺寸，所以应予以固结。

综上，当固结1号实心墩时，桥梁体系的受力更为合理。

3 结论

1) 对于斜坡型墩高体系，合理的墩梁固结能有效地改善桥墩的受力状态。

2) 对于各桥墩间截面抗弯惯性矩相差不大的情况，体系墩梁不固结时，靠近桥梁中心的桥墩，其控制弯矩最小，所以固结这类墩时，控制弯矩增加后的数值不至于过大，而其他桥墩的控制弯矩均有相应的减小。

3) 在斜坡型墩高体系中，当墩高较大的墩采用刚度很大的实心墩时，桥墩将受到很大的控制弯矩作用。该类桥墩将作为桥墩受力计算的控制点。

4) 固结桥梁体系中墩高较高、刚度较大的控制墩，能有效地改善桥墩的受力性能，降低墩柱的控制弯矩。