施工硬化阶段半刚性基层干缩应力计算方法
2018-10-11张兴华
张兴华
(广州市市政工程设计研究总院有限公司 广州 510060)
施工硬化阶段,在水平摩阻力作用下(见图1a),半刚性基层均匀失水时,梁截面不仅产生水平轴力N,而且会产生弯矩M(见图1b),而以往计算干缩应力时,往往忽略了梁截面因地基水平摩擦阻力所引起弯矩的影响[1-3]。因此,在进行水泥稳定碎石基层干缩应力计算时,有必要弄清弯矩M的影响。其中:kv为地基反应模量,MPa·m-1;ku为地基水平摩擦阻力系数,MPa·m-1;M(x)为截面弯矩,N·m;V(x)为截面剪力,N;N(x)为截面轴力,N;L为基层长度,m;h为基层厚度,m。
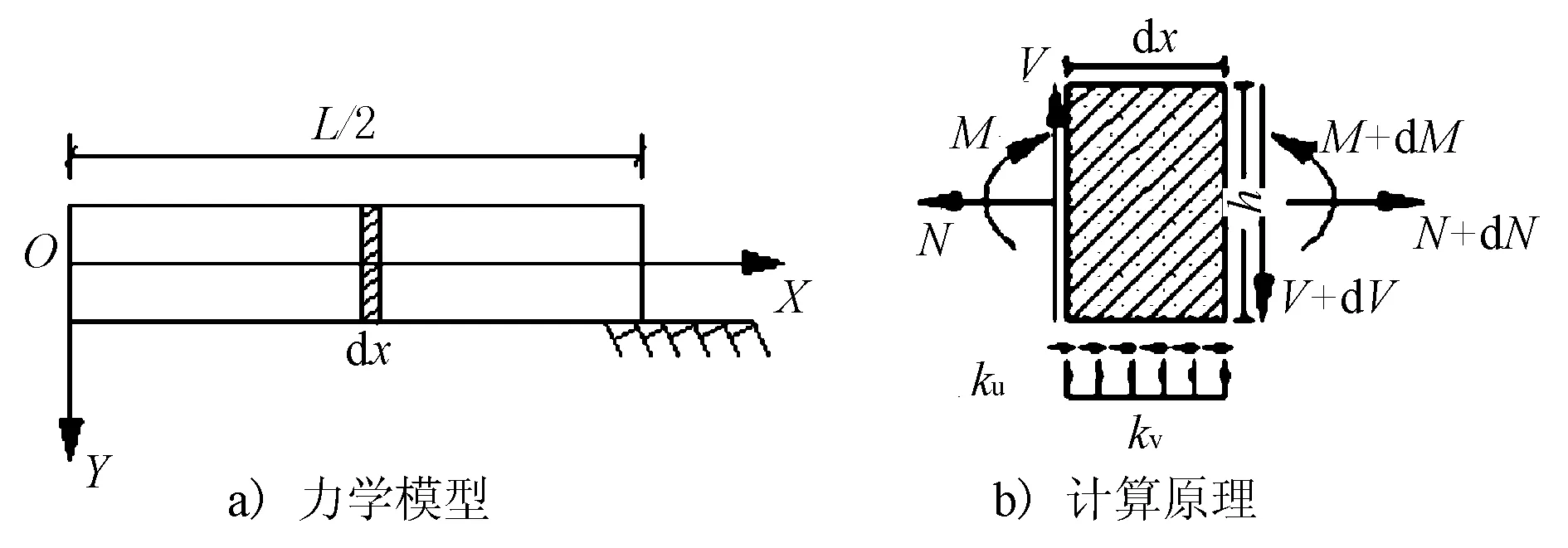
图1 力学模型及计算原理图
1 干缩应力模型
1.1 干缩应力解析解
在水平摩阻力作用下,梁截面微元体的变形假设、微分方程的建立与求解参考文献[4]。
求解过程中微分方程边界条件可等效为如下形式
x=L/2,N(x)=Nm
x=L/2,M(x)=0
(1)
x=L/2,V(x)=0
式中:Nm为虚拟轴力,Nm=EAαdΔm,其中:E为弹性模量,MPa;A为梁截面面积,m2;αd为干缩系数,10-6/%;Δm为含水率的均匀变化量,%。
弯矩引起基层截面的弯拉应力为
(2)
基层截面因含水量均匀变化所引起的干缩应力为
(3)
式中:Wz为弯曲截面系数,对于矩形截面,Wz=Bh3/(12y),m3,其中:B为基层单位宽度,m。
1.2 干缩应力的简化解
当kv趋于无穷大时,w(x),M(x)趋于零,可得湿度均匀变化时基层轴向干缩应力σs(x)和收缩位移u(x)为
(4)
(5)
当x=0时,基层截面平均收缩应力σ(x)取得最大值
(6)
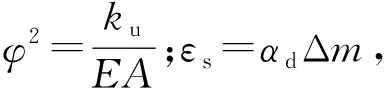
2 解析解弯矩、弯沉分析
2.1 参数取值
水平摩阻系数ku是导致基层产生干缩应力的主要原因,参考文献[5]中建议:当底基层为土基时,ku取60 MPa/m;底基层为石灰土时,ku取60~100 MPa/m;底基层为水泥稳定类材料时,ku取100~600 MPa/m。半刚性基层参数取值见表1。

表1 模型参数
2.2 弯矩变化
当ku取不同值时,图2a)给出了L=50 m、,h=0.25 m,kv=60 MPa/m时,解析解的弯矩变化图;当kv取不同值时,图2b)给出了L=50 m,h=0.25 m,ku=100 MPa/m解析解的弯矩变化图。
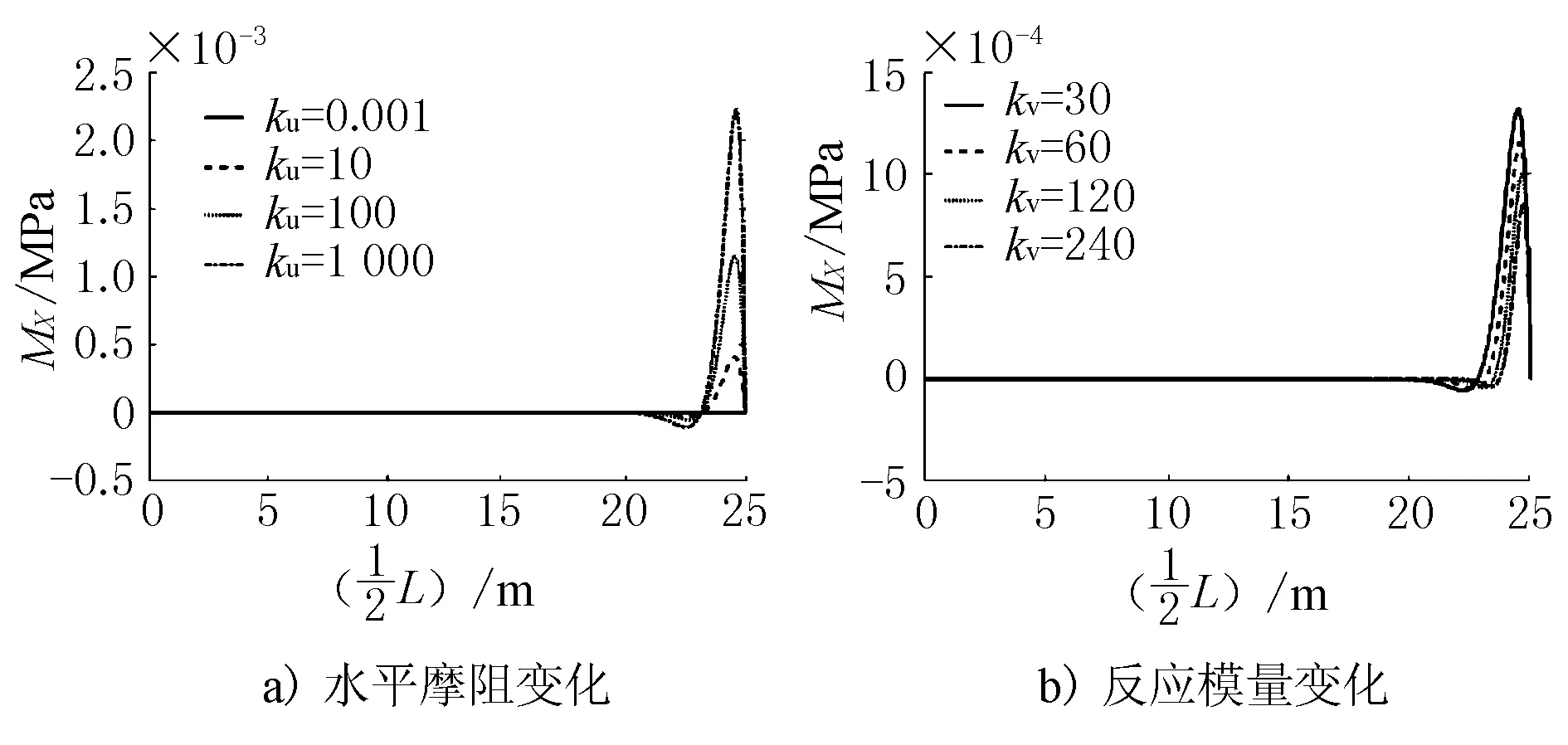
图2 基层弯矩变化曲线
由图2可见,弯矩在基层中部区域基本为0,在接近端部区域先略微降低,而后迅速增大又降低为0。基层最大弯拉应力发生在端部区域的底部,并且弯矩的最大值随着ku的增加而增加、kv的增加而减小。
2.3 弯沉变化
当ku取不同值时,图3a)给出了L=50 m,h=0.25 m,kv=60 MPa/m时,地基梁的弯沉变化曲线图;当kv取不同值时,图3b)给出了L=50 m,h=0.25 m,ku=100 MPa/m时,地基梁的弯沉变化曲线图。
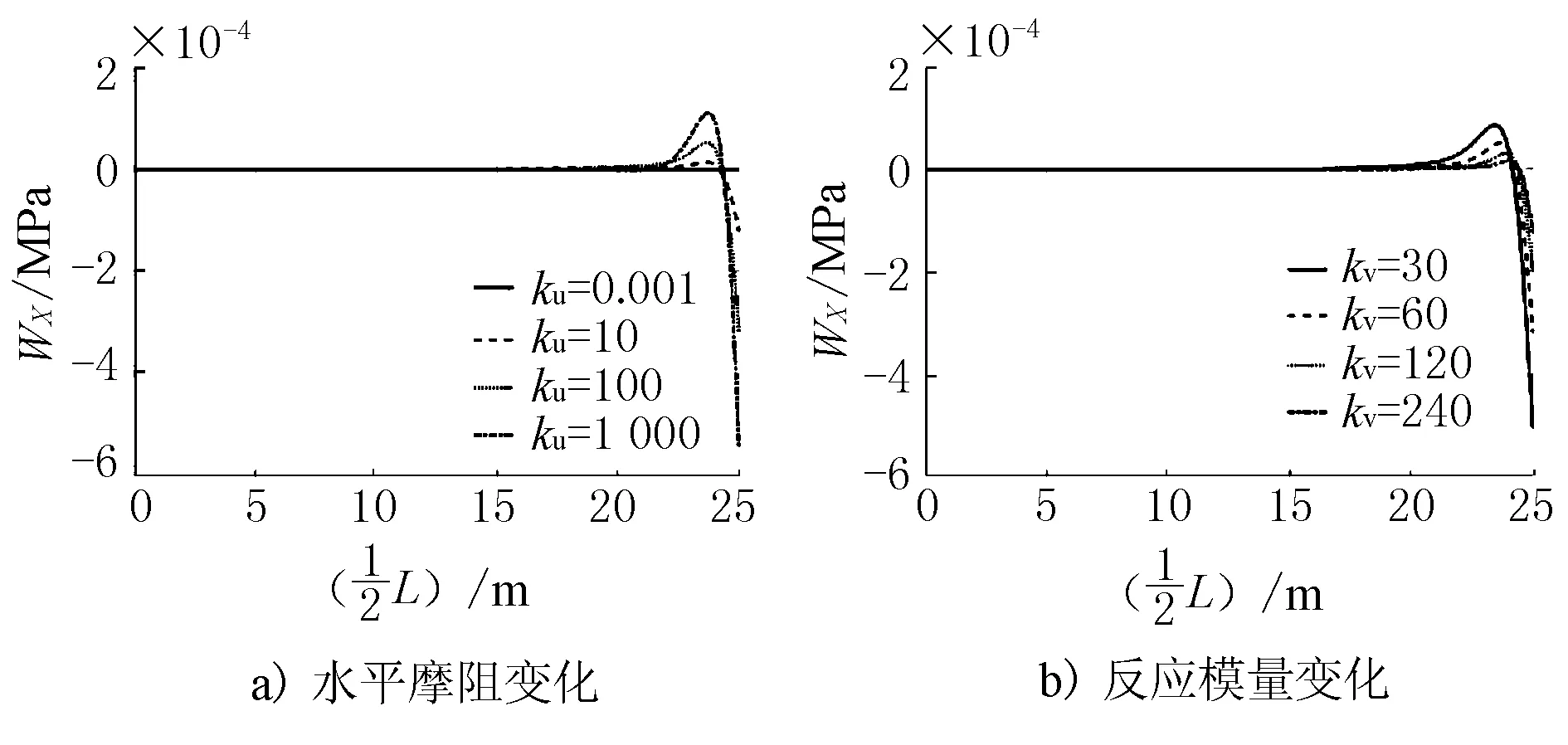
图3 基层弯沉变化曲线
由图3 可见,地基梁的弯沉在基层中部区域基本为0,在接近端部区域迅速增大,曲线出现凸起,而后弯沉降低为0出现反弯现象,并在基层端部达到最大值,其最大值随着ku的增加而增加、kv的增加而减小。
3 解析解、简化解的干缩应力对比分析
图4给出了L=50 m,h=0.25 m,ku=100 MPa/m,kv=60 MPa/m时,解析解对应的基层顶部和底部干缩应力沿长度方向的变化曲线图。

图4 基层顶面、底面干缩应力变化曲线
由图4可见,无论基层的顶面或底面,干缩应力均是在基层中部取得最大值,且基层顶面和底面的干缩应力值基本相同,弯拉应力影响较小。在端部区域,基层顶面会出现局部受压情况,而基层底面则均为受拉状态。与基层中部区域相比,由于基层端部干缩应力较小,因此对基层开裂的影响不大。
图5给出了基层长度L、基层厚度h及水平摩阻系数ku不同时,干缩应力解析解(考虑弯矩作用)和简化解的干缩应力变化曲线(见图4中a)、c)、e))及解析解与简化解比值的变化曲线(见图4中b)、d)、f))。
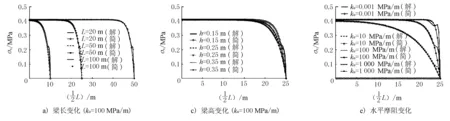
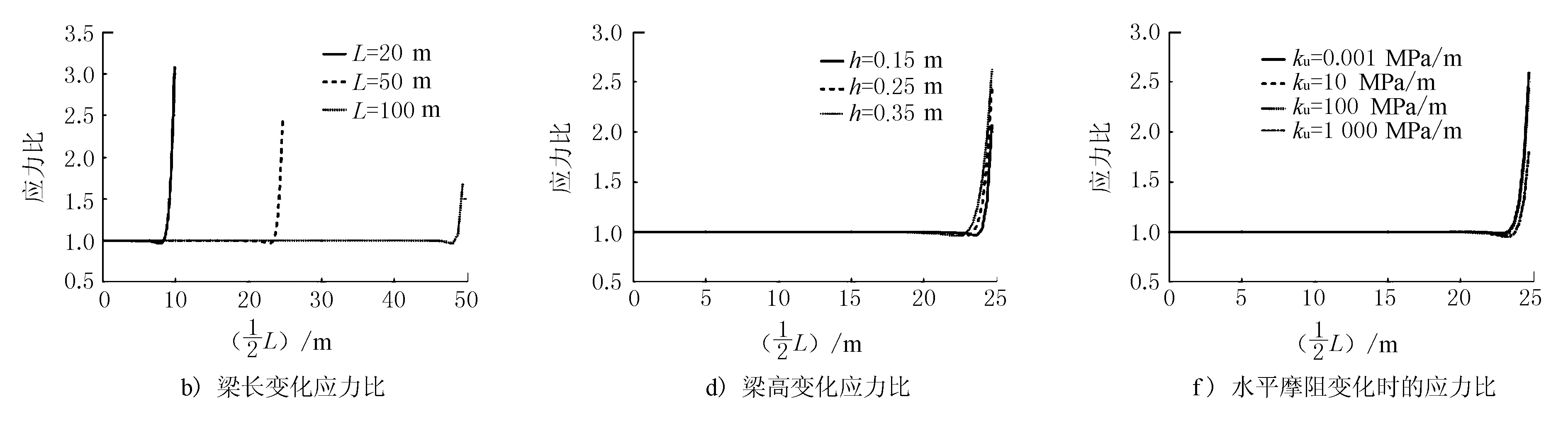
图5 2种模型干缩应力对比曲线图
由图5可见,基层长度L、基层厚度h及水平摩阻系数ku变化时,在基层中间区域2种干缩应力模型所得干缩应力比值较为稳定,均接近1,而在基层端部的干缩应力则有所变化,但因基层端部的干缩应力对基层开裂影响不大,在进行基层开裂计算时可不予以考虑,因此,在计算半刚性基层施工硬化阶段的最大干缩应力时,可采用简化解。
4 结论
1) 水平摩擦阻力作用下,半刚性基层截面弯矩在基层中部区域几乎为0,在接近端部区域先略微降低,而后迅速增大又降低为0。基层最大弯拉应力发生在端部区域的底部,并且弯矩的最大值随着ku的增加而增加、kv的增加而减小。
2) 水平摩擦阻力作用下,半刚性基层的弯沉在基层中部区域基本为0,在接近端部区域迅速增大,曲线出现凸起,而后弯沉降低为0出现反弯现象,并在基层端部达到最大值,其最大值随着ku的增加而增加、kv的增加而减小。
3) 对比分析干缩应力模型的解析解和简化解,结果表明基层长度L、基层厚度h及ku变化时,在基层中间区域干缩应力解析解和简化解的比值较为稳定,接近1,在基层端部的干缩应力比值有所变化,但由于基层端部的干缩应力不是基层开裂的决定性因素,因此,在对施工硬化阶段基层的最大干缩应力进行计算时,可采用简化解进行估算。
