基于多均匀圆阵的中心对称平滑算法
2018-10-11谈文韬黎仁刚
谈文韬, 黎仁刚, 林 明*
(1.江苏科技大学 电子信息学院, 镇江 212003)(2.中国船舶重工集团有限公司 第七二三研究所, 扬州 225101)
由于现代战场电磁环境的日益复杂,超分辨测向技术以其优越的算法性能得到了广泛关注,并且该类算法的研究热点逐渐从理论研究转向了工程实现[1-2].为了使测向系统适应复杂的电磁环境,文献[3]中采用空间平滑算法与MUSIC算法[4]相结合的方法,成功地解决了相参(干)信号的测向问题.该方法实现简单,是一种经典的解相参(干)方法,但仅适用等距阵列,且有较大的孔径损失.为了使解相参(干)算法适应不同的阵列形状,并减少天线阵列的孔径损失,学者们提出了大量的改进算法[5-8],该类算法通过模式空间变换、虚拟内插、空间平移等手段增强了算法的适应范围与测向性能.然而将该类改进算法应用于二维阵列时,至少需要两个方向上的平滑子阵[9-10],存在模糊伪峰增强、所需阵元数多、布阵空间要求高,以及计算量急剧增加等问题,大幅增加了方案的实现难度与实现成本.
在前后向空间平滑算法[11]中,从前后两个方向在一维线阵中选取子阵,使得可选取的子阵数为原来的两倍,即将阵元的利用率变为原来两倍,有效地降低了天线阵的孔径损失.但文献[11]中的空间平滑算法仅能应用于一维阵列.
为了降低二维相干信号测向的实现成本,降低孔径损失,增加阵元利用率,结合一维前后向平滑算法的特性,将其推广到具有镜像对称特性的二维平面阵列测向算法中,提出了一种中心对称平滑(central symmetry smoothing, CSS)算法.该方法能够有效降低二维空间平滑算法所需的阵元数量,降低工程实现成本.文中以均匀圆阵(uniform circular array, UCA)为例,对算法进行分析与仿真.
1 阵形分析
1.1 中心对称子阵
以5元均匀圆阵为例,入射信号与圆心的波程差,可视为各阵元在入射方向上的投影点到圆心的距离.通常,同一平面内阵元在来波方向上的投影顺序不受入射信号俯仰角影响[12].利用这一原理,将入射波降至一维平面内进行分析.对与基准子阵中心对称的矩阵进行同样的投影分析,如图1.

图1 5元中心对称均匀圆阵Fig.1 Central symmetry UCA with 5 sensors
图1中,天线阵在空间内垂直放置,y为水平方向,z为垂直高度.箭头方向为入射波方向,三角形为天线阵元,与阵元对应的圆点为阵元在入射方向上的投影.图中可以看出,两圆阵对应的阵元在随机来波方向上的投影间隔相等,排列顺序相反,即由波程差引起的相位差相反,在接收数据上反映为共轭(反相)关系.因此对中心对称子阵接收数据取共轭,与基准子阵接收数据的阵列流形一致.
根据这一特点,在布阵时,每个子阵中可以共用两个阵元,且镜像子阵可随基准子阵旋转排列,能够有效降低阵元数量,并缩小布阵所需空间.该镜像对称特性适用于任何子阵.
1.2 虚拟子阵
偶数均匀圆阵本身具有中心对称特性,因此每个偶数UCA都可以根据中心对称特性,以共轭转置的方式构造出一个虚拟子阵,能够大大减少空间平滑所造成的孔径损失.在阵元数一定的情况下,能够增加相干信号的解析数目,并提高测向精度.
图2中,真实阵元序号与中心对称虚拟阵元序号一一对应.根据文献[12],在实际应用中,偶数UCA的抗模糊性能远远差于奇数UCA,而必须使用偶数阵时,为了降低模糊,通常选取阵元数≥10的偶数UCA作为子阵.

图2 偶数均匀圆阵与虚拟子阵Fig.2 Even UCA and virtual sub-array
2 MUSIC算法
假设M元任意天线阵列的所有阵元均位于坐标系XOY平面内,第k个阵元坐标为(xk,yk,0),第i个窄带信号波长为λi,来波方向为(θi,φi),如图3,则第k个阵元到圆心(即原点)的波程差Δrik为:
Δrik=(xkcosθi+yksinθi)sinφi
(1)
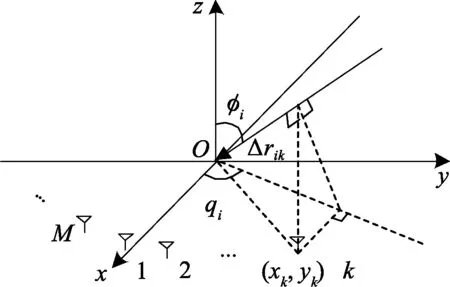
图3 阵列波程差Fig.3 Wave-way difference of array
天线阵列的接收公式为:
(2)
A=[α1,α2,…,αp]
(3)
s(t)=[s1(t),s2(t),…,sP(t)]
(4)
x(t)=As(t)+n(t)
(5)
式中:P为信号源数目;s(t)为P个入射信号的集合;x(t)为M个阵元处接收信号的组合;αi(θi,φi)为阵列的方向矢量;A为天线阵的阵列流形;n(t)为接收数据的噪声矩阵.
MUSIC算法基本原理为:
Rxx=E[x(t)x(t)H]=ARssAH+σ2IN=
UsΣsVs+UnΣnVn
(6)
(7)
(8)
式中:Rxx为接收数据的协方差矩阵;Rss为入射信号协方差矩阵;σ2为噪声功率;IN为单位矩阵;Us、Un分别为奇异值分解后得到的信号子空间与噪声子空间,上标^表示极大似然估计;PMUSIC为空间谱.
3 中心对称平滑算法
根据中心对称特性排布阵列,以3个7元UCA为例(图4).

图4 多7元均匀圆阵Fig.4 Multi-UCA with 7 sensors
图4中,分别以1、1’、1”,表示子阵①、子阵② 、子阵③ 的起始阵元,子阵内箭头所示方向为子阵阵元顺序.
对于任意阵列,设第i个与基准阵同向的子阵接收为xri,共有I个同向子阵,第k个中心对称子阵或虚拟子阵接收为xvk,共有K个.在该布阵方法中,相邻子阵至少能复用两个阵元,所以共能复用2(I+K-1)个阵元,而传统布阵方法的相邻阵列通常只能复用1个阵元.该布阵方法尤其适合子阵较多,且子阵非规则的情况.
首先对中心对阵子阵与虚拟子阵的接收数据做共轭反相处理,求所有子阵的自相关矩阵.
(9)
在无噪声理想条件下,对于任意i、k有Rri=Rvk.
对各子阵的自相关矩阵进行求和平均.

(10)
将式(10)所得的平滑后协方差矩阵带入常规MUSIC算法,即可完成对相干信号的求解.
CSS算法的基本流程可总结为:① 选定基准子阵,根据中心对称特性设定其他子阵,并确定对应阵元位置;② 对中心对称子阵或虚拟子阵接收数据进行反相处理;③ 计算各子阵的自相关矩阵;④ 对所有自相关矩阵求和取平均后,使用MUSIC算法进行方向估计.
4 性能分析
试验带宽为2 MHz,中心频率为18 GHz,调频斜率为200 kHz/us,最大信噪比为20 dB,其他呈3 dB递减的线性调频信号作为入射仿真信号,采样频率为80 MHz.
4.1 CSS算法的正确性
采用图4所示阵列,圆阵半径为10.4倍半波长,两子阵距离为9.4倍半波长,子阵间隔远远超过了常规空间平滑算法中子阵间隔半波长的限定.对3个方向分别为(-20°,10°)、(-17.5°,12.5°)、(-10°,12°)的相干入射信号进行算法仿真试验,空间谱扫描步长为0.25°,所得空间谱如图5.

图5 CSS算法空间谱Fig.5 Spatial spectrum of CSS algorithm
图5中,标注谱峰的X、Y、Z分别对应俯仰角、方向角和空间谱幅度.图中3个标注谱峰与入射信号方向一致,验证了算法的正确性;图中3个入射波非常接近,算法能够准确估计出小角度差值的相参(干)入射信号的来波方向,说明该算法具有较高的分辨率与估计精度;同时算法计算所得的空间谱相对平滑,子阵的选择较好地抑制了模糊伪峰的幅值.
4.2 虚拟子阵解相干能力
采用两个6元均匀圆阵,选取构造4个子阵,对3个方向分别为(-10°,10°)、(-7.5°,26.5°)、(0°,24°)的相干入射信号进行算法仿真试验.为了方便分析,减少模糊谱峰带来的影响,将谱峰搜索范围缩小到原来的四分之一,同样以0.25°为扫描步长,所得空间谱如图6.

图6 含虚拟子阵空间谱Fig.6 Spatial spectrum with virtual sub-array
图6中,算法仅用2个本身具有中心对称结构的物理子阵,以及构造出的2个虚拟子阵就能准确估计出3个相干入射信号的二维来波方向,极大减少了二维空间平滑算法所需的阵元数量.图6边缘处出现了模糊谱峰,说明该算法选取的子阵抗模糊性能较差,需要对子阵的选取作进一步研究.
5 结论
以相干信号二维测向的工程应用为目的,将一维的虚拟平滑算法推广到二维平面阵列.对于任意阵列,算法能够减少空间平滑所需的阵元数量;尤其对于本身具有中心对称结构的子阵结构,算法降低了平滑所需的子阵数量,有效地降低了二维空间平滑算法布阵的空间需求与实现成本,对算法的工程实现具有指导意义.目前,本身具有中心对称结构的子阵结构的抗模糊性能较差,子阵的具体选择有待进一步研究.
