5000m3/h非自航绞吸挖泥船全船结构振动特性分析
2018-10-11毛砚辉夏利娟
毛砚辉,夏利娟
(上海交通大学 海洋工程国家重点实验室,上海 200240)
绞吸挖泥船作为一种工程船,有着不同于常规船型的结构特点.因其特殊性,首尾均有很大的开槽来安置桥架和台车,中间主甲板上设计有长的较为发达的上层建筑,机舱和泵舱主甲板上设置有大开口,船体上放置复杂工程设备[1].工作状态时,与常规船舶自由状态不同,其钢桩插入地底将船舶固定,绞刀与土质接触处形成一定的约束,这一系列结构布置都会使其在振动特性问题上不同于常规的船舶.同时绞吸挖泥船处于工作状态时,需要有一定的稳定状态,绞刀切削岩石会对船体产生激励作用,故需对绞吸挖泥船进行振动特性分析.
采用大型通用有限元软件MSC.Patran/Nastran,对某5 000 m3/h非自航绞吸挖泥船进行了全船总振动特性评估和研究.绞吸挖泥船有拖航出港、到港、作业出港和到港4种典型工况,拖航与作业工况因钢桩和桥架等重要设备状态不同,质量分布与边界条件不同,出港和到港装载不等量燃料及淡水,因质量不同,故需计算比较该船4种工况的固有模态差异,并针对作业工况下的船舶振动特性进行评估分析;在此基础上,分析不同附连水质量计算方法(刘易斯图谱法和虚拟质量法)对船舶振动模态的影响;建立3种不同的有限元模型,分析上层建筑对船体总振动的耦合作用,以期对该类型船舶的振动特性评估提供参考.
1 模型简介
模型取自一艘单舷侧、艏艉单底、中部双底的非自航绞吸挖泥船.主船体首部有桥架开槽,尾部有钢桩台车开槽.拖航状态时,钢桩、桥架水平搁置;作业状态时,钢桩竖直插入地底将船舶固定,桥架与船体呈45°,同时绞刀切割绞松土质时与土质接触处形成一定的约束,具体见图1、2.该船主尺度垂线间长Lpp=98.0 m,型宽B=21.1 m,型深D=6.3 m,吃水d=4.5 m,出港时排水量Δ1=8 072 t,到港时排水量Δ2=7 427 t.

图1 拖航状态船舶总布置Fig.1 General layout of the ship in towing condition

图2 作业状态船舶总布置Fig.2 General layout of the ship in working condition
对全船结构进行了详细的有限元建模,桥架、钢桩、台车、门架等主要设备按照各自质量、质心和安装部位,在质心处建立集中质量单元,并将此质量单元通过多点约束MPC传递到各安装部位.滑油泵等小型设备,通过调整船体材料密度来增加,柴油舱等舱室内液体质量以及压载水质量则通过质量点模拟的方法,将相应质量加到对应舱壁和底板上.所有设备及货物加载后全船有限元模型见图3.
2 总振动特性计算分析
为了分析非自航绞吸挖泥船总体振动特性,以

图3 全船有限元模型Fig.3 Finite element model of the whole ship
整船结构为计算模型,选取拖航出港、到港和作业出港、到港4个典型工况.由于不同于常规船型的自由状态,绞吸挖泥船在工作时,钢桩和绞刀会对船体产生一定的约束作用,为了保持和实际工作条件相一致,分别约束钢桩与主船体连接部位单元节点的3个线位移以及桥架重心处单元的3个线位移.
考虑到流体介质对船体浸水表面的影响,采用附连水质量来模拟流——固耦合状态,以便分析该船体在水中的振动特性[2].现采用刘易斯图谱法计算附连水质量.船舶垂向振动,计算剖面处单位长度上附连水质量为[3]:
(1)
式中:Cv为考虑船体剖面形状的无因次修正系数;K为考虑船长和船宽b之比以及振动阶次的三维流动系数;αv为浅水修正系数.
船舶水平振动时附连水质量为:
(2)
各系数与垂向振动时类似.
由于船艏艉开槽,形成两个片体,类似双体船,故引用双体船垂向振动附连水质量计算公式,该公式引入修正系数φ加以修正[4]:
(3)
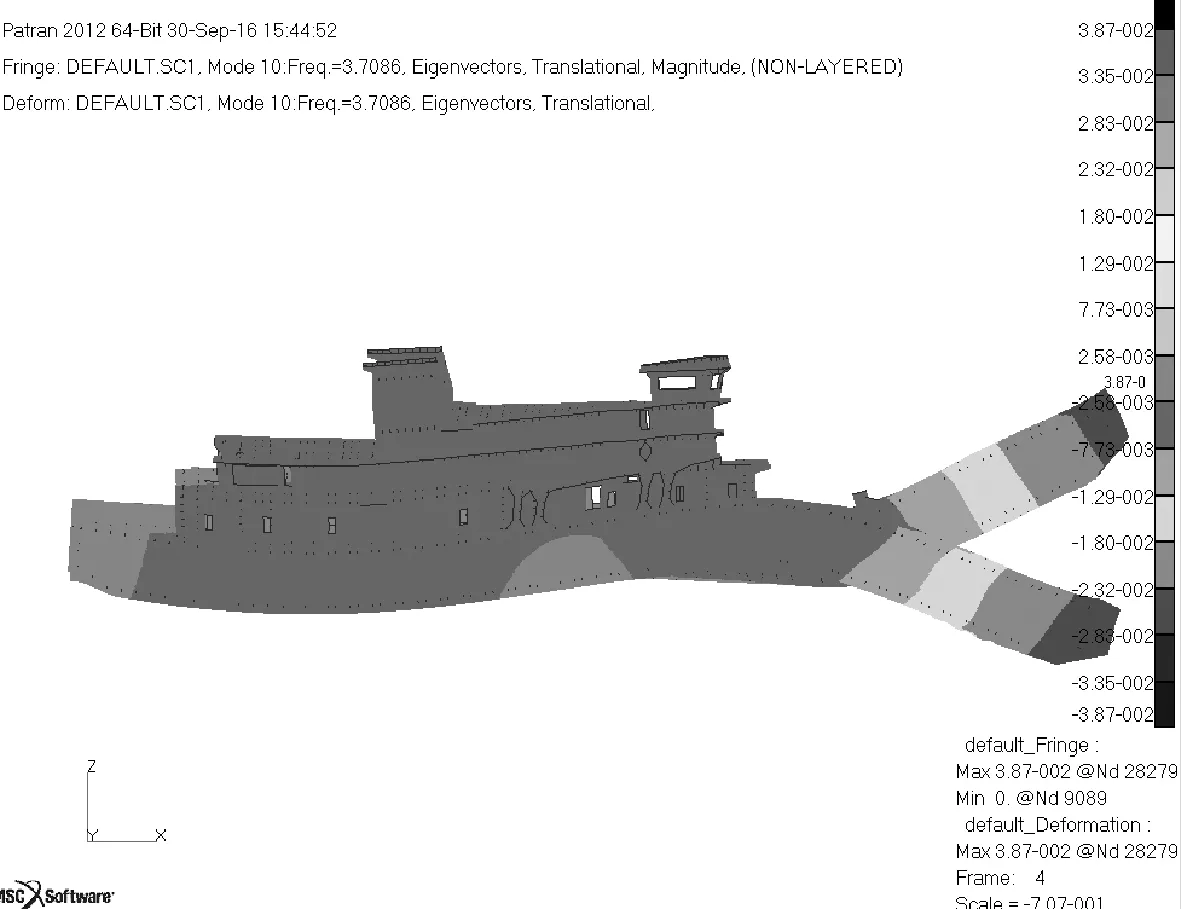
式中:当0 图4 修正系数φFig.4 Correction coefficient φ 根据本船结构特点,将船体沿船长方向分成不等间距六段,中间单体部分分为段间距较大的两段,艏、艉开槽双体部分型线变化较大,分别分成段间距较小的两段,并考虑双体的影响引入修正系数φ.以作业出港垂向振动为例,各系数取值见表1.根据以上公式和步骤分别计算出本船单位长度出港和到港的垂向和水平振动附连水质量,以质量点形式添加到水面以下每个肋位节点上. 4种工况振动特性计算结果见表2,部分振型见图5~8. 表2 振动特性计算结果Table 2 Calculation results of vibration characteristics 图5 一阶扭转振动(拖航出港工况)Fig.5 First order torsional mode (towingcondition of leaving port) 图6 一阶扭转振动与一阶水平振动耦合(作业出港工况)Fig.6 First order torsional mode coupling with first order horizontal mode(working condition of leaving port) 图7 二阶垂向振动(拖航到港工况)Fig.7 Second order vertical mode (towingcondition of arriving port) 图8 二阶垂向振动为主,艏部开槽区片体反向垂向振动、水平振动耦合(作业到港工况)Fig.8 Second order vertical vibration coupling with backward vertical and horizontal vibration of the demihull in the bow(working condition of arriving port) 从表2和图5~8的结果对比可以看出:拖航状态和作业状态下,因质量分布和边界条件不同,振动特性有较大差别;对应振型下,拖航状态振动频率比作业状态振动频率高.同时,拖航状态下,除去艏部开槽区片体的局部振动,其他振型都相对独立,作业状态下,因钢桩和绞刀对船体的约束,总体振动与艏艉开槽区片体振动发生耦合,振型不纯,出现很多耦合振型. 船舶处于作业状态时,存在绞刀激励,需评估其振动特性避免共振.绞刀挖掘岩石主激振频率可近似为[5]: (4) 式中:f为绞刀激励频率,Hz;z为绞刀刀臂数,z=6;n为绞刀转速,常用转速为30 r/min.由式可知,在常用转速下,绞刀激励频率近似取为f=3 Hz.由计算结果可知,该船的前四阶振动频率与激励频率错开率均大于13%,满足工程精度的要求. 附连水质量对结构振动特性的影响很大,以往国内外学者在这一方面做过很多研究[6-7].船体振动总质量由船舶有效质量与附连水质量两部分组成.附连水质量与船体本身质量为同一量级,故必须考虑附连水质量.如何准确地模拟附连水质量,关系到能否准确进行船舶固有模态的计算[8].对于一般常规船型,通用的计算附连水质量方法有刘易斯图谱法和虚拟质量法等.绞吸挖泥船结构复杂,首尾开槽,工作状态时有钢桩约束,需对其进行一定的研究分析.文中通过比较刘易斯图谱法和虚拟质量法两种不同的附连水质量计算方法来讨论其对非自航绞吸挖泥船振动特性的影响. 虚拟质量法[9-11]的基本原理是通过增加一个附加质量矩阵,实现不可压缩流体对结构的作用.流体中的结构振动模态有限元计算方程为: (5) 假设流体是各向同性且不可压缩的液体,忽略结构体表面重力的影响,且结构体的运动速度很低.根据流体力学的连续性方程、运动方程和能量方程,采用Helmholtz方法求解Laplace方程可以得到速度势和压力场的有限元形式解分别为: (6) (7) (8) (9) 式中:F为节点压力;α,β分别为式(6、7)积分后的值. 根据牛顿第二定律,力矩阵、质量矩阵和加速度矩阵之间的关系式为: (10) 将式(8、9)代入式(10)中得到虚拟质量矩阵为: MA=βα-1 (11) 在获得附加质量之后,就可以通过模态分析计算出结构在水中的固有频率和振型. 虚拟质量法考虑了船体与水流之间的相互影响,故以虚拟质量法计算结果为基准,统计拖航出港和作业出港工况下的船舶振动特性以及刘易斯图谱法相对虚拟质量法的差值百分比,结果见表3. 表3 不同附连水质量计算方法下振动特性比较Table 3 Comparison of vibration characteristics under different calculation method of added water mass 由计算分析结果可知: (1) 不同附连水质量计算方法——刘易斯图谱法和虚拟质量法计算所得振动特性有一定的差别,且随着阶次递增,垂向振动数值差异增大. (2) 相对来说扭转振动的数值差异较大,说明用垂向振动附连水质量代替扭转振动附连水质量误差较大[12]. (3) 作业出港工况下模型振动数值差异相较拖航出港工况下为大,考虑到作业状态下振型多为耦合情况,而刘易斯图谱法计算所得的附连水质量仅对应于单一振型. (4) 从总体来看,两种方法计算所得固有频率数值差异较小,均在10%以内,满足工程精度的要求. 目前对上层建筑振动的研究有很多,文献[13]中对船舶上层建筑有限元动力计算模型进行了研究;文献[14]中对船舶上层建筑整体振动有限元建模方法进行了研究讨论;文献[15]中应用ANSYS计算了VLCC上层建筑固有频率因模型化方法等原因导致的计算误差,研究了上层建筑重量、重心和板材厚度等对固有频率的影响并讨论了几种可行的提高固有频率的方案.以上研究内容侧重点集中于计算模型范围对上层建筑振动的影响,对于上层建筑对船舶总体振动的影响的研究仍较少.现阶段在分析船舶总体振动时,较多的采用主船体模型,忽略上层建筑,非自航绞吸式挖泥船结构形式特殊复杂,上层建筑较发达,需对上层建筑对船体总振动的影响进行研究讨论,确定简单合理的上层建筑简化模型. 文中研究对象为5 000 m3/h非自航绞吸挖泥船,该船中部主甲板上设4层上层建筑:第1层纵骨架式起居甲板室,长49 m,占全船总长50%;第2层横骨架式船长甲板室,长45.5 m,占全船总长46.43%;第3层横骨架式操纵甲板室,长27.3 m,占全船总长27.86%;顶层甲板长度很短.为了分析上层建筑对船舶总振动的影响,建立了5种有限元模型:模型1为包括所有上层建筑在内的全船结构模型;模型2为主船体和第一、二层上层建筑;模型3仅主船体和第一层上层建筑;模型4不含上层建筑结构,仅将上层建筑质量按其真实分布,以质量点的形式施加在上层建筑与主甲板连接的单元节点上;模型5仅主船体部分,忽略所有上层建筑.具体见图9~13. 图9 模型1(全船结构)Fig.9 Model 1(whole ship structure) 图10 模型2(主船体+第一、二层上层建筑)Fig.10 Model 2(main hull+the first and second floor of the superstructure) 图11 模型3(主船体+第一层上层建筑)Fig.11 Model 3(main hull+The first floor of the superstructure) 图12 模型4(主船体+上层建筑质量)Fig.12 Model 4(main hull+superstructure quality) 图13 模型5(主船体)Fig.13 Model 5(main hull) 为了分析上层建筑简化模型对船舶总体振动模态的影响,以刘易斯图谱法计算附连水质量,分别计算5种模型在拖航出港和作业出港工况下的结构固有模态,并统计了各个模型相对整船模型1的频率差值百分比,计算结果见表4. 表4 不同模型振动特性比较Table 4 Comparison of vibration characteristics between different models 由表4可以分析得知: (1) 对垂向振动和扭转振动而言,模型1、4振动频率数值差异较大,模型4、5频率值较为接近,而模型1、4质量大小相同,刚度不同,模型4、5刚度相同,质量不同,说明对于该类非自航绞吸挖泥船,上层建筑的刚度对垂向和扭转振动影响较大,质量对垂向和扭转振动影响较小;同时也说明该类非自航绞吸挖泥船其上层建筑垂向和扭转刚度较大. (2) 拖航出港工况相较于作业出港工况频率数值差异要大,考虑到作业出港工况下,钢桩和绞刀对主船体有一定的约束作用,导致上层建筑对主船体振动模态的影响减小. (3) 总体而言,上层建筑对船舶总体振动模态的影响垂向振动大于扭转振动. (4) 模型4、5相对模型1的频率数值差异较大,在20%左右;模型2、1振动频率基本相同;模型3相对模型1的频率数值差异小,在10%以内.为了简单并准确地计算船舶振动特性,避免低阶共振,建议采用主船体加首层上层建筑模型. 文中以5 000 m3/h非自航绞吸挖泥船为研究对象,对其进行了全船总振动特性分析,讨论了不同工况条件下船舶总振动固有频率和振型的区别,分析了不同附连水质量计算方法对船舶总振动固有特性的影响以及上层建筑对船体总振动的耦合作用,得到如下结论: (1) 拖航和作业状态下,因质量分布和边界条件不同,船舶振动特性会有较大差别,具体表现:对应振型下,拖航状态振动频率比作业状态振动频率高;作业状态下钢桩和绞刀对船体有约束作用,出现很多耦合振型.作业状态下船舶振动频率与激励力频率错开率高于13%,满足工程精度要求. (2) 刘易斯图谱法和虚拟质量法计算附连水质量对振动模态有一定的影响,相对于拖航状态,工作状态时振型更为复杂,出现很多耦合振型,故对其影响更大.但总的来说两者计算结果相差不大,满足工程精度的要求. (3) 上层建筑对该类船舶总体振动模态的影响表现在垂向振动大于扭转振动,评估船舶振动特性时,建议采用主船体加首层上层建筑模型.




3 附连水质量对振动特性的影响

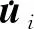
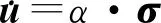


4 上层建筑简化模型对船舶总振动模态的影响
4.1 计算模型





4.2 上层建筑简化模型对船体总振动的影响分析

5 结论
