利用空间平滑的协方差秩最小化DOA估计方法
2018-10-11王洪雁房云飞裴炳南
王洪雁,房云飞,裴炳南
(1. 大连大学 辽宁省北斗高精度位置服务技术工程实验室,辽宁 大连 116622;2. 大连大学 大连市环境感知与智能控制重点实验室,辽宁 大连 116622)
在雷达、移动通信、声呐等领域,波达方向角(Direction Of Arrival,DOA)估计一直是热门研究方向之一[1-2].在众多波达方向角估计方法中,以多重信号分类(MUltiple SIgnal Classification,MUSIC)为代表的子空间类算法[3]具有较高的角度估计精度和分辨力.然而,在相干信号和非均匀噪声条件下,由于信号协方差矩阵秩亏及其主对角元素非均匀性导致协方差矩阵特征空间的主特征矢量无法张成整个信号空间,从而导致基于子空间的波达方向角估计算法性能显著下降[4-5].为改善非均匀噪声下波达方向角估计性能,文献[6]提出一种最大似然(Maximum Likelihood, ML)估计算法,通过求解信号和噪声的对数似然函数以实现波达方向角估计,但最大似然算法的较大运算复杂度限制了该算法的应用.文献[7]提出一种改善的协方差矩阵稀疏表示波达方向角估计方法,主要通过数学线性变换剔除非均匀噪声成分以消除非均匀噪声影响,但算法剔除操作将会导致协方差部分信息损失.基于此,文献[8]提出一种基于矩阵补全的波达方向角估计(Matrix Completion based MUSIC,MC-MUSIC)方法,基于矩阵补全理论[9]将协方差矩阵重构为无噪声信号协方差矩阵以抑制非均匀噪声的影响,而后通过传统MUSIC算法实现波达方向角估计.然而,该算法没有考虑相干信号对波达方向角估计性能的影响.
近年来,众多相干信号和非均匀噪声条件下的波达方向角估计算法相继被提出.文献[10]基于传统空间平滑理论[11]提出一种改进的空间平滑算法,首先将子阵输出的自相关矩阵进行互相关,而后基于前后向互相关矩阵的均值获得较好的信号空间谱估计.然而,该算法没有考虑非均匀噪声的情况,且由于将阵列分成若干子阵,使得阵列孔径减小,进而降低了算法的分辨率,从而限制了该算法的应用[12].文献[4]提出一种基于最小二乘和空间平滑的波达方向角估计算法,该算法通过迭代消除非均匀噪声影响,并利用空间平滑方法实现相干源波达方向角估计,具有较好的波达方向角估计性能,但算法需要迭代初始值选取,且计算量较大.文献[13]则提出一种协方差矩阵秩迹最小化(Rank and Trace Minimization,RTM)算法,利用协方差矩阵低秩特性将无噪声协方差矩阵低秩问题转化为噪声功率最大化问题,以此求得未知的非均匀噪声功率,而后利用接收信号和非均匀噪声协方差矩阵之差实现波达方向角估计.然而,在信号相干条件下,由于接收信号协方差矩阵秩进一步降低,可能导致算法所得协方差矩阵秩低于真实值,从而无法保证该算法的波达方向角估计性能[4].
针对上述问题,笔者基于空间平滑方法提出一种协方差秩最小化(Spatial Smoothing based Covariance Rank Minimization,SS-CRM)波达方向角估计算法.在非均匀噪声和相干信号下及在传统空间平滑方法基础上,所提算法将接收信号协方差矩阵分别左右乘交换矩阵以得到空间后向平滑协方差矩阵,从而降低信号的相干性,且平滑后的阵列孔径保持不变,保证了算法的分辨率; 而后基于平滑矩阵的低秩性,通过协方差秩最小化算法得到非均匀噪声功率,并利用空间平滑协方差和噪声协方差矩阵之差得到无噪声协方差矩阵,从而抑制非均匀噪声的影响;最后利用传统MUSIC算法实现波达方向角估计.
1 问题描述

(1)
其中,x(t)为接收信号矢量;a(θl)=[1,exp(-jα),…,exp(-j (M-1)α)]T,为第l个信源的阵列导向矢量;α= 2πdsinθl/λ,为相邻阵元之间的相位差;d和λ分别为阵元间距和信号波长,通常d≤λ/2;n(t)= [n1(t),…,nM(t)],为不相关的非均匀高斯噪声,且n(t)~CN(0,Q),Q为非均匀噪声协方差功率矩阵; 窄带信号sl(t)互不相关.
为便于推导,式(1)接收信号模型可改写为
x(t)=As(t)+n(t) ,
(2)
其中,A=[a(θ1),a(θ2),…,a(θL)]∈CM×L,为阵列流型矩阵;s(t)= [s1(t),s2(t),…,sL(t)],为信号波形矢量.假设M≫L.
对于J次快拍,式(2)可进一步表示为
X=AS+N,
(3)
其中,X=[x(1),x(2),…,x(J)]∈CM×J,为接收信号矩阵;S= [s(1),s(2),…,s(J)]∈CL×J,N= [n(1),n(2),…,n(J)]∈CM×J,分别为信号波形矩阵和非均匀高斯噪声矩阵.
基于式(3),接收信号协方差矩阵可表示为
RX=E[X(t)XH(t)]=APAH+Q,
(4)
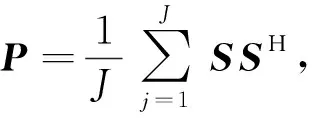
由式(4)可知,可通过子空间类算法对接收信号协方差RX进行特征空间分解以实现波达方向角估计.然而,当信源为相干信号时,将导致接收信号协方差矩阵秩亏,从而使得RX特征分解得到的特征值数目小于信源个数,进而无法有效地实现信号波达方向角估计[8].
2 传统的空间平滑方法
针对上述问题,文献[11]提出空间平滑方法以舒缓相干信号对波达方向角估计的影响.传统的空间平滑算法利用线阵平移不变性,将均匀线性阵列等同划分为D个子阵.若每个子阵包含O个阵元,可得M=O+D-1,且D≥L+1,O≥L+1,则第i个子阵输出可表示为
Xi,O=Ai,Oγi,lS+Ni,O,
(5)
其中,Ai,O,Ni,O分别是与第i个子阵对应的阵列导向矢量和噪声矢量;γi,l= diag{exp(jφi,1),exp(jφi,2),…,exp(jφi,L)},为对角旋转矩阵,diag{·}为对角化算子,φi,l= 2π(i- 1)dλ-1sinθl.
基于式(5),第i个子阵所得信号协方差矩阵可表示为
(6)
其中,Qi,O为子噪声功率矩阵.
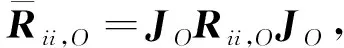
基于式(6),传统的空间平滑协方差矩阵可表示为
(7)
由式(7)可知,传统的空间平滑算法将线阵划分为D个子阵,可降低信号相干性影响,从而实现较好的相干信号波达方向角估计,但同时也降低了天线孔径,导致波达方向角估计分辨率下降.此外,在非均匀高斯噪声下,由于信号协方差特征分解会引起信号子空间泄漏,进而导致基于空间平滑的波达方向角估计性能严重下降[8].
3 基于空间平滑的信号协方差矩阵秩最小化波达方向角估计算法

Y(t)=JX*(t) ,
(8)
其中,X*(t)为X(t)的复共轭;J为交换矩阵,满足JHJ=1[4].
由式(8)可知,空间后向平滑信号Y(t)的协方差可进一步表示为
(9)
基于式(4)及式(9),空间平滑信号协方差矩阵可表示为
R=(RX+RY)/2=Rss+Qss,
(10)
其中,Rss和Qss分别为空间平滑无噪声协方差和非均匀噪声协方差矩阵.
基于式(10),空间平滑无噪声信号协方差可进一步表示为Rss=R-Qss.
为了利用凸优化方法求解式(10)中无噪声信号协方差Qss,基于矩阵优化理论,利用信号协方差低秩特性将上述问题转化为协方差矩阵秩最小化问题[8].基于此,为了利用秩最小化方法求解Qss以重构无噪声信号协方差矩阵,需要首先证明Rss为低秩矩阵.为此,提出如下命题.
命题1 如果信号s(t)互不相关,且信源数L远小于阵元数M,则R-Qss和Rss是一个低秩矩阵.
证明 阵列流型矩阵A的共轭转置左乘交换矩阵J,可得
JA*=AγM,l.
(11)
同理,由式(11)可得
(12)
由式(10)~式(12),可得rank(R-Qss)=rank(APAH),且Qss0,即Qss为半正定矩阵.
对于秩为L的矩阵R及实对角矩阵Λ,rank(R-Λ)≥L.由rank(APAH)=L可知,当Λ=Qss时,可得 rank(R-Qss)= rank(APAH)=L,则R-Qss和Rss为低秩矩阵,命题1成立.
由命题1可知,R-Qss为低秩矩阵,故可将R-Qss秩最小化问题[13]表示为
(13)
其中,Z+代表一个正定矩阵合集.
由于秩函数的非凸性使得式(13)难以求解,故可将式(13)最小化问题等价松弛为

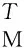
(15)
其中,1M=[1,1,…,1]T,为M×1的列矢量;qss=[q1,q2,…,qM].
基于式(14)及式(15),优化问题(13)可等价为如下的半定规划问题(SemiDefinite Programming, SDP),即
(16)
上述半定规划优化问题可用Matlab凸优化工具包(比如CVX[15])实现高效求解.
基于式(16),可得非均匀噪声功率qss估计值,即非均匀噪声协方差可重构为Qss= diag{qss}.由式(10)可知,空间平滑无噪声协方差矩阵可表示为
(17)

(18)
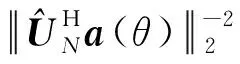
4 实验仿真及分析

实验1 考虑入射角度分别为-3°、10°和16°的非相干信号.图1(a)是4种算法的空域谱对比图,信噪比为 -5d B.由图1(a)知,在低信噪比条件下,传统的MUSIC、MC-MUSIC和RTM算法无法分辨10°和16°的两个目标,而SS-CRM算法可有效地分辨3个目标.图1(b)是4种算法的空域谱对比图,信噪比为 0 dB.由图1(b)知,由于非均匀噪声影响,传统的MUSIC算法不能分辨10°和16°的两个目标,而MC-MUSIC、RTM和SS-CRM算法均可分辨3个目标.此外,由图1还可知,与其他算法相比,所提算法具有较窄的主瓣,表明所提算法在非均匀高斯噪声和低信噪比条件下具有较好的波达方向角估计性能.

图1 信噪比为-5 dB和0 dB条件下的非相干信号空域谱对比图
实验2 考虑入射角度分别为-3°、10°和16°的信号,其中 -3° 和10°的入射信号相干.图2(a)是4种算法的空域谱对比图,信噪比为 -5 dB.由图2(a)知,在相干信号条件下,MUSIC、MC-MUSIC和RTM算法均不能有效地分辨3个目标,而SS-CRM算法由于对相干信号进行解相干,从而可正确地分辨3个目标.图2(b)是4种算法的空域谱对比图,信噪比为 0 dB.由图2(b)知,在非均匀噪声和相干信号条件下,SS-CRM算法可有效地分辨3个目标,且具有较窄的主瓣,而其他算法仅可分辨16°的目标.由此表明,与MUSIC、MC-MUSIC和RTM算法相比,所提SS-CRM算法在相干信号和非均匀噪声条件下亦具有较高的角度估计精度和分辨力.

图2 信噪比为-5 dB和0 dB条件下的相干信号空域谱对比图
实验3 考虑入射角度为-3°和16°的非相干信号和相干信号,信噪比为 -8~ 12 dB,步长为 2 dB,进行200次蒙特卡罗实验.图3为非相干信号、相干信号波达方向角估计均方根误差随信噪比变化的对比图.由图3(a)知,在非相干信号和非均匀噪声下,传统MUSIC算法的均方根误差相对较高,而MC-MUSIC和RTM、SS-CRM算法分别基于矩阵补全理论和协方差秩最小化方法抑制非均匀噪声,从而可显著降低波达方向角估计均方根误差.由图3(b)知,在相干信号和非均匀噪声下,4种算法的均方根误差均有所增加,但所提SS-CRM算法的均方根误差始终低于其余算法.由此表明,与其余算法相比,无论在非相干或相干信号条件下,所提算法的均方根误差均低于其他3种算法,表明所提方法具有较好的角度估计精度.另外,由图3还可知,在低信噪比条件下,所提算法的均方根误差明显优于其他算法,表明所提算法在相干信号和低信噪比条件下具有较好的波达方向角估计性能.

图3 波达方向角估计均方根误差随信噪比的变化对比图
实验4 考虑入射角度分别为-3°和16°的相干信号,信噪比为 0 dB,J= [100: 1 100],进行200次蒙特卡罗实验.由图4可知,随着快拍数增加,所提SS-CRM、MUSIC、MC-MUSIC及RTM算法的均方根误差均逐渐降低,且所提SS-CRM算法的均方根误差显著低于其他算法.由此表明,在相干信号及非均匀噪声条件下,所提算法的波达方向角估计性能明显优于传统的MUSIC、MC-MUSIC和RTM算法,具有较高的角度估计精度.

图4 波达方向角估计均方根误差随快拍数的变化对比图图5 波达方向角估计均方根误差随WNPR的变化对比图


图6 所提算法的信号空间谱对比
实验6 为验证所提算法在不同协方差矩阵条件下的波达方向角估计性能,实验中非均匀噪声协方差功率矩阵Q之迹保持不变,即 tr(Q)= 30,其他参数设置如实验1(b).图6为不同协方差矩阵条件下所提算法运行10次所得信号空间谱估计.由图6可知,在不同协方差矩阵条件下,所提算法均可有效地辨识3个目标角度,且具有较高的主瓣和较低的旁瓣.由此表明,所提SS-CRM算法在不同协方差矩阵条件下均具有较好的波达方向角估计性能和噪声鲁棒性能.
为较全面地评估上述算法的性能,在此将分析所提算法的运算时间(完成一次波达方向角估计所需的时间).在仿真中,除快拍数外,其他参数均为定值.由表1可知,随着快拍数增加,各算法处理数据量增大,则4种算法完成一次波达方向角估计所需的时间均逐渐增加.由于所提SS-CRM、MC-MUSIC和RTM算法利用信号协方差低秩特性以消除非均匀噪声影响,则此3种算法的运算时间略高于传统的MUSIC算法.此外,所提算法的运算时间近似等于MC-MUSIC和RTM算法.需要说明的是,所提算法不仅可抑制非均匀噪声影响,还可实现相干源解相干,保证了非均匀噪声和相干信源条件下的波达方向角估计性能.

表1 算法运算时间与快拍数个数的关系表s
5 结 束 语
针对传统的波达方向角估计算法在相干信号及非均匀噪声条件下角度估计精度差的问题,基于空间平滑理论,笔者提出一种信号协方差矩阵秩最小化波达方向角估计算法.该算法基于空间平滑方法构建平滑协方差矩阵以降低信号的相干性; 而后利用平滑协方差矩阵低秩性将接收信号协方差矩阵重构为无噪声协方差矩阵,以改善相干信号条件下波达方向角估计精度,并抑制非均匀噪声的影响.仿真结果表明,与传统的MUSIC、MC-MUSIC和RTM算法相比,所提算法在相干信号和非均匀高斯噪声条件下,具有较好的波达方向角参数估计性能.
