基于数学形态谱的逆变器功率管开路故障诊断
2018-10-10宋平岗林家通周振邦
宋平岗,章 伟,陈 欢,林家通,周振邦
(华东交通大学电气学院,南昌 330013)
电力电子技术的日益发展促使由电压源型脉宽调制逆变器供电的变频调速系统在工业生产中得到广泛的应用,但是工业生产过程中恶劣的工作环境容易造成功率开关器件的损坏。相对于传统的电机驱动系统而言,由电压源型脉宽调制的逆变器供电的变频调速系统的可靠性要高很多,尽管如此,此类调速系统逆变器的仍然无法实现完全可靠。并且逆变器故障修复时间较长,且功率管的开路故障伴随着电机的持续运行,发觉不易,容易诱发二次故障导致整个电气传动系统的瘫痪,存在很大的安全隐患[1-3]。为了减小逆变器故障带来的损失,避免二次故障的发生,近年来逆变器故障诊断技术受到研究人员的广泛关注,提出了很多诊断方法[4-9]。
现阶段国内外已有的逆变器故障诊断方法主要分为基于模型、基于信号和基于知识3种。其中,以研究逆变器故障输出电流或电压中隐含的故障信息居多。文献[10]提取故障电流的矢量轨迹,发现不同故障下逆变器输出电流的矢量轨迹呈不同的半圆,以此作为故障特征实现故障分离。但空载与轻载时易受误差与噪声影响;文献[11]中提出利用正常逆变器与实际逆变器输出电压信号的差异结合最小二乘估计得出谱残差,利用多层感知神经网络对逆变器故障进行分离,从而实现逆变器的故障诊断;文献[12]中提出一种基于逆变器直流电流的故障诊断方法,通过比较故障前后直流侧电流的频谱来实现单管开路故障的定位,该方法简单快速,但是难以实现双管开路故障的精确定位。除此之外,利用传统的信号处理方法如傅里叶变换、小波分解、模糊识别等技术[13-15]对输出电流或电压信号进行处理也能够进行故障分离,实现故障管的诊断与定位。
本文利用形态学多尺度形态谱对故障波形进行分析,实现故障管的准确定位。与传统的频域、时域的非线性分析方法不同,形态学多尺度形态谱可以定量的对信号在不同尺度下的形态特征进行刻画,目前已在输电线路故障检测[16]、振动信号处理方面得到广泛的应用[17-19]。本文从故障波形出发,针对不同故障下逆变器输出电流波形的缺失与畸变情况的差异,对故障信号进行多尺度形态开运算计算,得出1~40尺度下的形态谱值,以其作为故障特征输入ELM神经网络,结合简单的故障判别机制,以期实现故障的分离。
1 多尺度形态学与形态谱
1.1 多尺度形态学
形态滤波理论是基于信号的几何特性以不同的结构元素对象进行形态变换从而达到信号处理的目的。膨胀和腐蚀是数学形态学最基本的两种运算,其定义如下:f(n)、g(n)是定义在离散域 F={0,1,…,N-1}及 G={0,1,…,M-1}的实函数(N>M),其中f(n)是待处理信号,g(n)为结构元素。记腐蚀运算符号为Θ,膨胀运算符号为⊕,则可定义
腐蚀运算为

式中,m∈(0,1,…,M-1)。
膨胀运算为

多尺度形态学以形态开运算与形态闭运算为基本运算,其表达式为

如果将结构元素g进行自身的多次膨胀运算得数学形态学多尺度变换,则有

其中,ng=g⊕g⊕…⊕g(n-1 次),n 为尺度。
1.2 数学形态谱
数学形态谱能够对信号的形状进行定量描述,形态谱刻画的是信号在不同尺度结构元素形态学开闭运算下信号形状变化的信息,信号形状的差异导致其形态谱特征亦不同。数学形态谱定义如下:
设 f(x)为非负函数,g(x)为结构元素,则有信号 f(x)关于结构元素 g(x)的数学形态谱的定义,即

式中:S(f)为 f(x)在定义域内的有限面积,S(f)=f(x)dx。当 λ≥0 时,PSf(λ,g)为开运算形态谱;λ<0时,PSf(λ,g)为闭运算形态谱。
若f(x)为一维离散信号,结构元素选用扁平型元素,且所选取的形态尺度为连续整数值时,形态谱定义可以简化为

2 Elman神经网络原理
Elman神经网络算法是针对单隐含层前馈神经网络的新算法,该算法随机产生输入层与隐含层神经元的阈值,并且在训练过程中不再需要调整,只要对隐含层神经元个数加以设定就能得到唯一最优解。与传统的基于梯度下降的学习算法相比,该算法具有学习速度非常快,不会陷入局部极小,具有更好的泛化能力的优点。
Elman神经网络算法典型结构如图1所示,该网络算法以前馈链接为主要结构,包括输入层、隐含层以及输出层,其连接权可以进行学习修正;设外部输入时间序列为u(t),输入层神经元个数为p,网络输出为y(t),隐含层神经元个数为l,隐含层激活函数为g(x),则Elman神经网络的输入与输出的数学模型为
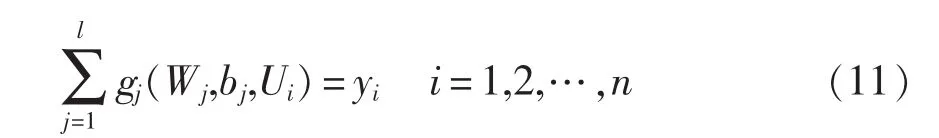
式中:W为输入层与隐含层之间的权值;η为隐含层与输出层之间的权值;b为隐含层神经元的阈值。本文中,隐含层激活函数选用sigmoid函数。

图1 典型Elman神经网络结构Fig.1 Structure of typical Elman neural network
3 逆变器故障分类及波形差异分析
3.1 逆变器故障分类
三相桥式电压源型逆变器如图2所示,在实际运行过程中,其功率管开路故障以单管开路及双管开路情况居多,3只功率管同时开路的情况极其少见,本文只针对逆变器单管开路以及双管开路故障进行诊断与区分。这样,逆变器功率管开路故障便可以分为:单管故障、同一桥臂两管故障、不同桥臂交叉两管故障以及不同桥臂同侧两管故障4大类。各种情况所对应的具体功率管故障见表1。

图2 三相桥式电压源型逆变器Fig.2 Three-phase bridge voltage source inverter

表1 逆变器IGBT开路故障分类Tab.1 Classification of open-circuit fault types in inverter IGBT
3.2 各类故障下波形差异分析
正常状态下,滤波后的逆变器三相输出电流波形均为正弦波,如图3所示。
当发生IGBT单管故障时,流经故障管T的电流将被截止,电流只能通过反向二极管D向直流侧反送电流,对应相的输出电流的波形将发生缺失,上桥臂功率管发生故障对应相的正半波电流缺失,下桥臂功率管发生故障对应相的负半波电流缺失。图4为A相上桥臂功率管故障输出波形。
对于开环控制的逆变器而言,单管故障对非故障相的输出电流波形影响较小,可视为与正常状态下的输出电流形状相同。

图3 无故障状态三相电流波形Fig.3 Three-phase current waveform in no-fault state

图4 T1开路时三相电流波形Fig.4 Three-phase current waveform when T1is under open-circuit fault
同一桥臂上下两只功率管开路故障时,由于故障相的上下桥臂功率管均开路,导致故障相的输出电流波形为直线,而非故障相受影响较小,波形视为与正常状态下输出电流波形相同,见图5。
不同桥臂交叉两只功率管发生故障时,除了故障相波形出现缺失外,非故障相波形发生严重畸变,如图6所示。不同桥臂同侧2只功率管发生故障时,对应故障相波形发生缺失,并且由于三相对称调制的原因,导致非故障相波形也出现波形缺失现象,如图7所示。
综上所述,逆变器功率管开路故障会使得各相电流波形出现4种情况:正半波电流缺失、负半波电流缺失、正负半波电流缺失与波形发生严重畸变,加之未出现波形缺失及畸变的正常正弦波形,逆变器三相电流输出波形可看做是上述5种波形的组合,若能够正确地区分上述5种波形,结合合理的故障判别机制便能够实现逆变器的功率管开路故障的诊断与定位。

图5 T1、T2管开路三相电流波形Fig.5 Three-phase current waveform when T1and T2 are under open-circuit fault

图6 T1、T4管开路三相电流波形Fig.6 Three-phase current waveform when T1and T4 are under open-circuit fault

图7 T1、T3管开路三相电流波形Fig.7 Three-phase current waveform when T1and T3 are under open-circuit fault
4 数学形态谱的逆变器开路故障诊断
为了验证多尺度形态谱能够有效地对逆变器各种开路故障下的输出电流波形进行区分,在MATLAB/Simulink里搭建开环PWM调制三相桥式电压源型逆变器模型,通过移除IGBT的驱动信号实现各种单管、双管故障的模拟,获取故障信号,见图 3~图 7。
4.1 逆变器故障波形形态谱分析与区分
根据数学形态谱定义,待分析信号f(x)为非负函数。由于波形的上下平移未改变波形形状,其形态谱值也不会发生变化。为了满足f(x)非负性的条件,将各输出电流信号向上平移,确保f(x)>=0结构元素选取扁平型结构元素。根据式(9)计算各输出电流信号的1~40尺度的归一化开运算形态谱值。图8为逆变器输出电流波形未缺失、正半波电流缺失、负半波电流缺失、正负半波电流均缺失以及波形严重畸变5种状态下的形态谱曲线。
形态谱曲线是对信号形态特征的反映。谱值大说明在该尺度下的结构元素与信号一致的特征信息就多,反之则少。逆变器功率管开路状态下输出电流的形态谱值是对其波形形状的反映,图8表明开路故障状态下出现5类故障波形的形态谱曲线形状各不相同。因此,可以利用5类故障波形归一化形态谱曲线的差异,取图8中各类故障波形的形态谱中的前11个形态谱值作为故障波形的特征向量输入ELM神经网络中进行识别,以期实现逆变器开路故障波形的区分。
通过改变逆变器直流侧电压值获取5类故障波形各20组,计算这100组原始信号在1~40尺度下的形态谱值,获取对应的形态谱曲线。5类故障波形共100组形态谱曲线中,将每类故障波形的前15组作为训练样本,剩余5组作为测试样本输入神经网络中。多次运行结果表明将归一化形态谱曲线中的前11个尺度下的形态谱值组成的输入向量便可以实现对故障波形的区分,既节省了训练时间又保证了准确率。神经网络隐含层数取20最宜。为了方便ELM神经网络区分各类故障需要对5类故障波形进行编号见表2。
将上诉100组数据输入神经网络中,神经网络输出的真实值与预测值的对比如图9所示,从图中可以看出,本文提出的方法对故障电流波形的区分率超过96%。

图8 逆变器输出电流波形形态谱Fig.8Pattern spectrum ofoutputcurrentwaveform from inverter

表2 故障波形编号Tab.2 Label numbers of fault waveforms
4.2 基于逆变器三相输出电流的故障判别机制
如果将无故障状态作为一种特殊故障,那么开环控制策略下的逆变器功率管单管、双管故障共有22种,单相输出波形形状有5种,而22种故障下的每一种三相故障电流均可视为5种波形中的3种组合,将5种故障波形按照表2进行编号,并以A相、B相、C相的顺序排列,22种故障的故障编号见表3(无故障状态下编号为:111)。

图9 真实值与预测值对比结果Fig.9 Comparison result between real and predicted values
表3中的故障编号是对三相输出电流波形的反映,由于22种故障状态下三相输出电流波形均不相同,则该故障编号便可成为故障判别的依据。收集逆变器的三相输出电流,按本文方法获取其故障编号,对照表1便能实现故障管的精确定位。

表3 功率管故障类别编号Tab.3 Label numbers of transistor’s fault types
5 实验数据验证
通过实验得到各故障波形(数据)如下。图10中的实验故障波形依次为正常电流信号、严重畸变电流信号、波形下缺失电流信号、波形上缺失电流信号以及上下半波电流均缺失电流信号。
利用本文方法对所得实验数据进行分析。设实验数据矩阵为Ai(i=1,2,3,4,5)为上文提及的5种不同的故障波形),在尺度为1下,也就是结构元素为g1=[0 0 0]时,利用式(3)对 Ai进行开运算得

在尺度为2时,结构元素g2=g1⊕g1,则有


图10 实验故障波形Fig.10 Waveforms of experimental fault

表4 实验数据的神经网络区分结果Tab.4 Diagnosis result of experimental data using neural network
由于A1i与A2i均为一维离散数列,则满足数学形态谱定义的简化条件可代入式(7),求解尺度为1下的数学形态谱值,即

式中,函数S为一维离散信号的面积计算函数。利用上述步骤可以得出实验得到的各故障波形1~40尺度下的形态谱值。
随机选取10组实验数据,计算其数学形态谱值,按照本文方法输入Elman神经网络进行区分,结果如表4所示。对照表2中的故障波形编号,可以得知本文方法对实验所得不同种类的故障数据能够进行有效的区分,验证了本文方法的有效性。
6 结论
(1)基于多尺度形态谱分析的逆变器故障诊断方法能够定量地对故障波形进行形态特征的描述,实现故障波形的区分,再结合简单的故障判断机制,实现了逆变器功率管开路故障的准确定位,为逆变器功率管开路故障诊断提供了一个新思路。
(2)基于多尺度形态谱的逆变器故障诊断方法以形态学基本运算为基础,该运算只涉及加减以及极值运算。相比于传统的逆变器功率管开路诊断方法,避免了坐标变换、傅里叶变换等复杂的数学计算,具有时延小、速度快的优点。
