非隔离型地铁机车工况模拟能量回馈系统

顾靖达，杨晓峰，郑琼林

（北京交通大学电气工程学院，北京 100044）

近年来，城市轨道交通因高效环保、轻便快捷等优点得以快速发展，在城市公共交通发展中占据重要地位，地铁和有轨电车等交通方式组成了庞大的城市轨道交通网络。由于城市轨道交通系统结构复杂、机车体积庞大、客流量大，不具备经常进行实验的条件[1-5]，在实验室模拟城市轨道交通机车的工作情况成为研究课题之一。

文献[6-7]提出用受控电流源或电阻代替机车的方法，用于牵引供电系统特点等方面的研究，但是这种方法只能模拟机车牵引工况的特点，无法反映机车再生工况的状态；文献[8]以模拟机车位置的改变为主要思路，用直流变换器的输出阻抗代表直流轨道的各个阻抗，调节直流变换器占空比改变输出阻抗的大小，从而实现改变机车位置的模拟，但存在牵引供电仿真系统结构复杂、运算量大的问题；文献[9]以力学知识为基础，分析机车每节车厢的受力情况，结合仿真软件得到机车的速度-距离曲线与速度-时间曲线，实现对机车的模拟；文献[10]依据牵引曲线对机车的运动情况进行模拟，以研究轨道杂散电流和对地电位的分布情况；文献[11-12]通过电机角速度的变化反映列车运行过程中负载的变化，得到相关表达式用于地铁牵引供电系统的仿真。

上述城市轨道交通机车模拟方法优势明显，但以软件仿真模拟为主，无法开展进一步硬件实验模拟。故本文基于电力电子化地铁机车的硬件模拟MLE（metro locomotive emulator）方法，提出非隔离型地铁机车工况模拟能量回馈系统（以下简称“模拟系统”），实现地铁牵引供电系统与地铁机车典型工况特性的模拟。本文首先介绍了MLE的拓扑结构及工作原理；在此基础上进一步分析了MLE的约束条件，提出改进的占空比控制策略。接着在DC 750 V牵引供电系统中对模拟系统的结构、工作特性与能量回馈过程进行分析与仿真验证，并对其经济性进行说明。为分析模拟系统的普适性，在DC 1 500 V牵引供电系统中对其工作原理与特性进行剖析验证。

1 MLE拓扑、原理及控制策略

1.1 拓扑结构

MLE由升压单元和降压单元组成，升压单元代表被试机车，降压单元代表陪试机车。为模拟被试机车的能量回馈过程，设置陪试机车将被试机车的输出能量回馈至牵引所，即被试机车的能量输入端。图1是MLE的拓扑结构示意，为方便后续分析，用箭头标示电流参考方向。

地铁机车有3种典型工况：牵引工况、再生工况与惰行工况。当地铁机车惰行时，牵引电流很小，辅助系统工作，相当于电流很小的牵引工况。若不考虑辅助系统的功率，牵引电流为0，相当于不工作。因此MLE主要考虑牵引和再生两种工况即可。

如图1所示，当开关K1和K2掷于位置1时，牵引能量输入被试机车，流过电感Lf1的电流为正，MLE模拟地铁机车的牵引工况。当K1和K2掷于位置2时，流过电感Lf2的电流为负，被试机车输出制动能量，MLE模拟地铁机车的再生工况。调节S1和S2的占空比DS1和DS2即可改变机车牵引电流和制动电流的大小。

图1 MLE电路拓扑结构Fig.1 Topology of MLE circuit

1.2 电流解耦约束条件

在图1中设置二极管D1和D2，以保证MLE输入电流iLf1和输出电流iLf2解耦。除此之外，还需适当选择开关管S1与S2的开关时序进行配合。当S1和S2都导通时，D1关断，阻塞iLf2；S1和S2都断开时，D2关断，阻塞 iLf1；S1导通 S2断开时，D1和 D2均关断；S1断开S2导通时，因D1和D2均导通，iLf1和 iLf2之间出现干扰现象。

根据图1的电路结构，机车输入电压VAB、输出电压VCD与支撑电容两端电压VC1、开关管S1占空比DS1与开关管S2占空比DS2之间的关系为

MLE要满足输入电压近似等于输出电压等条件，即 VAB≈VCD、VC1≥2VAB，所以

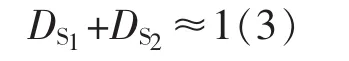
故S1与S2的占空比满足开关频率相同，且DS1≥0.5，DS2≤0.5，可避免 iLf1和 iLf2相互干扰。S2的开关时序有两种方案，如图2所示。①S1开通，S2同步导通，即如S21所示；②S2关断，S1同步关断，即如S22所示。K1和K2的作用是切换MLE工况，如牵引工况切换至再生工况，K1和K2同时动作1次，与S1和S2的开关时序没有明显联系，故无需考虑K1和K2对S1与S2开关时序的影响。考虑到MLE硬件实验编程语言的简洁性，选择第1种开关管占空比控制方案。

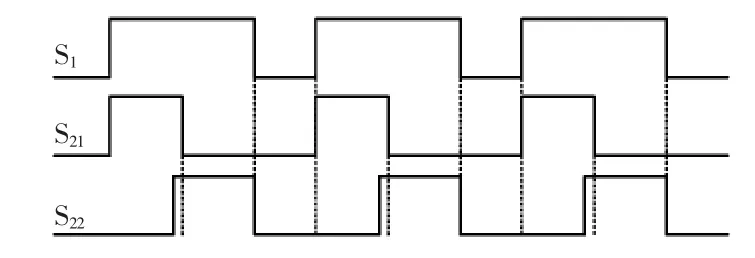
图2 开关管S1与S2开关时序Fig.2 Switching sequences of S1and S2

根据上述约束条件，分析不同开关占空比情况下，流过二极管D1与D2的电流iD1与iD2，波形如图3所示。由图3可知，只有在满足前述约束条件的情况下，电流iD1与iD2之间才不存在干扰现象，MLE输入与输出电流解耦。

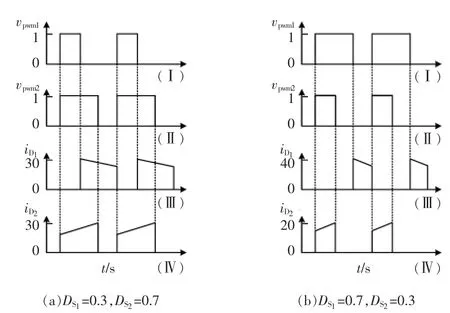
图3 二极管D1、D2电流波形Fig.3 Waveforms of current in diodes D1and D2

1.3 控制方案

MLE拓扑是由两个直流变换器级联组成，要求牵引工况输入功率与再生工况输出功率可控，所以控制方案采用不互相干扰的单独闭环控制：即电压闭环与电流闭环。控制方案示意如图4所示。

电压闭环控制方案采集支撑电容电压vC1作反馈量，用以控制开关管S1的占空比DS1变化。若vC1大于期望值 vC1_ref，vC1采样值vC1_cy与vC1_ref做差后得到的差值为负。差值经过PI调节器后，得到调制波与载波进行比较，输出的PWM信号占空比DS1会比之前有所下降，但不会小于50%。从而使vC1降低到参考值附近，动态调节实现闭环控制。

电流闭环控制方案采集流过电感Lf1的电流iLf1作反馈量，用以控制开关管S2的占空比变化。若iLf1小于期望值iLf1_ref，iLf1采样值iLf1_cy与iLf1_ref做差后得到的差值为正。差值经过PI调节器后，得到调制波与载波进行比较，输出的PWM信号占空比DS2会比之前有所增加，但不会大于50%。根据上文得到的iLf1与iLf2的关系式，改变iLf2的大小即可改变iLf1的大小，使iLf1升高到参考值附近，实现闭环控制。

图4 MLE控制方案示意Fig.4 Schematic of MLE control scheme

2 模拟系统结构及能量回馈分析

图5（a）为MLE处于牵引工况时，模拟系统的拓扑结构示意。其中Rq为接触轨（也称“第三轨”）阻抗，Rz为走行轨阻抗，回馈线路连接至牵引所a/b的正负极端。系统的能量流动情况如图5（b）所示。被试机车从接触轨获得牵引能量Pqy1和Pqy2后，由于自身没有能量存储装置，除去自身损耗的剩余能量Pfb1与Pfb2，通过陪试机车分别回馈给牵引所a/b。但牵引所能量只能输出，所以回馈能量最终汇入接触轨与走行轨，供被试机车牵引启动。

图5 模拟系统结构与能量流示意Fig.5 Schematic of the simulation system’s structure and energy flow

不考虑线路损耗，对接触轨能量状态进行分析：接触轨以iLf1输出能量给被试机车；陪试机车以iLb1和ifb2回馈能量给牵引所a/b；牵引所a/b分别以i1和i2提供能量给接触轨。根据一个开关周期电荷守恒的原则，得

其中：ifb=ifb1+ifb2，i=i1+i2。因 ifb、iLf1、i均为直流量，忽略纹波，得到

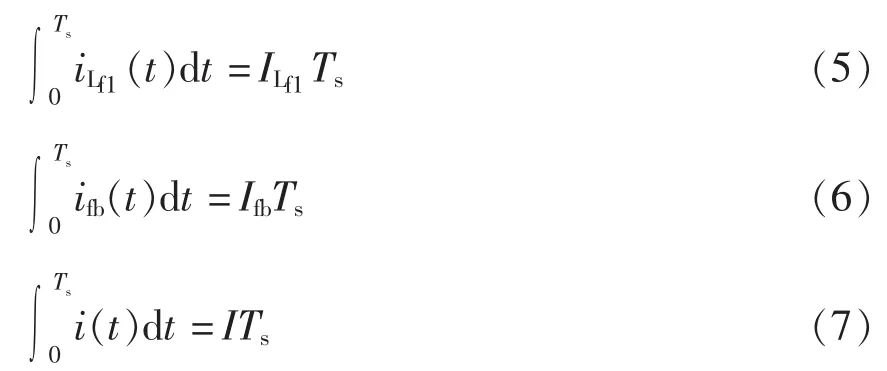
将式（5）～式（7）代入式（4），得到回馈电流平均值Ifb与MLE输入电流平均值ILf1的关系，即

根据MLE的结构特点，回馈电流与系统输出电流相等，即ifb=iLf2。结合式（8）知：牵引所a/b提供MLE自身损耗的能量，但接触轨中流动的能量仍为被试机车所需的牵引能量，主要由回馈能量提供。

当MLE处于再生工况时，机车运行方向与牵引工况时相反；所以图5中AB两点应分别接至正馈线与负馈线，CD两点分别接至接触轨与走行轨。此时，陪试机车通过电感Lf1回馈再生制动能量，接触轨电压上升，通过被试机车消耗回馈能量，以平衡接触轨电压，避免再生失效。

不考虑线路损耗，分析接触轨的能量状态。陪试机车以ifb1和ifb2回馈能量给牵引所a/b；接触轨以iLf2输出能量给被试机车；牵引所a/b分别以i1和i2提供能量给接触轨。与牵引工况分析类似，得

回馈电流与系统输出电流相等，即ifb=iLf1。所以牵引所a/b同样提供MLE自身损耗的能量，再生制动能量主要通过被试机车牵引启动消耗。由此可知，本文提出的模拟系统能够实现在实验室条件下模拟地铁牵引供电系统以及机车的典型工况，同时实现地铁机车的能量回馈。回馈电流大小近似等于模拟系统的输出电流,不需要实验室电源提供机车额定功率，只提供MLE损耗即可。

3 模拟系统仿真结果及分析讨论

为进一步验证上述理论的正确性，对图5电路进行仿真，参数设置如表1所示。VDC1、VDC2分别是牵引所a与牵引所b输出电压，Lf1、Lf2是MLE的电感，C1是MLE的支撑电容，DS1是MLE开关S1的额定占空比，DS2是开关S2的额定占空比，fs是开关S1与S2的开关频率，Rq为接触轨总阻抗，Rh为负电压回流线总阻抗，Rz为走行轨总阻抗。

表1 模拟系统参数Tab.1 Parameters of simulation system

3.1 仿真结果

在模拟系统中，被试机车的额定功率设为2 MW，对应系统输入电流为2 667 A。t1=1 s至t2=7.5 s，被试机车从牵引所与陪试机车汲取能量，一直运行在牵引工况；t2=7.5 s至t3=12 s，被试机车的牵引电流很小，处于惰行状态；t3=12 s至t4=18 s，被试机车输出能量至回馈线路，故一直运行在再生工况。

仿真结果如图6所示，牵引工况时，被试机车输入电流平均值ILf1是2 666 A，输入电压平均值VAB为697 V，输入功率为1 860 kW。陪试机车输出电流平均值ILf2是2 410 A，输出电压平均值VCD为750 V，输出功率为1 810 kW。系统中开关器件与元件寄生参数产生的功率损耗，即为输入功率与输出功率之差50 kW。此工况中，回馈输出端电压即为陪试机车输出电压，回馈接收端电压即为被试机车输入电压，回馈电流是陪试机车输出电流，由此计算可知回馈效率为93%。

再生工况时，陪试机车输出电流平均值ILf1为-2 667 A，输出电压平均值VAB为750 V，输出功率为2 MW。被试机车输入电流平均值ILf2为-2 986 A，输入电压平均值VCD为714 V，输入功率为2 130 kW，系统同样产生开关损耗与ESR损耗130 kW。此外，回馈输出端电压即为陪试机车输出电压，回馈接收端电压即为被试机车输入电压，回馈电流是陪试机车输出电流，由此计算知回馈效率为95%。整个工作过程中，被试机车两端电压VAB与VCD理应近似等于牵引所输出电压750 V，但由于损耗的存在与牵引启动过程造成的电压跌落，使得两电压均与额定值有一定差距，但其依然在500～900 V范围内，满足相关国家标准[13]的要求。

仿真结果与上述分析表明：模拟系统能够模拟实际地铁机车从牵引网取流的过程，也能够模拟能量注入牵引网完成制动的过程。此过程中，模拟系统将输出端能量回馈至输入端，实现能量回馈，验证了模拟系统理论分析的正确性。

图6 模拟系统仿真结果Fig.6 Simulation results of simulation system

3.2 分析讨论

前述仿真结果对2 MW功率等级的模拟系统进行了说明，此外，本文将不同功率等级的地铁机车输入电流、回馈电流和牵引所a/b输出电流的数据收集整理，对实验室进行地铁系统模拟实验时供电电源输出功率的要求进行探索。得到MLE不同功率等级（正功率为牵引工况，负功率为再生工况）情况下，输入电流-回馈电流关系曲线以及牵引所a/b输出电流随MLE输入功率变化的曲线图7所示。图7中，第Ⅰ象限曲线反应牵引工况时电流的变化情况，第Ⅲ象限曲线反应再生工况时电流的变化情况。

图7（a）是不同工况下的MLE输入电流-回馈电流关系曲线。对比曲线的走势与式（5）～式（14）知，曲线走势基本符合正比例函数的特点，所以能量回馈可以实现，前文有关模拟系统能量回馈过程的分析合理。图7（b）是模拟系统牵引所a/b输出电流i随MLE功率等级P变化的关系曲线。分析曲线的定点数据及变化趋势知，相同功率等级的情况下，牵引所a/b输出电流远小于MLE额定电流。若在实验室进行实验，实验室电源提供很小的稳态电流即可完成较大功率等级的实验。

图7 模拟系统相关关系曲线Fig.7 Related relationship curves of simulation system

本文提出的MLE不仅能够用于DC 750 V牵引供电系统，还能够应用在其他电压等级的牵引供电系统中。国际电工委员会拟订的3种电压标准是DC 600 V、DC 750 V和DC 1 500 V，我国标准规定2种[14-15]，为 DC 750 V 和 DC 1 500 V。在DC 1 500 V牵引供电系统中，供电系统结构等未发生变化，模拟系统的工作状态与能量流动情况与前文类似。

为验证分析的正确性，对DC 1 500 V模拟系统进行仿真，仿真结果如图8所示，MLE额定功率设为2 MW。由图可知，t1=5 s至t2=10 s，被试机车从牵引所与陪试机车汲取能量，运行在牵引工况；t2=10 s至t3=14 s，被试机车的牵引电流很小，处于惰行状态；t3=14 s至t4=22 s，被试机车回馈能量，运行在再生工况。综上所述，DC 1 500 V模拟系统能够实现地铁机车的典型工况与能量回馈过程，工作状态与前文所述DC 750 V模拟系统类似，模拟系统具有一定普适性。

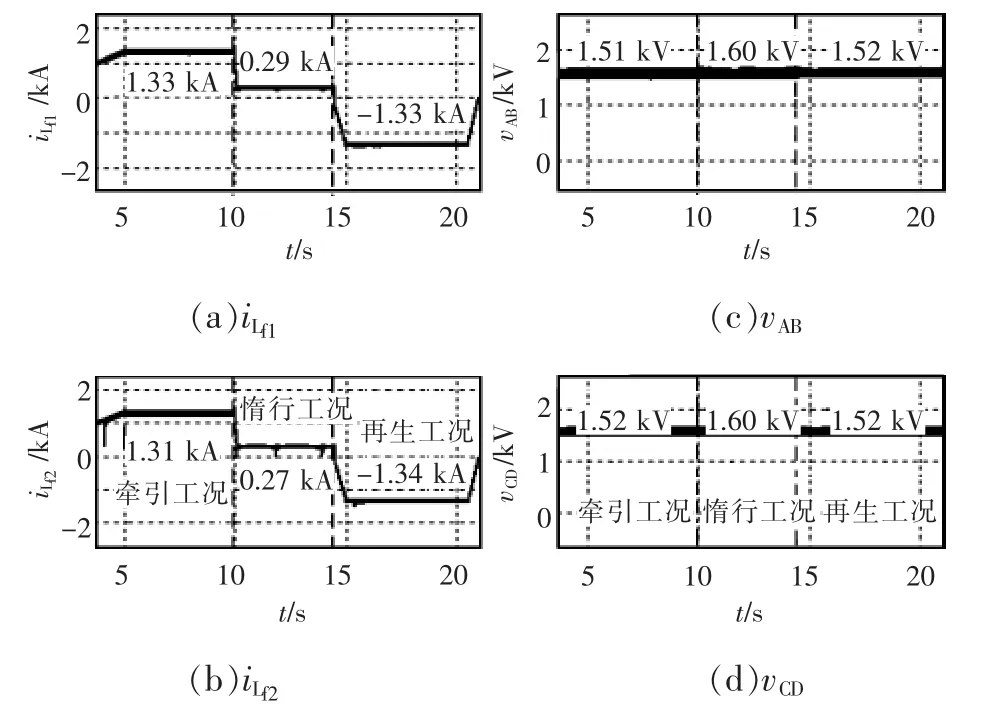
图8 DC 1 500 V牵引供电模拟系统仿真结果Fig.8 Simulation results of simulation system for DC 1 500 V traction power supply

3.3 电流解耦方案经济性分析

采用隔离变压器这一传统电流解耦方案的MLE拓扑结构如图9所示，接入牵引供电系统的方式与图1采用新型电流解耦方案的MLE类似。在相同外部输入特性的条件下，对两种解耦方案进行经济性比较，结果如表2所示。

结合图9、表2与上述分析可知，传统解耦方案需要1台变压器和8个开关管，而新型解耦方案只需要2个二极管，传统解耦方案的元件成本显然更高。为比较2种MLE的功率损耗和能量传输效率，对2种MLE拓扑进行仿真，仿真结果如图10所示。图1与图9 MLE输入电压（vAB=750 V）相同，输出端CD均接0.26 Ω纯阻性负载。

图9 传统MLE拓扑结构Fig.9 Topological structure of the traditional MLE

表2 不同电流解耦方式的经济性对比Tab.2 Comparison of economic efficiency between different current-decoupling methods

图10 传统MLE电流解耦方式仿真结果Fig.10 Simulation results using traditional MLE current-decoupling methods

传统解耦方案中，MLE的输出电压是730 V，开关损耗约20 V，能量传输效率约97%。新型解耦方案中，MLE的输出电压是740 V，开关损耗约10 V，能量传输效率近99%。综上所述，传统解耦方案开关器件数目多，开关损耗升高，影响能量传输效率，且控制策略较复杂，可靠性相对较低。新型解耦方案因避免使用高频隔离变压器并减少开关器件数目，在控制方式、功率损耗、元件成本以及能量传输效率等方面都具有一定的优势。

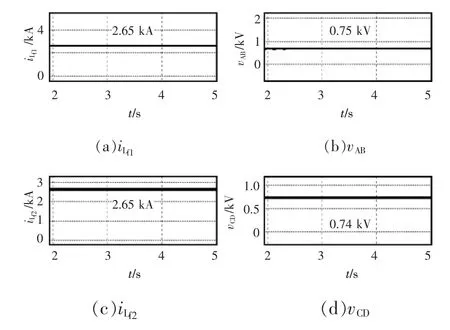
图11 新型MLE电流解耦方式仿真结果Fig.11 Simulation results using novel MLE currentdecoupling methods

4 结语

本文提出非隔离型地铁机车工况模拟能量回馈系统，并对其工作原理与能量回馈过程进行了详细推导与分析。仿真结果表明，本文提出的模拟系统通过在升压单元与降压单元级联结构负电位线不同位置串入2个二极管后，结合占空比控制策略，即实现了MLE输入电流与输出电流解耦，能够在DC 750 V和DC 1 500 V牵引供电系统中正常模拟地铁机车典型工况与能量回馈过程；而且，与采用隔离变压器的传统电流解耦方式相比，本文采用的电流解耦方法在器件成本、控制方式与能量回馈效率等方面具有一定优势。若将本文提出的模拟系统硬件化，并在实验室进行实验，模拟牵引所的电源提供机车的损耗电流即可，对电源输出电流要求较低。此外，本文提出的模拟系统具有一定普适性，适用于多种直流牵引供电系统模拟。