高中数学易错点指导方法举例

朱玲玉

(江苏省平潮高级中学 226361)

一、概念失真导致的易错点

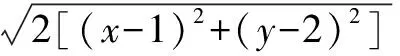
当提供问题之后，教师应当与学生进行分析：上述两个问题，重点对圆锥曲线的不同定义进行考查，解决此类问题的关键点在于真正理解并掌握定义的内涵，其中在圆锥曲线的第一定义里面，对于两定点间的距离和与正常数大小关系进行限制，而第二定义里面则提出定点位于定直线之外的要求，这些容易为学生所忽视，却恰恰又容易出现在考查内容之中，因此需要格外留意.

二、主客混淆导致的易错点

在高中数学问题中，还易于同时出现多个字母，因此有必要使学生明确这些字母的含义，了解何者为主元，何者为参数，否则便会发生认识方面的偏差，导致解题的错误.若是不同字母在地位上是均等的，则可以利用主动设定主元的帮助，强化对于认知结构特点的了解，从而将处理问题切入点变得更加清晰，有些问题还可以采取反客为主的形式，使复杂问题简单化，像下面的问题：

如果不等式lg2x-(m+2)lgx+m-1>0对于 |m|≤1恒成立，那么x取值范围为 .

当提供问题之后，教师应当与学生进行分析：在此不等式之内包含了两个字母，如果依照定势思维，则会认为此不等式直接关联于字母x，造成主、客混淆的认知错误，直接依二次函数性质对问题进行处理，得到的结果也必然无法正确.事实上，在本题之中，其主元为m，x为参数，因此需要借助一次函数图象以及性质，对不等关系进行列出，由此让问题得到顺利处理.

三、隐含信息遗漏导致的易错点

高中数学问题的处理过程，实际上也是矛盾进行相互转化的过程，在此过程中，将已经清晰的条件充分利用起来，并借此深入挖掘表象之下所隐含的信息内容，做到条件与结论的充分联系，顺利处理未知问题.隐含信息遗漏导致的易错点具体体现于下述几个方面.

其二是没有明确题目中所隐含的关键字，例如：已经知道命题“四边相等的四边形为正方形”，那么该命题的否定为____.

这个问题便隐含了关键字，如果不进行深入挖掘则极易出错.命题和命题之否定属于相互对立的，原命题为假命题，若是不经认真思考，极易将其否定错写为“四边相等的四边形不为正方形”，与原命题对立的命题也为假命题，这不符合常理，因此需要探索出问题之中的隐含关键字，四边相等的四边形“都”为正方形，得到其否定形式：四边相等的四边形“不都”为正方形.

其三是没有明确数量关系之中所隐含的一些几何特征，因此导致解题过程中无法比较顺畅地进行相互转化，无形中增加了运算量，很多时候都会造成实际结果与正确结果之间的差距.特别是在高中数学学习过程中，一定要对常见的几何特征和几何量，比如距离、函数图象轴对称性以及凸凹性等量化形式加以认知.例如下面的例子：(1)如果不等式|x-1|+|x+2|>m对任何实数x恒成立，那么m的取值范围为____；(2)若函数f(x)=x2+bx+c对任意实数t均有f(2+t)=f(2-t)，那么可以知道 ，A.f(2)

易错点的展示是对传统数学教学方法的一种必然补充，因为新课程改革持续走向深入，它的应用频率也明显增加，因其能够站在不同视角对各种类型知识点进行示范讲解，所以可以更有效带动学生的数学思维特别是实际处理问题能力使之得到强化.实际操作过程中，高中数学教师在给学生提供数学知识点的教学内容之际，可以从概念失真、主客混淆、隐含信息遗漏等角度出发，使学生主动投入到有关知识内容的探讨中来.