抛物线焦点弦问题的多解探究

李欣泽

(天津市实验中学滨海学校高三年级 300450)

进入高二年级开始了解析几何的学习，教学中老师的奇思妙解深深吸引了我，更激发了我对解析几何的浓厚兴趣，以下是我对一道解析几何题的多解探究.

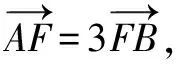
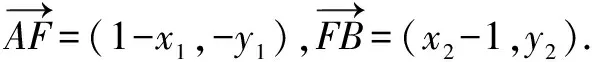
∴1-x1=3(x2-1),-y1=3y2①.

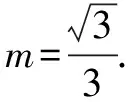
思路小结通过代数方法解决几何问题，体现了解析几何的特征，是一种很基本的解题思想.

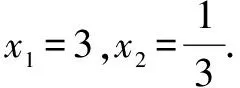
思路小结解法二充分体现了定义和向量坐标运算的结合.

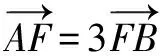
思路小结解析几何有非常多的结论，如能巧妙运用之定会使问题变得非常清晰明朗！

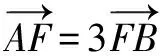
思路小结这种方法告诉我们抛物线方程也可以作为一个条件，我们不能只看到两者之间的几何关系，一定要善于利用方程解题，这一思路在椭圆双曲线中也都可以使用.

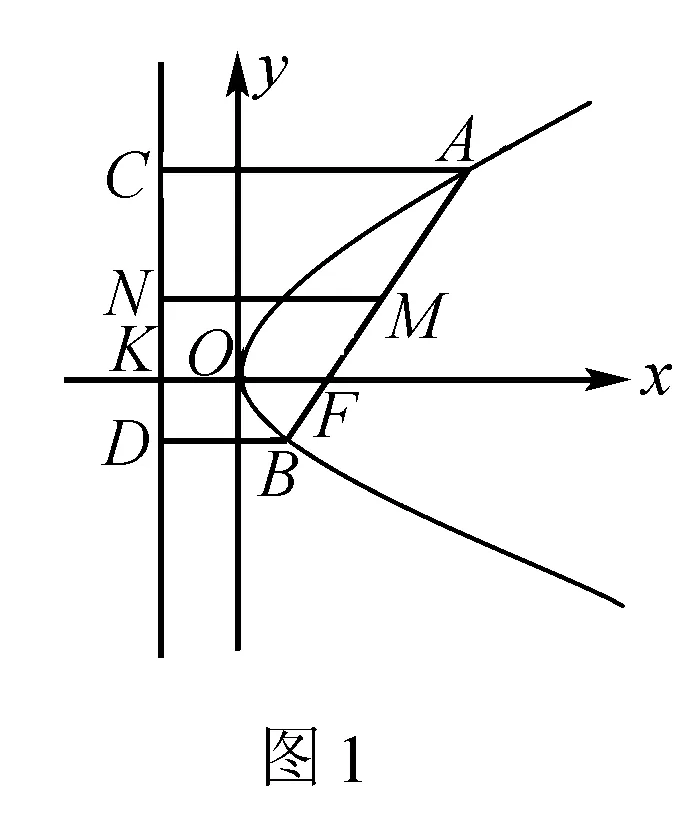
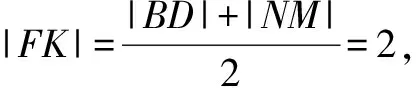
思路总结这种方法非常好的利用了图形中的平行和比例关系，体现出了解析几何的“平面几何”特征.

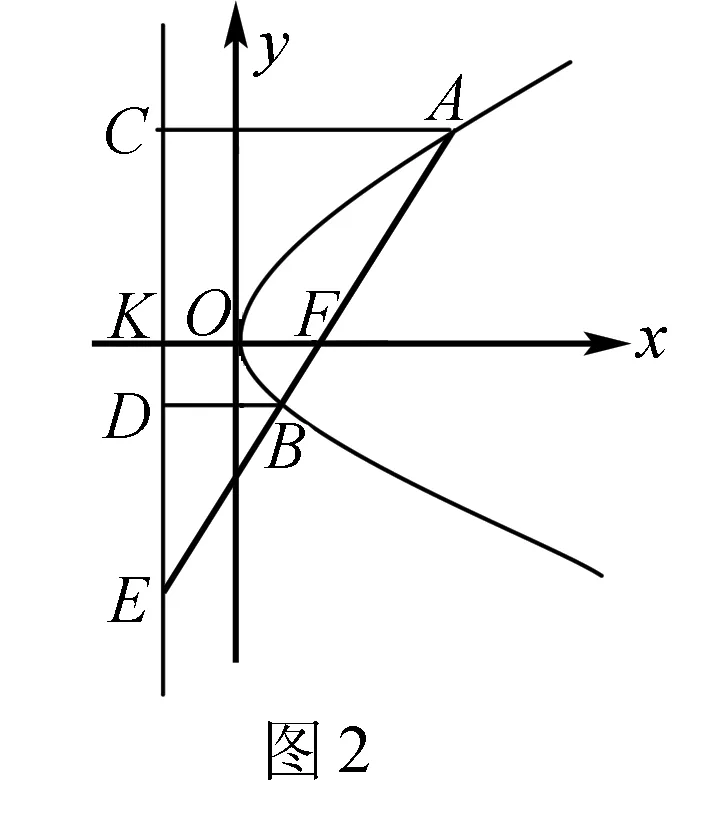
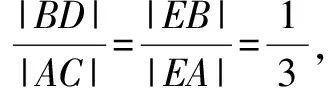
以下有两种思路，一种思路结合计算可得KF为三角形ACE中位线，从而问题得解.

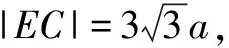
思路总结第一种思路也体现了解析几何的“几何”特征.第二种思路体现出了用几何图形求直线斜率，是我们解决解析问题方法的补充.

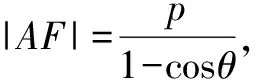
思路总结合理的运用焦半径公式会使得问题难度明显下降，让问题迎刃而解！

总评这是一道典型的焦点弦问题，它的求解过程充分体现了解析几何的解题特点——既可以采用代数方法求解也可以结合平面几何知识，如能将两者结合采用数形结合的方法则求解会变得更加完美.

课下练习直线l∶y=k(x-2)(k>0)与抛物线C:y2=8x交于A,B两点，F为抛物线C的焦点，若|AF|=2|FB|,则k的值是____.