一题多解与一题多变在高中数学学习中的运用

徐 臻

(甘肃省张掖市高台县第一中学高二7班 734300)

一、一题多解在高中数学学习中的应用和效果

在新课标和素质教育的理念下，学生是课堂学习的主体，教师在课堂教学中只扮演着引导的作用.在高中阶段，我们的学习能力和智力发生着巨大的变化，每个学生的数学基础知识和思维方式都有着很大的不同.因此，在解决实际问题时，一个解决问题的方法不一定适用于每个学生.因此，在我们进行主动学习的过程中，应该对问题多加研究，从中找到适合我们自己思维模式的解题方式.

实践证明，数学公式在解决数学问题中起着非常重要的作用.要学习数学，我们必须掌握数学公式并加以应用.然而，大多数同学都倾向于完全地学习公式，他们对公式的推导并没有给予足够的重视，甚至忽略了公式的推导.从本质上讲，推导公式是一种解决问题的方法，或者是一种可以一目了然的解决问题的技巧.将一题多解应用于公式的推导过程中，可以使学生更好地理解公式和概念，同时也能加深学生对一题多解的理解.随着时间的推移，我们就能够逐渐形成一题多解的思维，在学习中也能更多地应用一题多解的方法，潜移默化地培养学生的数学思维、逻辑思维以及创新思维.下面将给出一个具体的例子来探究一题多解.

这一题就可以充分地应用一题多解的方法.

方法四：判别式，将函数化为有x2-xy+1=0,Δ=y2-4≥0,所以y≥2，所以函数的值域是[2，+∞).

二、一题多变在高中数学中的应用和效果

在高中数学学习中，我们可以通过对知识的理解进行有效的题目变形从而培养学生的实践探究能力.为了提高课堂学习的效率，通过合理问题的转变，使问题的类型不断深化，将一道题演变成不同类型的题目.

一题多变，对于一个数学问题进行有效的类比、联想和发散，我们可以得到一系列的新题型，甚至得到一个不一样的结论，同时对这些新的题目进行解答，即使它最终没有得到解决，也可以尝试去解决它.这样可以更好地培养我们的创新能力，在能力和形式上逐步发展发散思维，提高我们的发散思维，培养我们的解题思维和能力.

从特殊性中逐步提升的思维过程有助于培养我们的思维能力.用一题多解和一题多变可以培养我们的综合能力、逻辑思维以及创新思维.充分挖掘经典案例，注重改变题目类型，不仅可以掌握基础知识，还可以激发我们对知识的追求欲，提高创新能力.这有助于进一步提高我们数学思维能力和数学学习兴趣，以便应对多变化的数学题型.

三角函数知识在高中占据的比重是很大的，一般是对三角函数进行化简、降幂等处理，来解决相关的问题，下面就以三角函数为例，来具体的探究一题多变.

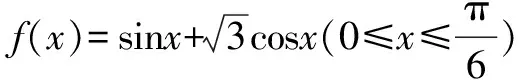
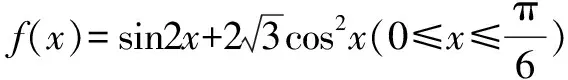
这几个例题都是由一个简单的例子而来的，通过对这几个例子的解答和探究，可以更好地培养我们的三角函数的知识，同时也能加深我们对三角函数知识的理解和应用.上面几个例子都是由简到难演变的，同时这几个例题都是有解的，使得对这几个例子的探究更有意义.同时在这几个例子的解答过程中也可能进行一题多解，有效地培养我们的数学思维、逻辑思维以及创新思维.

一题多解和一题多变是数学学习中重要的一种方法和手段，它们不但能培养我们对相关知识的学习，还能够在一定程度上培养我们的解题能力和技巧，使我们的思维得到升华，使我们的逻辑思维、创新思维得到培养，使我们都能通过学习来找到属于我们自己的解题方式和解题思维.