二项式定理教学探究——从知识的形成过程诠释计数原理

姚 刚

(浙江省宁波外国语学校 315211)

一、 问题引入，激发学生兴趣

引入：二项式定理研究的是什么？研究：(a+b)2=a2+2ab+b2，(a+b)3=?(a+b)4=? (a+b)5=?

问题1：展开上述表达式，展开式各有多少项？系数是多少？(学生动笔展开表达式)

问题2：感受系数与什么数相关？排列数？组合数？(引导学生思考方向)

问题3：二项式定理仅仅研究这几个式子吗？(a+b)100=? 那么(a+b)n的展开式又是什么？

笔者的用意是以问题链的形式作为教学的起点，直接给出本节课需要解决的问题，同时板书展开式各项系数时，以杨辉三角的结构书写，观察系数的特点；

二、通过对(a+b)3的再次分析，引出计数模型

学生在展开过程中窃窃私语，觉得n慢慢变大时，展开越来越繁琐，那么如何比较简捷地求出系数呢？激发学生学习兴趣.学生通过观察发现：

(1)n=4、5的系数与n=3的系数有递推的联系；

(2)系数与我们的组合数有一定的联系.

引导学生从组合数的角度与尝试解释，笔者又给出了第一个探究以及问题链：

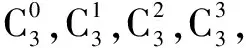
问题1：如何展开(a+b)3？a3如何来？项如何产生？

板书：(a+b)3=(a+b)(a+b)(a+b) =(a·a+a·b+b·a+b·b)(a+b)=a·a·a+a·b·a+b·a·a+b·b·a+a·a·b+a·b·b+b·a·b+b·b·b=a3+3a2b+3ab2+b3.

笔者板书一步一步展开，意图让学生感受项的产生过程，感受组合在展开过程的作用.

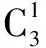
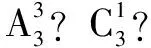
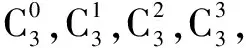
三、 由特殊到一般归纳出定理

同学们分组讨论，通过对计数模型的讨论，得出n=4、5其实不需要繁琐计算就可以得出系数，笔者趁热打铁，又给出了第二个探究：推广到一般结论

探究2：根据上述过程，请你推导(a+b)n展开式中有哪些项？系数是多少？

根据(a+b)3的展开原理不难发现(a+b)n中的项为：

an，an-1b，an-2b2，…，an-kbk，…，abn-1，bn，

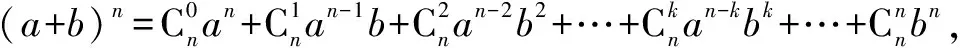
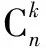
教师指出：二项式定理就是我们计数模型的运用，从中告诉学生，我们计数原理是很有用的，而且身边随处可见，然后由学生总结出二项式定理的公式特征：

项数有n+1项；

次数和为n次，按b的升次或a的降次排列；

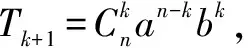
最后反思：通过本次教学，让学生体会了整个探索过程，找到科学探索的一般规律：先找到特殊例子，再观察特殊例子中的规律，形成不完全归纳、猜想，然后再去试图证明或否定这些猜想，这对学生数学能力的提高非常重要，本节课有两处归纳：

(1)发现n=3，n=4，n=5，…的系数有联系，后续可以用数学归纳法证明;

(2)发现系数都是组合数,然后，根据这些猜想尝试证明，挖掘出了其蕴含的内涵，得到了二项式定理.

但是很多时候我们忽略这些定理、公式最初发现所受到的艰辛历程，再加上，传统的教学比较重结果，轻过程，重应用，轻探究，从而导致我们学生看不到原理的生成，使学生对数学产生了一种数学难的想法，这绝对是我们不希望看到的.

教学过程中知识的运用固然重要，但是凸显数学的本质才是关键，我们不必急于对知识进行机械的训练，而应追求水到渠成的教学效果，只有这样，才能增强学生的学习能力，提高学生综合素质，才能真正体现高中数学课程标准的理念.