基于题根研究下的函数与导数问题

王永亮

(山东莒县第一中学 276500)

一、我国高中数学中导数与函数教学难点

1.教学模式结构单一

首先，我国大部分高中学生都处于文理科分科的形式中.虽然高中数学仍属于文理科中的重点教学课程，但由于大部分文科生将自身学习重点仍旧放在文科课程中，认为数学知识对自己日后的文科学习并无多大帮助，在学习过程中产生携带性能力，无法对数学中的导数与函数知识重点进行掌握；其次，由于部分文科生在分科之后，大部分教师的重点都放在文科课程中，甚至部分数学教师自身对教学目标与内容的意识也产生偏差，导致部分文科学生的数学课堂常出现被占用的情况，而学生无法获取更多知识，导致在解答函数与导数以及其他方面的数学题目时出现较多错误，而学生自身数学能力无法得到提升，导致数学课程失去作用；第三，传统高中数学教学过程中，教师是占据课堂的主体，而学生则常作为课堂辅助形式存在，教师通过长篇阔谈的方式对数学函数与导数知识进行讲解，而学生则需要对公式进行死记硬背，利用套用等方式对导数与函数的题目进行解答，虽然能够对教师当时讲述的东西进行模仿，但却无法做到举一反三，导致学习结构单一化，同时也使学生在挫败中失去对数学知识学习的兴趣，对导数与函数之后的教学开展产生不利.

2.导数与函数的表现形式复杂多变

函数形式本就复杂多样，并不具备统一形式，而其中所包含的区间、不等式以及其他概念也均不具备某一种固定值或概念，而在利用导数对函数进行求解时也无法遵循统一模式，由此可见，函数与导数存在较强的抽象性、模糊性.而数学教师在利用传统教学方法对这一部分内容进行讲解时，虽然能利用宏观概念使学生初步了解导数与函数的基本含义，但在具体学习的过程中仍旧会因导数与函数表现出来的复杂性、多样性弄昏头脑，无法充分利用自身所学知识提升函数与导数的做题效率，无法做到灵活应变.此外，由于导数与函数中存在各类代替未知数字的符号，而每个符号的意义不同，在部分函数与导数中所代表的内容也十分复杂，虽然有一部分先天智力较高的学生能够将所学到的知识融会贯通，但大部分学生仍旧处于模糊状态，而教师无法利用现有教学方式改善这一现象，导致教学出现较大问题.

3.导数与函数的数形转换难度较大

上述中提到，高中导数与函数类型题目在解答过程中具有较多符号，而学生在进行解题时虽掌握了基本解题理念，因无法根据题目内容及问题重点对数学符号及相关数据进行图形转换，无法将所学知识灵活运用，导致数形转换过程存在困难，使学生解题难度大幅度增加.而部分学生虽然对教师讲述的内容进行记忆，但由于他们只是机械地将教师讲述内容记住而已，却在解题或之后的学习中无法利用记忆中的内容进行学习，因此这些学生表面上看起来学习认真，但实际上却缺乏分析能力，无法在解题时继续进行数形转换，而教师对学生的批评也使学生逐渐失去信心，逐渐对高中数学内容产生排斥心理，直到放弃数学，导致学生最终在日后的学习及高考中增大了数学带来的压力.

二、题根式教学概念及作用

题根式教学是由我国陕西师范大学罗增儒教授提出的新概念.罗教授在对基于新课程的数学解题教学进行讲解与分析中提到，可以利用题根式教学对当下数学解题困难的现状进行改善.罗教授指出，虽然现如今使用的变式教学包含具有科学性与广泛性的数据库，但由于数据库本身就是一个较为宏观的存在，而高中数学能够运用的内容极为有限，如果全靠变式教学根本无法发挥数据库自身的优势.而为了实现新课程中高中教学目标内容，如果利用题根式教学代替部分变式教学，并将其逐渐发展为主流教学方式，则能够使教学效果更加明显.

当下我国高中数学教学形式极为严峻，虽然新课改提出有关高中数学教学的目标，但从根本上来看，传统教学方法已经无法满足现代教学思想与教学内容，同时也无法提升学生学习能力，而利用题根解题的思想及题根式教学法对现有数学教学加以改善，利用题根寻找出学生在学习中最难解决问题，并面向数学核心知识开展教学，使题根式成为数学教学中最具高效性、灵活性的教学模式，从而达到提升我国高中数学教学水平的效果.

三、基于题根研究下的导数与函数问题分析

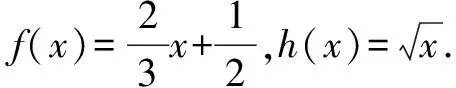
(1)设函数F(x)=18f(x)-x2[h(x)]2，求F(x)的单调区间与极值；

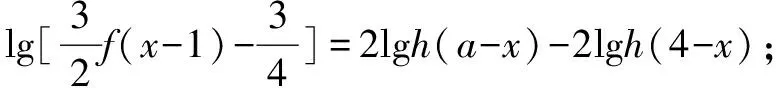
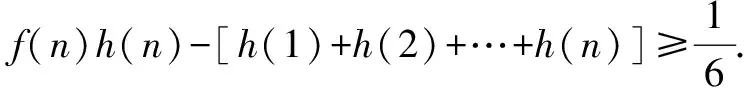
在对本题进行解答时，首先教师可通过结合相关函数与导数概念对题目进行分析，并由学生从题目中寻找题根.已知本体题根有四个，而为了更为简便地得到正确答案，数学教师应当引导学生根据函数已知方程进行数形转换，而在转换过程中，教师应当注意每一位学生的状态与转换思路，如果发现有学生转换错误也不要批评，以免对学生的自信造成打击.

得出转换图形后，教师需要引导学生充分对题根进行分析，并根据分析结果对题目和得到的转换图形加以推算，最终将本题解答出来.

解原方程可化为：

log4(x-1)+log2[h(4-x)]=log2[h(a-x)],

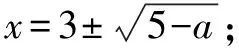
当a=5时，原方程有一解x=3；

当a≤1或a>5时，原方程无解.

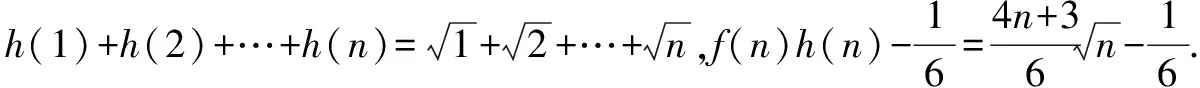
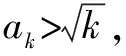
则Sn≥h(1)+h(2)+…+h(n)，故原不等式成立.

本次解题不仅是对学生数形转换、函数与方程、导数运算、分析以及解题等能力的考查，同时也是提升学生题根解题概念的重要依据，为之后学生的解题与题根式思维水平的提升奠定基础.

例2 设函数f(x)=a2lnx-x2+ax,a>0.

(1)求f(x)的单调区间;

(2)求所有实数a，使e-1≤f(x)对x∈[1,e]恒成立.

注：e为自然数的底数.

(1)解因为f(x)=a2lnx-x2+ax,其中x>0,

由于a>0，所以f(x)的递增区间为(0，a)，减区间为(a，+∞).

(2)证明：由题意得，f(1)=a-1≥c-1，即a≥c。

由(1)知f(x)在[1，e]内单调递增，

要使e-1≤f(x)对x∈[1,e]恒成立，

本题主要考查学生在利用导数在函数单调区间内进行求值范围的能力，通过引导学生结合导数运算法则及其他基础知识，在完成对学生的抽查的同时全面提升对学生现有学习能力的了解，而教师则需要结合现有教学法和题根教学法，利用科学理念加强对全体学生的教学，提升学生数学能力，达到完善数学教学的目的.