浅析高中数学学习中如何运用函数与方程思想

赵肖亚

(山东省聊城市莘县第一中学56级17班 252400)

高中数学知识中涉及到大量的数量关系，复杂的变化关系，这就要求我们在学习的过程中，能够理清数学中的各种关系，通过构造函数或方程来进行这些数学问题的探究，往往能抓住问题的本质，将看似纷繁复杂的问题变得具体化、简单化，从而有效的解决问题，掌握知识，提高学习效率.

一、函数与方程思想概述

函数与方程之间有着密切的关系，是进行高中数学知识学习的重要思想，在数学知识深入探究、数学问题解决、生活实际现象建模等方面都有着重要的应用.因此，掌握函数与方程思想，对于促进我们的学习积极性，提高我们的学习效率具有关键性的作用.就函数与方程思想的内容与作用来说，函数与方程思想可以将初高中的有关函数与方程的知识衔接起来，进行有关最值、不等式、方程(组)、单调性、值域等问题的分析与解答，并且可以帮助我们将具体的问题构造成函数或方程，将实际问题转化为数学问题，从而更有利于我们对数学问题进行化简，提高解题效率.

二、函数与方程思想的运用策略

函数与方程思想在高中数学问题解决中有着广泛的应用，同时也是高考的热点内容，掌握函数与方程思想不仅能提高我们的自主学习效率，也能让我们更深入地理解数学的内涵，掌握数学的规律，从而对数学问题能够进行有效地解决.

1.不等式问题中函数与方程思想的运用

函数与方程思想是高中数学的灵魂，也是提高数学知识水平，掌握数学方法和技能的有效途径，在进行数学问题的分析中，数学思想可以给我们带来正确的指导思路.我们在学习的过程中掌握函数与方程思想，并在实际问题的解决中不断应用，可以活跃我们的思维，提高学习效率，掌握解题方法.

例1 如果a、b、c∈R，并且a、b、c满足以下关系：4a-4b+c>0，a+2b+c<0，那么可以得出( ).

A.b2≤acB.b2>acC.b2>ac，a>0 D.b2>ac，a<0

解析本题如果直接进行分析的话，基本上很难建立起已知条件与结论之间的关系，而通过对已知条件的观察，我们可以构建函数f(x)=ax2+bx+c，这个时候就可以通过函数将已知条件转化为f(-2)>0，f(1)<0，结合二次函数的图形，我们可以得出在(-2，1)的区间上，函数的图象与x轴有一个交点，这样就可以得出二次函数f(x)的图象与x轴有两个交点，则ax2+bx+c=0有两个实数根，从而通过Δ>0求出问题的答案B.

由此可见，在一些不等式问题的探究中，运用函数与方程思想，可以找出不等式之间的规律，从而运用函数与方程的一些性质进行问题的分析和解决，往往会起到意想不到的效果.

2.数列问题中函数与方程思想的运用

数列问题是高中数学知识的重要内容，同时也是高考考查的重点，一般解题思路是通过数列的性质和已知条件，列出方程(组)，从而通过解方程(组)的方式来求解数列，这样通过方程(组)将复杂的数列问题转化为方程问题，更有利于我们高效的研究.

例2 记Sn为等差数列{an}的前n项和．若a4+a5=24，S6=48，则{an}的公差为( ).

A.1 B.2 C.4 D.8

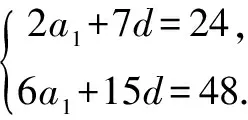
通过数学思想的运用，可以将一些未知的数学问题转化为已知的数学问题，从而有效地对问题进行解决.

3.三角函数问题中函数与方程思想的运用

三角函数公式一般比较复杂，在三角函数问题的分析中进行有关函数与方程思想的运用，可以让三角函数更加的直观和简单，通过函数和方程的一些性质进行问题的探究，更能提高探究的效率.

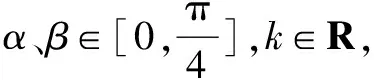
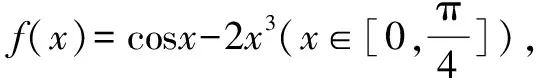
调递减性，可以得出α=2β，从而求得cos(α-2β)=1.

通过函数与方程思想的运用，可以将已知条件转化为函数，通过函数的单调性得到α、β的关系，从而将问题简化.

总之，函数与方程思想是进行高中知识学习的重要数学思想，涉及高中的许多知识，是研究高中数学问题的有效方法，巧妙地运用函数与方程思想，可以帮助我们将复杂的问题简化，将未知的问题已知化，从而提高学习效率，促进数学素养的形成，不断地提高我们的数学综合知识.