数形结合思想在高考导数问题的应用

边红霞

(河北省易县中学 074200)

数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事非.”纵观近几年的高考试题，用数形结合的思想方法解决抽象的数学问题，成为高考命题的热点.函数是考查数形结合思想的最好载体，特别是以函数与图象、曲线与方程、函数与不等式为模型，考查学生分析和解决问题的能力.使用数形结合的关键是“以形助数”，要做到“胸中有图，见数想图”，要善于发现条件的几何意义，刻画出相应的图形，还要根据图形的性质分析数学式的几何意义，这样才能巧妙地利用数形结合解决问题.

例(2016年全国新课标卷Ⅰ 理科数学第21题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)设x1,x2是f(x)的两个零点，证明：x1+x2<2.

解函数的零点是指函数图象与x轴交点的横坐标，确定方法是只要在区间(m,n)上满足f(m)f(n)<0，则在(m,n)上必存在x0，使得f(x0)=0.

(1)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).讨论：

①设a=0，则f(x)=(x-2)ex，f(x) 只有一个零点.

②设a>0，则当x∈(-∞,1)时f′(x)<0，当x∈(1,+∞)时，f′(x)>0，所以f(x)在(-∞,1)上单调递减，在(1,+∞)上单调递增，f(1)是其极小值，f(1)=-e,f(2)=a,所以在(1,2)上必有唯一零点.另一方面，如果在(-∞,1)上能够找到一个自变量b，使得f(b)>0即可.

③若a<0由f′(x)=0解得x=1或x=ln(-2a).

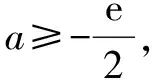
又当x≤1时，f(x)=(x-2)ex+a(x-1)2<0，所以f(x)不存在两个零点.

综上，a的取值范围是(0,+∞).

(2)因为函数有两个零点，因此a>0，此时由数形结合，不妨设x1f(2-x2)，即f(2-x2)<0.于是只证此式即可.由于f(2-x2)=-x2e2-x2+a(x2-1)2，为保持运算的一致：又f(x2)=(x2-2)ex2+a(x2-1)2=0即：a(x2-1)2=-(x2-2)ex2，所以f(2-x2)=-x2e2-x2-(x2-2)ex2,设g(x)=-xe2-x-(x-2)ex，则g′(x)=(x-1)(e2-x-ex)，所以当x>1时，g′(x)<0，函数g(x)在(1,+∞)上单调递减，而g(1)=0，故当x>1时，g(x)<0，从而g(x2)=f(2-x2)<0，故x1+x2<2.

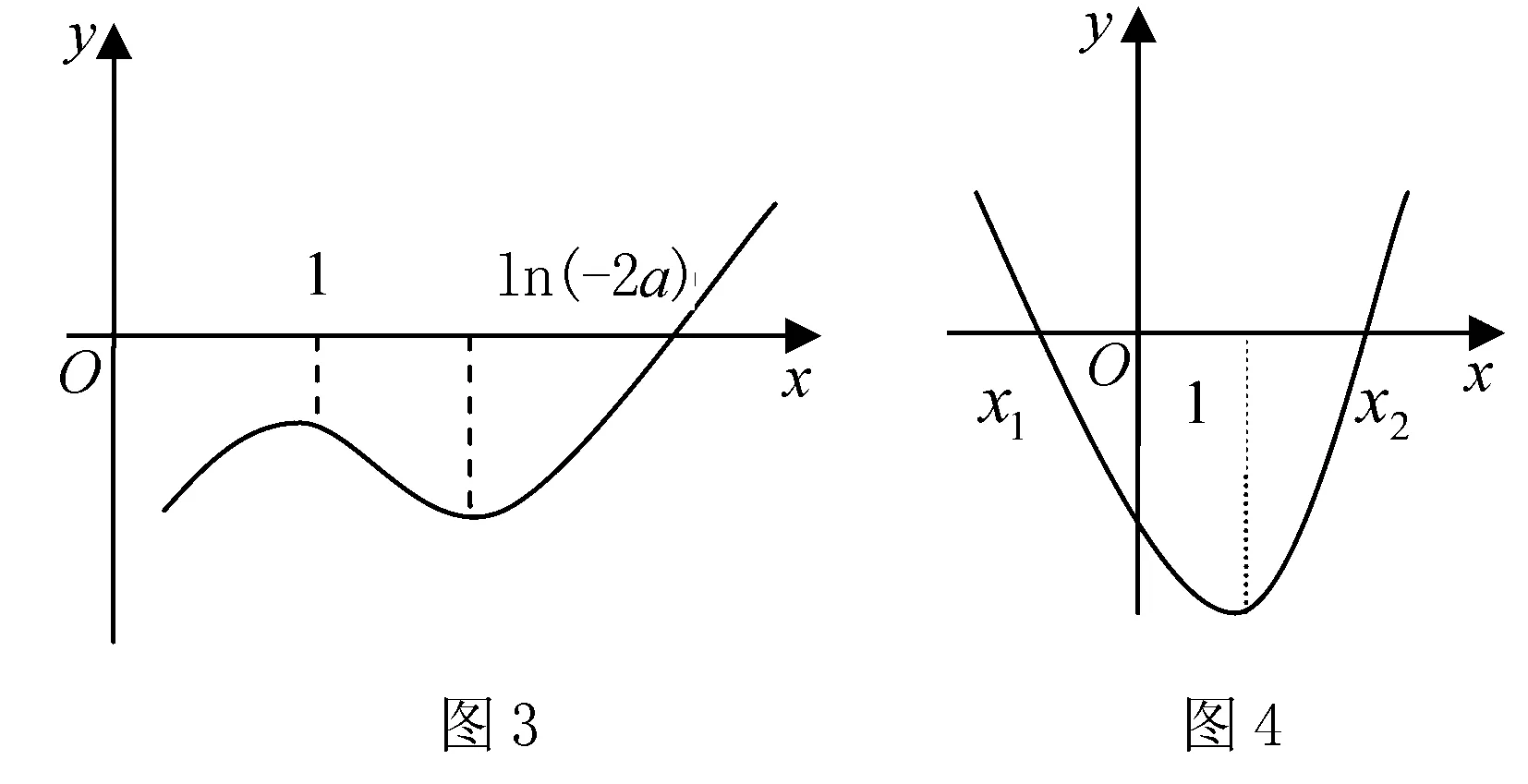
分析本题主要是考查导数的应用，在求解过程中考查数形结合思想、分类讨论思想、函数思想，考查运算求解能力及逻辑思维能力.此题充分利用数形结合，同时用了构造函数求极值，证明不等式，这是这道题目的最大亮点.

综上，数形结合是解决数学问题最重要的思想方法，特别是在高考导数题目中发挥着巨大作用.往往是在解决的全过程中，不断地通过数与形的结合，将抽象的问题具体化，通过图形找到解决问题的突破点，然后用数的推理去验证形的准确性，使解题过程达到顺畅通行！